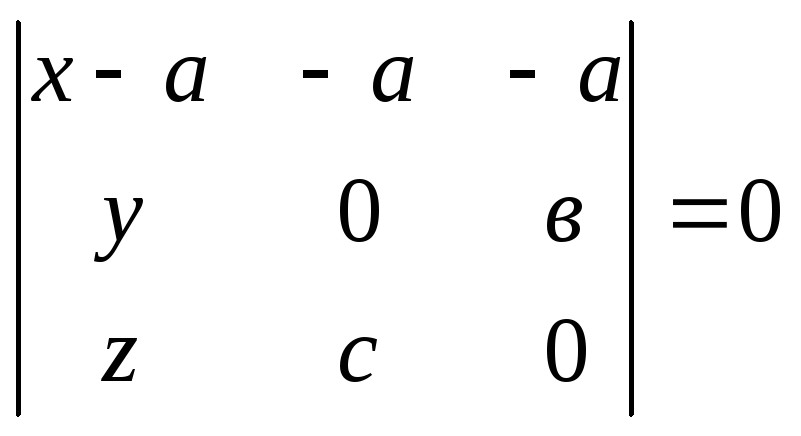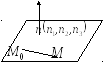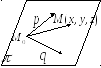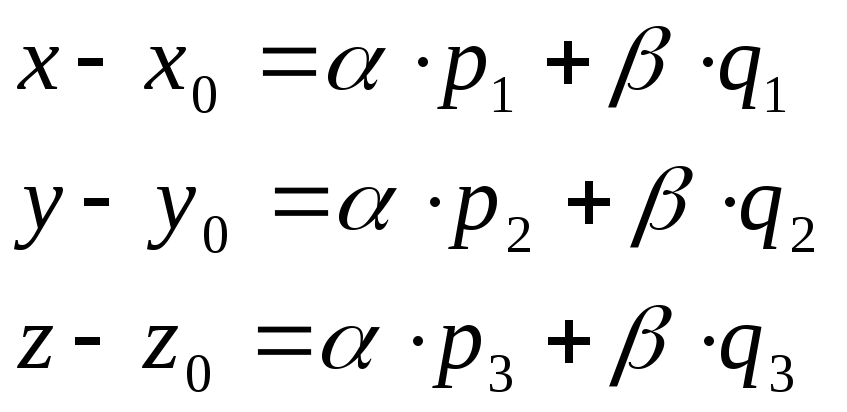Лекция №4
Плоскость в пространстве: способы задания плоскости, общее уравнение плоскости, геометрический смысл коэффициентов в общем уравнении плоскости,
геометрический
смысл знака многочлена
![]()
В некоторой аффинной системе координат для любой плоскости можно задать направляющее двухмерное подпространство.
Определение 4.1. Двухмерным подпространством L трёхмерного пространства V называется множество всех векторов, параллельных некоторой плоскости пространства V.
Определение 4.2. Направляющим подпространством называется подпространство, определяемое двумя неколлинеарными векторами.
Например, пространство можно считать заданным, если известны два неколлинеарных вектора, параллельных данной плоскости.
На плоскости
![]() с направляющим подпространством
с направляющим подпространством
![]() рассмотрим некоторую точку
рассмотрим некоторую точку
![]() .
Точка
.
Точка
![]() лежит в плоскости
лежит в плоскости
![]() тогда и только тогда, когда векторы
тогда и только тогда, когда векторы
![]() компланарны, и,
следовательно, когда их смешанное
произведение равно нулю
компланарны, и,
следовательно, когда их смешанное
произведение равно нулю
![]() .
.
Используя
это равенство, запишем уравнение
плоскости
![]() ,
заданной различными способами.
,
заданной различными способами.
|
Способы задания плоскости |
Данные и чертеж |
Условия для составления уравнения |
Уравнение |
|
Уравнение плоскости, заданной точкой и направляющим подпространством |
|
|
|
|
Уравнение плоскости, заданной тремя точками |
|
|
|
|
У |
Пусть отсекает соответствующие отрезки на осях координат:
на
на
оси
на
оси
|
|
|
|
Уравнение плоскости, заданной точкой и перпендикулярным вектором |
Определение
4.3.
Вектор
|
|
|
|
Параметрические уравнения плоскости |
|
|
|
Общее уравнение плоскости.
Пусть плоскость
задана точкой
![]() и
своим направляющим подпространством
(
и
своим направляющим подпространством
(![]() и
и
![]() ),
тогда в аффинной системе координат
плоскость
),
тогда в аффинной системе координат
плоскость
![]() задается
уравнением:
задается
уравнением:
 .
.
Раскрывая по элементам первого столбца определитель
![]() имеем уравнение
вида:
имеем уравнение
вида:
![]() .
.
Уравнение
вида
![]() называется общим уравнением прямой,
где
называется общим уравнением прямой,
где
![]() одновременно не равняются нулю (так как
векторы
одновременно не равняются нулю (так как
векторы
![]() и
и
![]() не являются коллинеарными) и
не являются коллинеарными) и
![]() .
.
Значит, общее уравнение прямой есть уравнение первой степени. Иными словами: любая плоскость есть поверхность первой степени.
Теорема 4.4.
Поверхность в пространстве, заданная
в аффинной системе координат уравнением
первой степени
![]() ,
есть плоскость. При этом векторы
,
есть плоскость. При этом векторы
![]() принадлежат
направляющему подпространству этой
плоскости и какие-либо два из них образуют
базис этого подпространства.
принадлежат
направляющему подпространству этой
плоскости и какие-либо два из них образуют
базис этого подпространства.
Доказательство.
-
По условию теоремы в уравнении
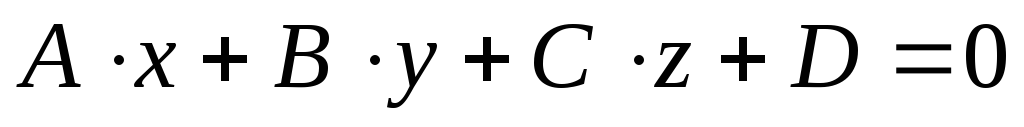 коэффициенты
коэффициенты
 одновременно не равны нулю. Пусть
одновременно не равны нулю. Пусть
 .
Помножив обе части равенства на
.
Помножив обе части равенства на
 и сгруппировав, имеем:
и сгруппировав, имеем:
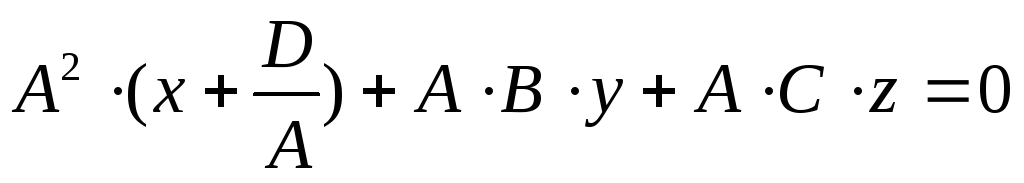 или
или
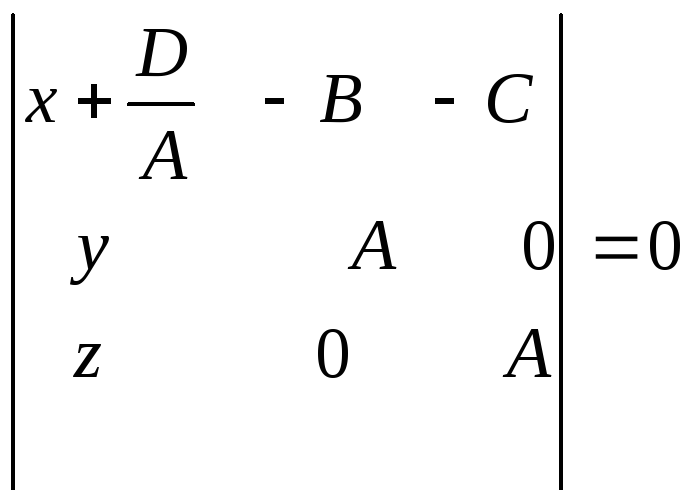 (1)
(1) -
Сравнивая уравнение (1) с уравнением плоскости, заданной точкой и направляющим подпространством, и учитывая, что
 ,
имеем: уравнение (1), а значит и ему
равносильное
,
имеем: уравнение (1), а значит и ему
равносильное
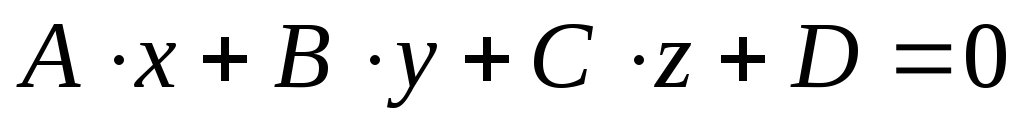 ,
определяет плоскость с направляющим
подпространством
,
определяет плоскость с направляющим
подпространством
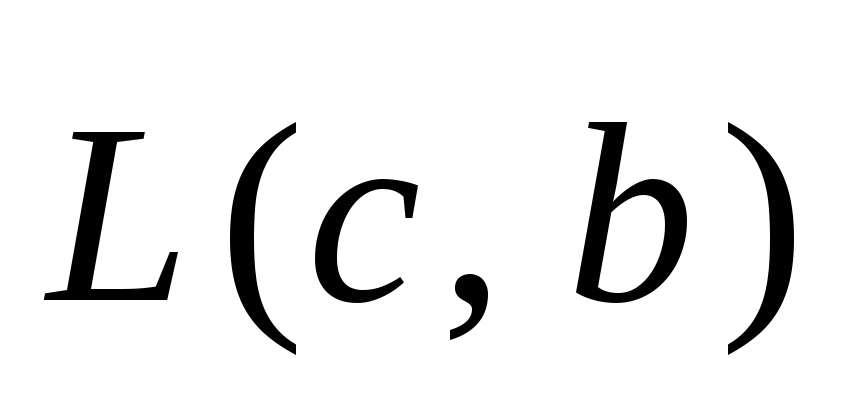 .
. -
Вектор
 принадлежит этому подпространству,
так как
принадлежит этому подпространству,
так как
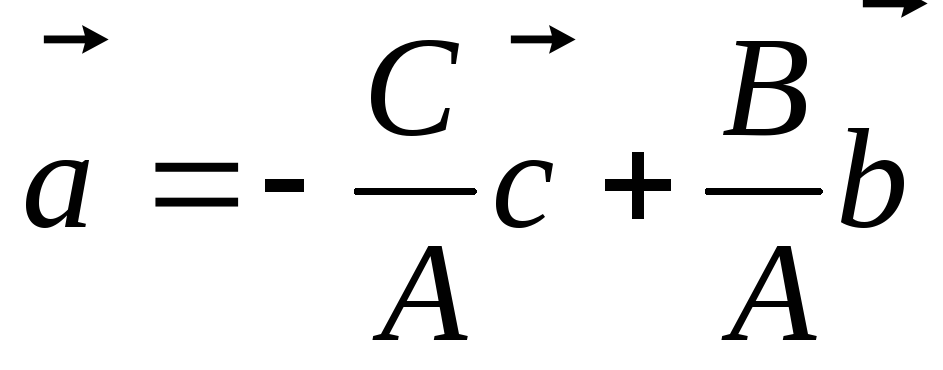 .
. -
Если в общем уравнении плоскости
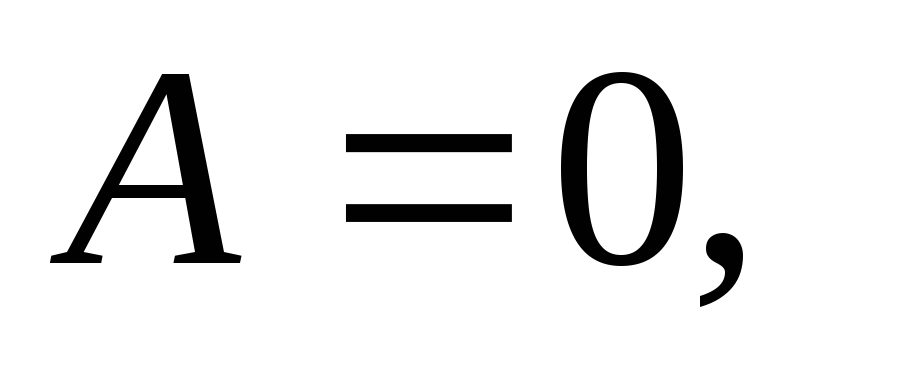 то
то
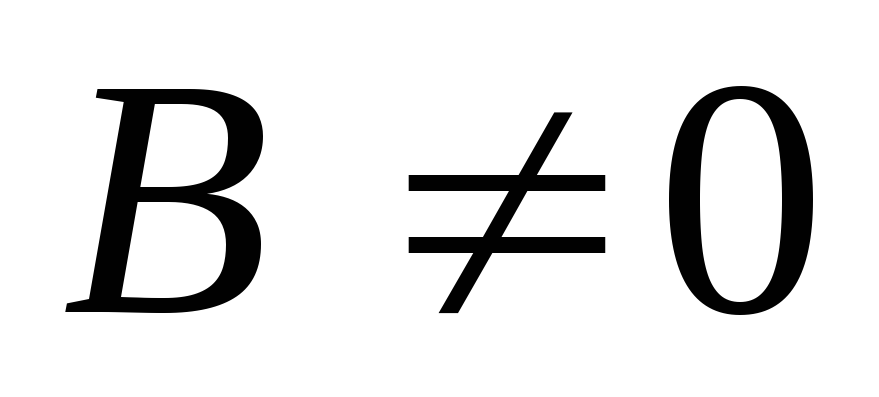 или
или
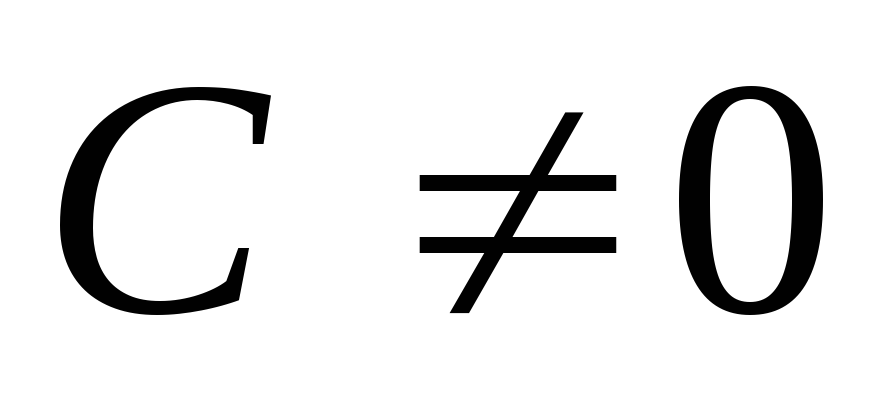 .
В каждом из этих случаев аналогичными
рассуждениями убеждаемся в том, что
уравнение
.
В каждом из этих случаев аналогичными
рассуждениями убеждаемся в том, что
уравнение
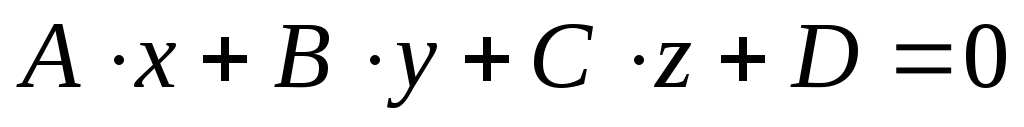 определяет плоскость, и векторы
определяет плоскость, и векторы
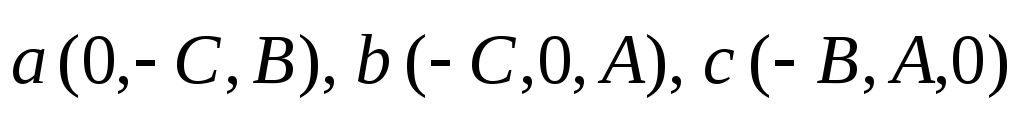 принадлежат
направляющему подпространству этой
плоскости
принадлежат
направляющему подпространству этой
плоскости
Геометрический смысл коэффициентов в общем уравнении плоскости.
Пусть плоскость
![]() задана
общим уравнением
задана
общим уравнением
![]() .
Выясним особенности в расположении
данной плоскости относительно системы
координат. Возможны следующие случаи:
.
Выясним особенности в расположении
данной плоскости относительно системы
координат. Возможны следующие случаи:
-
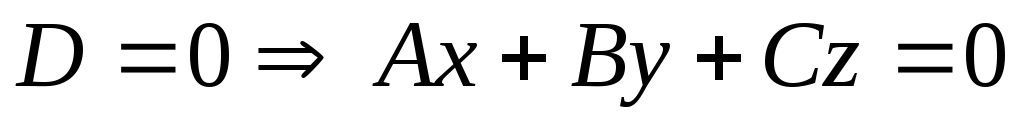 —плоскость
проходит через начало координат.
—плоскость
проходит через начало координат. -
 =>
=>
 .
Если
.
Если
 ,
то плоскость
,
то плоскость
 проходит через ось
проходит через ось
 .
. -
 =>
=>
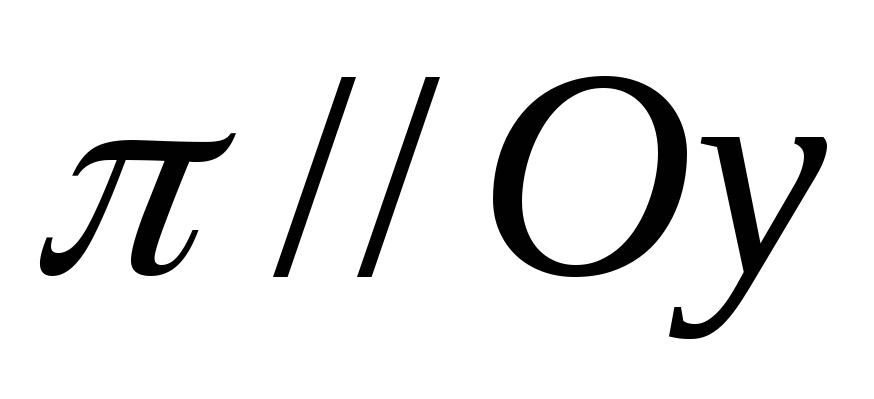 .
Если
.
Если
 ,
то плоскость
,
то плоскость
 проходит через
ось
проходит через
ось
 .
. -

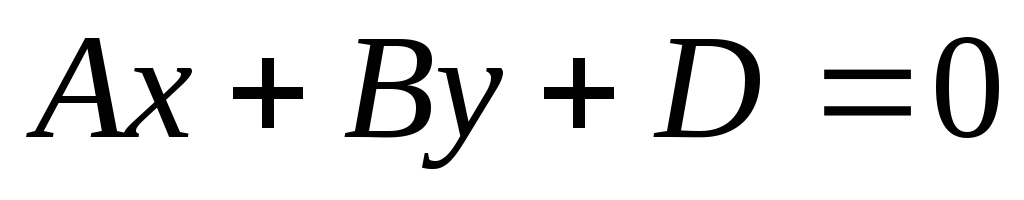
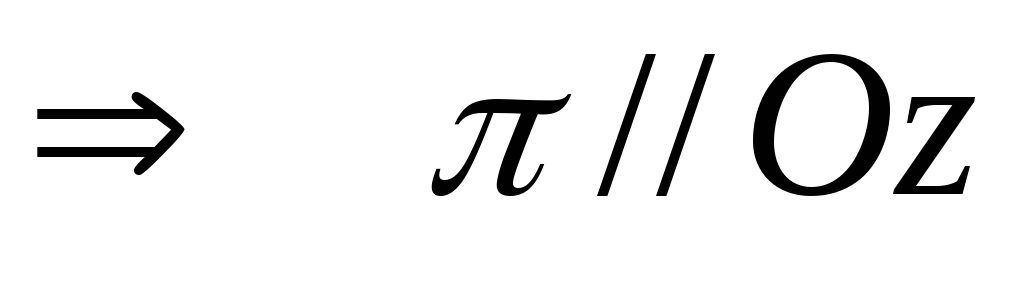 .
Если
.
Если
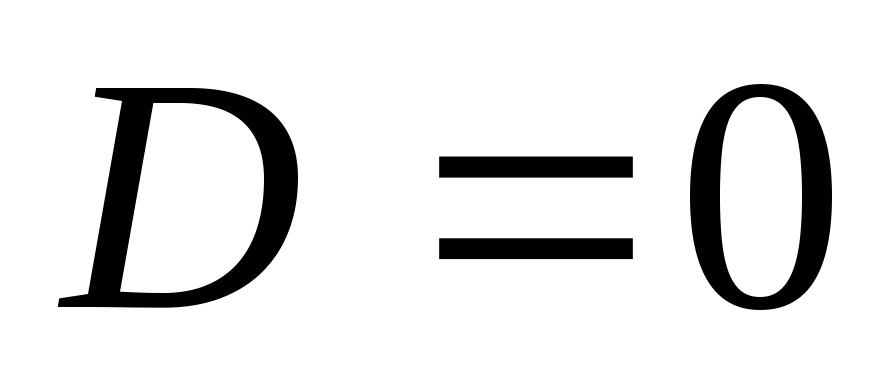 ,
то плоскость
,
то плоскость
 проходит через
ось
проходит через
ось
 .
. -
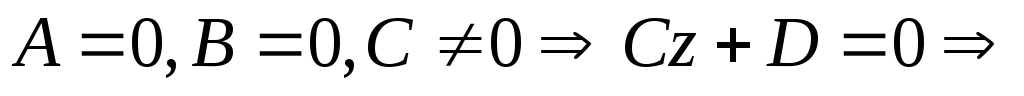
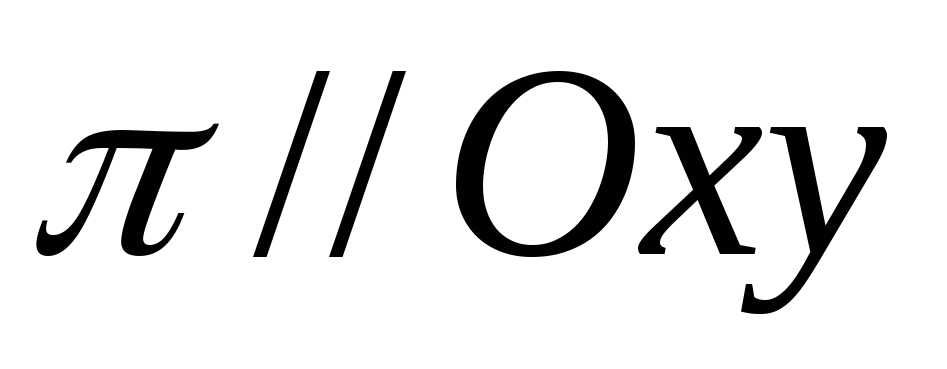 .
Если
.
Если
 ,
то плоскость
,
то плоскость
 совпадает с координатной плоскостью
совпадает с координатной плоскостью
 .
. -
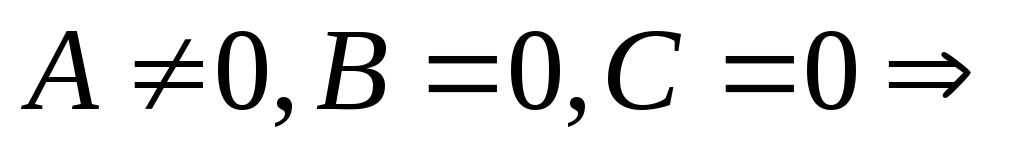
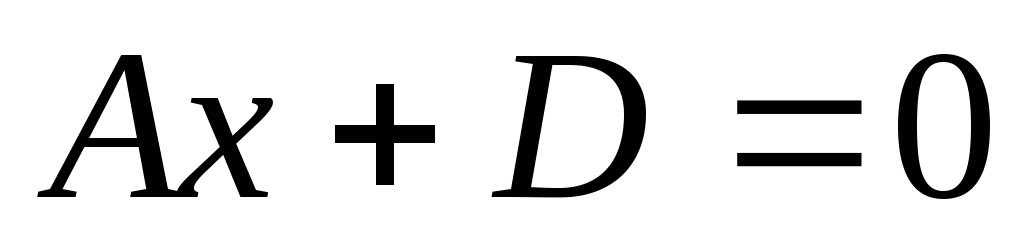
 .
Если
.
Если
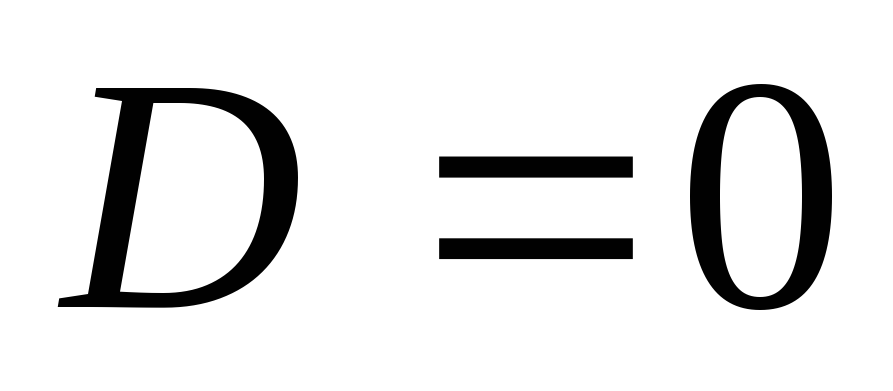 ,
то плоскость
,
то плоскость
 совпадает с координатной плоскостью
совпадает с координатной плоскостью
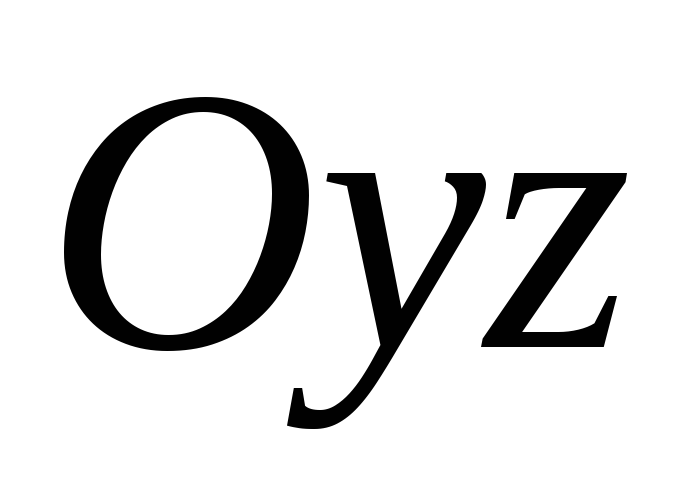 .
. -

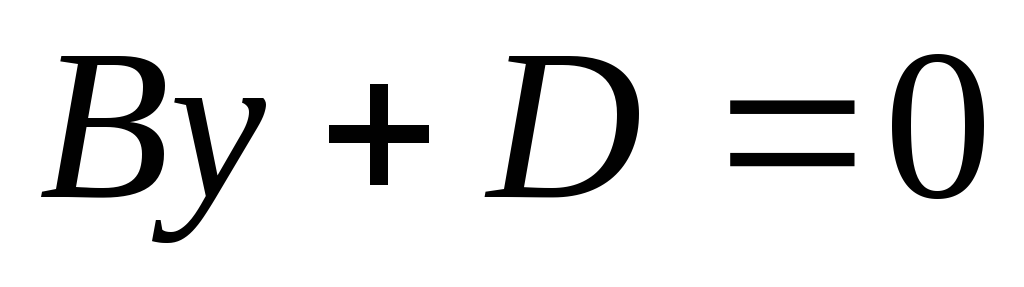
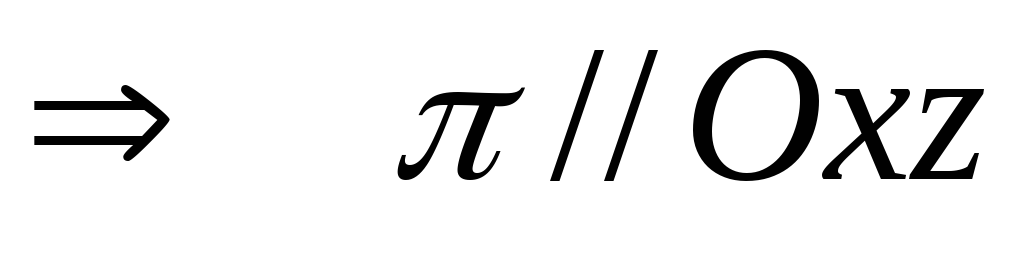 .
Если
.
Если
 ,
то плоскость
,
то плоскость
 совпадает с координатной плоскостью
совпадает с координатной плоскостью
 .
.
Геометрический
смысл знака многочлена
![]() .
.
Всякая плоскость разбивает пространство на два полупространства.
Точки
![]() и
и
![]() принадлежат одному полупространству,
если после подстановки их координат в
многочлен вида
принадлежат одному полупространству,
если после подстановки их координат в
многочлен вида
![]() ,
получаем значение одного знака, иначе
точки
,
получаем значение одного знака, иначе
точки
![]() и
и
![]() принадлежат разным
полупространствам.
принадлежат разным
полупространствам.
Р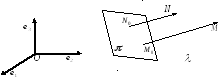 ассмотрим
в аффинной системе координат
ассмотрим
в аффинной системе координат
![]() плоскость
,
заданную общим уравнением. Вектор
плоскость
,
заданную общим уравнением. Вектор
![]() перпендикулярен
к плоскости .
Точка
перпендикулярен
к плоскости .
Точка
![]() не принадлежит плоскости .
не принадлежит плоскости .
1. Зафиксируем на
плоскости
![]() некоторую точку
некоторую точку
![]() и отложим от нее вектор
и отложим от нее вектор
![]() ,
т.е.
,
т.е.
![]() .
.
2.
Проведем через произвольную точку
![]() пространства
прямую, параллельную
вектору
пространства
прямую, параллельную
вектору
![]() и пересекающую плоскость
в точке
и пересекающую плоскость
в точке
![]() .
.
3. Так как векторы
![]() и
и
![]() коллинеарны, то
коллинеарны, то
![]() ,
где R.
Иначе в координатах, имеем:
,
где R.
Иначе в координатах, имеем:
![]() .
.
4.
Рассмотрим многочлен
![]() и подставим вместо
и подставим вместо
![]() их значения:
их значения:
![]() (*)
(*)
5. Пусть
![]() - полупространство с границей
- полупространство с границей
![]() ,
содержащее точку
,
содержащее точку
![]() .
Из равенства
.
Из равенства
![]() следует, что точка
следует, что точка
![]() принадлежит полупространству
принадлежит полупространству
![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() .
Из равенства (*), учитывая, что
.
Из равенства (*), учитывая, что
![]() приходим к выводу, что точка
приходим к выводу, что точка
![]() принадлежит полупространству
принадлежит полупространству
![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() .
Это и есть неравенство, определяющее
полупространство
.
Это и есть неравенство, определяющее
полупространство
![]() .
Неравенство
.
Неравенство
![]() определяет другое полупространство
определяет другое полупространство
![]() с границей
с границей
![]() .
.
Задача:
Даны
точки
![]() ,
,
![]() ,
,
![]() и плоскость
и плоскость
![]() .
Среди указанных точек выбрать те, каждая
из которых с началом координат лежит
по разные стороны от данной плоскости.
.
Среди указанных точек выбрать те, каждая
из которых с началом координат лежит
по разные стороны от данной плоскости.

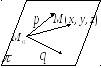

 -произвольная
точка плоскости
-произвольная
точка плоскости
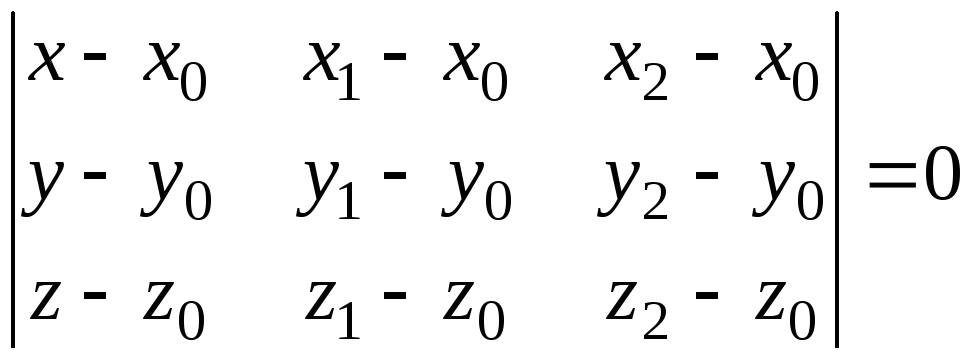
 равнение
плоскости в отрезках
равнение
плоскости в отрезках