
Лаб 3 Решен. прям. и обрат. зад. магниторазведки
.docМинистерство общего и профессионального
Образования Российской федерации
Томский политехнический университет
Методические указания к лабораторной работе
«Решение прямой и обратной задач магниторазведки»
по курсу «Геологическая интерпретация геофизических данных»
Томск 2015
Решение прямой и обратной задач магниторазведки.
Цель и состав работы
Целью настоящей работы является знакомство с методикой решения прямой и обратной задач магниторазведки.
Задачей работы является:
-
определение характера распределения магнитного поля от тела изометричной формы (прямая задача);
-
определение формы, размеров и положения тела изометричной формы по данным имеющегося аномального поля (обратная задача).
По итогам выполненных работ составляется отчет о методике решения поставленных задач и о результатах их решений.
Общие сведения по интерпретации геофизических данных
Геологическую интерпретацию геофизических данных проводят с целью дать обоснованное решение геологических задач, поставленных проектом работ, и извлечь из имеющихся материалов наиболее полную информацию об особенностях геологического строения изучаемого участка земной поверхности.
При интерпретации очень важно установить природу отдельных геофизических аномалий или аномальных зон и попытаться выяснить, какие геологические процессы привели к образованию тел, обладающих аномальными свойствами ( намагничением, силой тяжести, электрическим сопротивлением и др.) по отношению к окружающим породам.
Интерпретация полученных материалов выполняется в несколько этапов.
Вначале выполняют качественную интерпретацию, которая заключается в следующем:
1. на основании изученных свойств пород (магнитных, электромагнитных и др.) устанавливают наиболее вероятные геологические факторы, обуславливающие характер физического поля в данном районе;
2. по морфологии наблюдаемого поля (наличие однотипных областей-с нормальными, спокойными, пониженными или повышенными значениями, характеристика отдельных аномалий - интенсивность, форма, размеры, простирание и т.п. ) определяют плановое положение тех или иных структурных элементов, происхождение и состав пород их слагающих;
3. выделяются участки требующие постановки детализационных работ или исследований другими геофизическими методами;
4. обосновываются возможности количественной интерпретации.
Вторым этапом интерпретации является количественное истолкование полученных материалов, при котором путем математических расчетов определяется глубина залегания, форма, размеры и свойства геологических объектов, вызывающих данную аномалию.
В количественной интерпретации выделяют прямую и обратную задачи.
Прямая задача заключается в определении характера распределения физического поля (магнитного, электромагнитного, гравитационного и др.), создаваемого телом (телами) заданной формы, объема и свойства.
Обратная задача заключается в определении формы, размеров и положения тела (тел) по данным измеренного аномального поля. Обратная задача обычно имеет неоднозначное решение, т.е. тела разных объемов, размеров, положений и свойств могут иметь одинаковое аномальное поле.
Исходными материалами для интерпретации данных магниторазведки являются графики и карты изолиний составляющих магнитного поля (вертикальной Z, горизонтальной Н) или полного вектора Т, сведения о магнитных свойствах горных пород (магнитной восприимчивости , интенсивности намагничения J , остаточной намагниченности и др.).
Для того, чтобы производить интерпретацию аномалий тем или иным методом, т.е. решать обратную задачу тем или иным методом, необходимо прежде всего уметь решать этими методами прямые задачи, т.е. уметь вычислять аномалии от заданных форм тел. При этом обратный ход решения прямой задачи будет давать путь и прием для интерпретации.
Важность решения прямых задач состоит еще в том, что в результате этих расчетов заранее определяются и изучаются возможные величины и формы аномалий от различных объектов. Руководствуясь этим, во многих случаях сразу можно давать более правильные объяснения получаемым результатам съемки.
При расчете и интерпретации магнитных аномалий почти всегда принимаются следующие условности и допущения:
-
Допускается однородность намагничения возмущающих тел.
-
Допускается сплошность и монолитность тел, т.е. они считаются сплошными, без пустот, без разрывов и пр.
-
Часто, например при аналитических приемах интерпретации, по форме аномалии приходится заранее ориентировочно предопределять или даже условно задаваться наиболее подходящей геометрически правильной формой возмущающего тела.
-
Иногда приходиться принимать для расчетов ориентировочные значения интенсивности намагничения тел, если они не известны, и заранее определять или условно задаваться направлением намагниченности тел.
Прямая задача магниторазведки решается:
- аналитическим способом - для тел простой формы (шар, цилиндр, шток, пласт);
- графически – с помощью специальных номограмм и палеток для тел изометричной формы.
Обратная задача решается способами:
- характерных точек,
- касательных,
- подбора,
- сравнения.
Решение прямой задачи магниторазведки в данной лабораторной работе рассмотрим на примере вычисления магнитного поля горизонтального бесконечного цилиндра произвольного сечения, намагниченного вертикально.
Решение задачи осуществляется с помощью цилиндрической палетки Д.С. Микова.
Палетка позволяет вычислять элементы вектора аномального поля Zа и На от двумерных тел при однородной вертикальной и наклонной намагниченности.
Палетка представляет собой вертикальное сечение нижнего полупространства в предположении, что оно заполнено веществом с магнитной восприимчивостью однородно намагниченным полем Z оп , направленным по оси палетки Jz . Сечение разбито на отдельные площадки равного действия, представляющие собой сечение элементарных цилиндров.
Форма, положение и размер каждого цилиндра выбраны так, чтобы аномалия от каждого цилиндра в центре палетки была равна 1гамме (1нТл).
Площадки для удобства счета заменены точками, поставленными в центры влияния площадок.
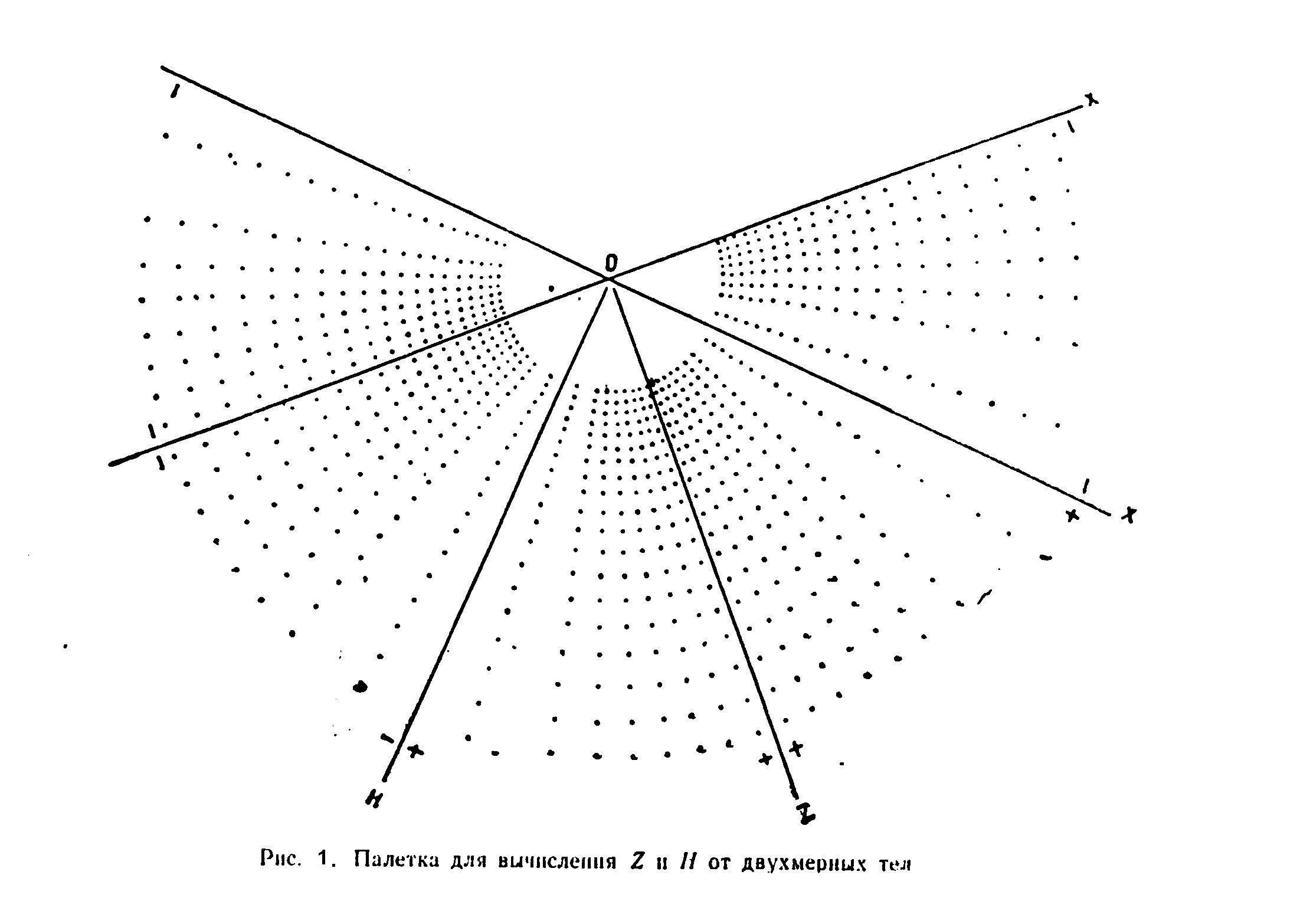
Расчет Zа при вертикальном намагничении выполняется в следующем порядке.
Дается:
- вертикальное сечение тела по профилю вкрест его простирания,
- рельеф дневной поверхности,
- масштаб разреза,
- значение J
На разрезе намечают и нумеруют расчетные точки профиля. Они должны располагаться на поверхности наблюдений – предполагаемых или проведенных, в связи с этим их намечают с учетом высоты штатива и масштаба разреза.
При вычислении Zа центр палетки совмещают с точкой 1 профиля, палетку ориентируют так, чтобы ось Jz была направлена по Zо, т.е. вертикально вниз. Подсчитывают точки, попавшие в контур поперечного сечения тела с учетом их знака, и находят их алгебраическую сумму S1. Вычисляют переходный коэффициент, представляющий собой отношение намагниченностей, принятых для разреза (J) и палетки (Jп) и равный
К = J/Jп
Поле в точке 1 определяется произведением
Zа1 = K*S1*1γ(нТл)
Так же находится поле для всех точек профиля поочередно.
При расчете На изменяют ориентировку палетки, а именно, по Zо направляют другую ось палетки – ось Jн.
Эта же палетка может быть использована для расчета Zа и На от двумерных тел при наклонной намагниченности их. В этом случае вместо Zо д.б. дано намагничивающее поле Rо , действующее в плоскости профиля и представляющее собой проекцию вектора То на эту плоскость. Прямую задачу решают в том же порядке, но переходный коэффициент вычисляют по формуле
К = Rо*χ *10/100
и изменяют ориентировку палетки, а именно, соответствующую ось палетки направляют по биссектрисе угла косого намагничения I – угла отклонения Rо от вертикали.
Вторая часть лабораторной работы – решение обратной задачи заключается в определении параметров аномального тела аппроксимированного вертикально намагниченным круговым горизонтальным цилиндром, поле которого представлено на рисунке 2.
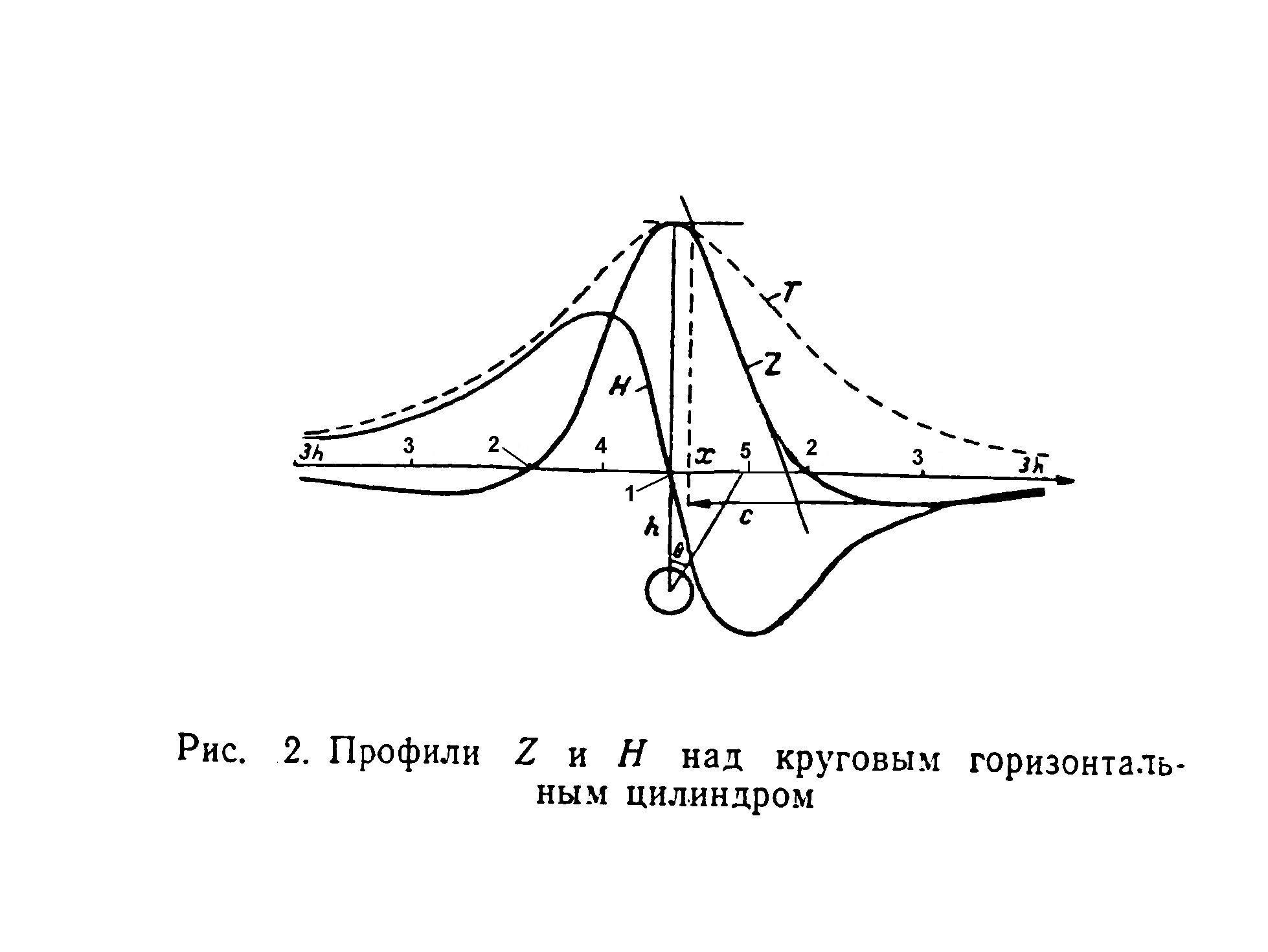
Значения Z и Н определяются формулами:
Z = 2М*(h²-x²)/(h²+x²)²,
Н = -2М*2hx/(h²+x²)²,
Где М - магнитный момент единицы длины цилиндра, равный произведению вертикальной интенсивности намагничения J на площадь поперечного сечения цилиндра S, т.е.
М = J*S = J*π*R².
Анализ кривых этих уравнений показывает, что:
-
над центром тела (x1 = 0) Н = 0, а Z имеет максимальное значение, равное
Zm = 2М/h²;
2. при x2 = +h , Z=0;
3. при x3 = +1.73h Z имеет наибольшие отрицательные значения равные 0,125Zm;
4. при x4 = -0.41h кривые Z и Н пересекаются и каждая имеет значение 0,61Zm;
5. при x5 = +0,57h H имеет максимальные значения равные 0,65Zm;
6. В плане аномалия будет вытянута по всему простиранию рудного тела, а векторы Н будут направлены в сторону магнитного тела.
При решении обратной задачи можно определить глубину залегания оси цилиндра:
- по кривой Zа- как половину расстояния между точками перехода кривой через нуль;
- по кривой Н – по формуле h = xэ√3, где xэ- половина расстояния между экстремумами кривой.
Таким образом, глубина центра залежи при интерпретации определяется соотношениями:
h = x1 = x 2/1.73 = x3 / 0.57 = x4 / 0.41
Зная h можно вычислить магнитный момент единицы длины М, например по Zаm
М = 0,5Zаm*h²
При известном из других источников J можно определить площадь поперечного сечения
S = M/J,
радиус сечения цилиндра
R = √ S/π или R = √ М/J π,
глубину до верхней кромки тела (минимальную глубину скважины)
H1 = h-R.
Литература
-
Гринкевич Г. И. Магниторазведка. Изд-во «Недра», 1971.
-
Логачев А. А., Захаров В.П. Магниторазведка. Изд-во «Недра», 1973.
-
Миков Д.С. Методы интерпритации магнитных аномалий. Изд-во Томского университета, 1975.
-
Магниторазведка. Справочник геофизика./Под редакцией В.Е. Никитского, Ю.С. Глебовского. - М. : Недра, 1980.
-
Палетки Д.С. Микова….?
Магнитные свойства пород
