3 курс 1 семестр (задания) / Теория автоматического управления (Булавин В.Ф

7

Контрольная работа № 1

Типовые звенья систем автоматического регулирования

Цель работы: изучение типовых звеньев систем автоматического регулирования и построение частотных, временных и логарифмических характеристик.

Теоретическая часть

Звенья систем автоматического управления и регулирования различаются по виду их передаточной функции (или дифференциального уравнения), определяющей все их динамические свойства и характеристики. Основными типами звеньев являются: позиционные, дифференцирующие и интегрирующие.

Позиционными звеньями называются такие, передаточные функции которых имеют вид:

, ,

где - изображение по Лапласу сигнала на входе звена; - изображение по Лапласу сигнала на выходе звена; -коэффициент усиления звена; s -оператор Лапласа; многочлены и имеют свободные члены, равные 1, то есть эти звенья обладают статической характеристикой (при ), определяющей их состояние равновесия (свойство позиционности).

У дифференцирующих звеньев передаточная функция имеет вид

,

где имеет свободный член, равный 1. Для двукратно дифференцирующего звена числитель передаточной функции имеет вид .

Передаточные функции интегрирующих звеньев имеют соответственно вид:

или ,

где имеет свободный член, равный 1.

Основными позиционными звеньями являются:

- идеальное усилительное звено

, ;

- апериодическое звено первого порядка

, ,

где - оператор дифференцирования;

- апериодическое звено второго порядка

, , при ;

- колебательное звено

, ,

где - коэффициент демпфирования, .

К интегрирующим звеньям относятся:

- идеальное интегрирующее звено

или , ;

- инерциальное интегрирующее звено

, .

К дифференцирующим звеньям относятся:

- идеальное дифференцирующее звено

, ;

- форсирующее звено

, .

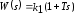Основные характеристики звеньев

Амплитудно-фазовая частотная характеристика (АФЧХ) звена определяется

путем подстановки в операторную передаточную функцию звена (где - круговая частота, ) и выделении действительной и мнимой частей.

Например, для апериодического звена 1-го порядка получаем

Амплитудная частотная характеристика звена (АЧХ): .

Фазовая частотная характеристика звена (ФЧХ): .

В терминах MathCad указанные операции легко могут быть проведены следующим образом:

Логарифмическая амплитудно-фазовая частотная характеристика (ЛАФЧХ):

.

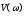
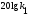
-45

-90

Рис.1. АФЧХ и ЛАФЧХ для апериодического звена 1-го порядка

Переходная и весовая функции звена

Переходной функцией называется реакция звена на единичное ступенчатое воздействие, то есть переходный процесс на выходе 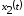при единичном скачке на входе звена.

Следовательно,

, ,

откуда переходная функция

.

Используя переходную характеристику, можно определить реакцию на входное воздействие , заданное произвольной кривой при помощи интеграла Дюамеля

.

1

0 0

а) б)

Рис.2. График единичной ступенчатой функции (а) и

реакция типового колебательного звена (б)

Часто встречающимся воздействием на реальные системы являются кратковременные, но существенные по величине всплески, импульсы. Например, порывы ветра, ударная нагрузка и т. п. Моделирование подобного рода воздействий осуществляется с помощью единичной импульсной функции , имеющей следующее определение

при .

Импульсная единичная функция относится к классу обобщенных функций и представляет собой производную от единичной ступенчатой функции:

.

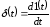Реакцию звена или системы на единичную импульсную функцию называют импульсной характеристикой (весовой функцией). Между весовой и переходной функциями звена или системы имеется следующее соотношение:

.

Пример аналитического выражения переходной и весовой функций для колебательного звена:

, .

При колебания становятся незатухающими, а при колебания превращаются в апериодический процесс.

Перед выполнением лабораторной работы создать в папке своей группы MathCad-документ, в котором будут оформлены все проводимые работы.

Порядок выполнения работы

1. По таблицам 1 и 2 выбрать исходные данные в соответствии с вариантом задания, состоящим из 2-х цифр.

Таблица 1

Параметр	Значение
Вариант	1	2	3	4	5	6	7	8	9	10	11	12	13
k1	30	40	50	60	70	80	90	100	110	120	35	45	55
T1	0,1	0,2	0,3	0,4	0,5	0,6	0,05	0,06	0,07	0,08	0,07	0,35	0,45
T2	0,01	0,02	0,1	0,15	0,06	0,2	0,01	0,01	0,02	0,02	0,015	0,12	0,15
	0,4	0,5	0,6	0,5	0,3	0,4	0,7	0,8	0,5	0,3	0,25	0,25	0,25

Таблица 2

Вариант	1	2	3	4	5	6	7	8	9	10	11	12	13
Звено	K	A1	A2	K	A1	A2	K	A1	A2	K	A1	A2	K

где K- колебательное звено;

A₁ - апериодическое звено 1-го порядка;

A₂ - апериодическое звено 2-го порядка.

2. Сформулировать цель работы и записать исходные данные: дифференциальное уравнение, параметры и передаточную функцию звена.

3. Получить формулы для построения основных характеристик звена.

4. С помощью программы MathCad построить графики основных характеристик.

5. По результатам построения определить время переходного процесса.

6. Исследовать, как изменяется переходная характеристика звена при уменьшении (увеличении) одного из параметров звена.

Контрольные вопросы

1. Что такое передаточная функция звена?

2. Какие основные характеристики звена существуют?

3. Что такое весовая функция?

4. Что такое переходная функция звена?

Переходной функцией называется реакция звена на единичное ступенчатое воздействие, то есть переходный процесс на выходе при единичном скачке на входе звена.

5. Как построить АФЧХ звена?

6. Приведите простейшие преобразования, используемые для упрощения структурных схем САУ.

7. Дайте определение обратной связи (положительной и отрицательной).

8. Приведите математические выражения прямого и обратного преобразований Лапласа.

систем”)