
- •Глава 1. Прямая на плоскости
- •§ 1 Вступление
- •§ 2 Задачи, при решении которых используется уравнение прямой .
- •Список формул
- •Пример 4. Луч света направлен по прямой . Дойдя до прямой, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.
- •Пример 5. Из точки направлен луч света под углом 45 к прямой . Дойдя до этой прямой, луч от нее отразился. Составить уравнения падающего и отраженного лучей.
- •Вычислить тангенс угла между прямыми ,.Ответ:
- •§ 4 Взаимное расположение прямых на плоскости .
- •§ 5 Примеры решения задач и задачи для самостоятельного решения
- •Известны уравнения двух сторон ромба ,и уравнение одной из его диагоналей. Составить уравнение второй диагонали.Ответ: .
- •§ 3 Взаимное расположение плоскостей.
- •Глава 3. Прямая в пространстве
- •§ 1 Вступление
- •§ 2 Вывод уравнения пространственной прямой при разных способах ее задания.
- •§ 3 Взаимное расположение пространственных прямых.
- •Глава 4. Прямая и плоскость в пространстве
- •§ 1 Вступление
- •§ 2 Взаимное расположение прямой и плоскости в пространстве.
- •§3 Задачи для самостоятельного решения
- •Глава 1. Прямая на плоскости 3
§ 5 Примеры решения задач и задачи для самостоятельного решения
Основные методы составления уравнений прямых наглядно можно продемонстрировать на примере построения уравнений линейных элементов треугольника .
Пример15.
Треугольник
![]() задан координатами своих вершин:
задан координатами своих вершин:![]() ,
,![]() и
и![]() (Рис. 9)
(Рис. 9)
Найти:
м
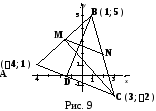 едиану
едиану ;
;среднюю линию
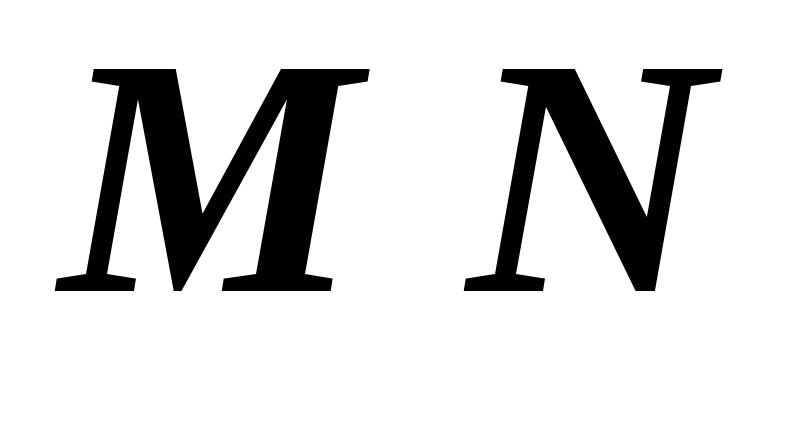 ;
;высоту
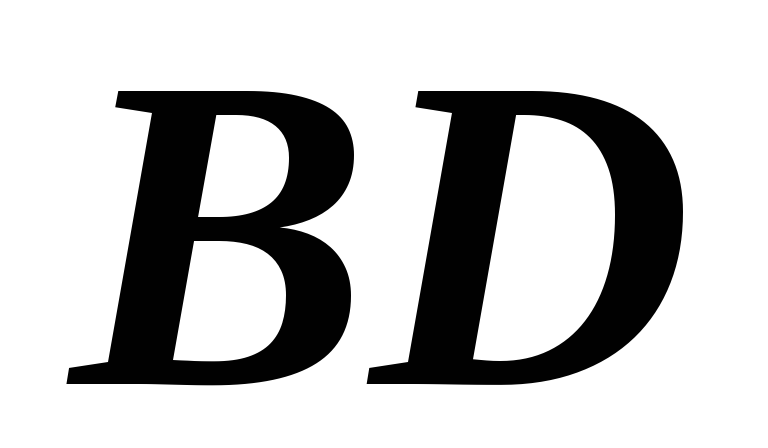 ;
;биссектрису
 ;
;центр описанной окружности.
Решение.
Найдем медиану
 .
Вычислим координаты точки
.
Вычислим координаты точки
середины отрезка
середины отрезка
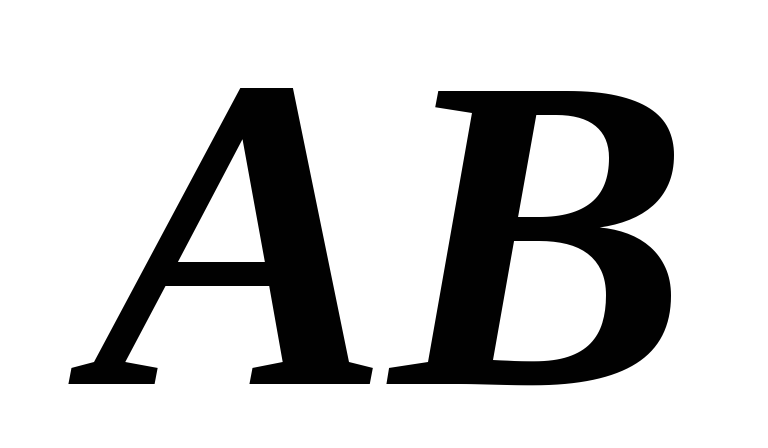 .
.
![]() .
Уравнение
.
Уравнение![]() найдем
по двум точкам:
найдем
по двум точкам:
![]() .
.
Найдем среднюю линию
 .
.
Способ
1. Вычислим
координаты середины стороны
![]()
точки
точки
![]() .
.![]() .
Уравнение
.
Уравнение![]() найдем по двум точкам:
найдем по двум точкам:
![]()
![]() .
.
Способ
2. Найдем
![]() по
точке
по
точке![]() и направляющему вектору, в качестве
которого можно взять вектор
и направляющему вектору, в качестве
которого можно взять вектор![]() .
.
Вычислим:
![]() .
.
Тогда:
![]()
![]()
Очевидно,
что для
![]() получилось то же уравнение, что и при
первом способе.
получилось то же уравнение, что и при
первом способе.
Уравнение высоты
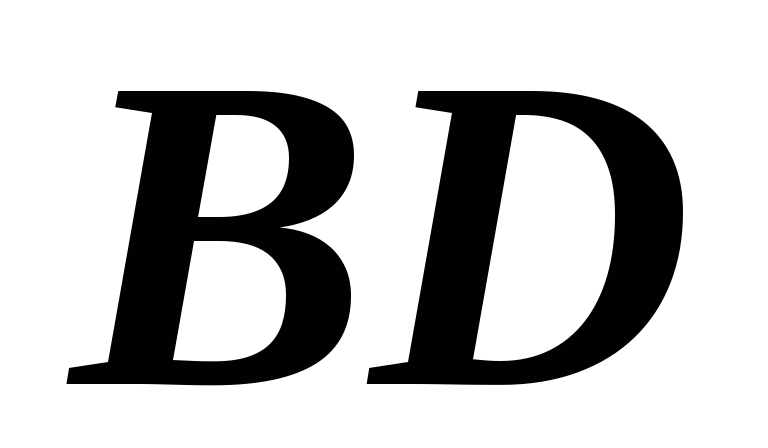 найдем по точке и перпендикулярному
вектору, в качестве которого можно
взять вектор
найдем по точке и перпендикулярному
вектору, в качестве которого можно
взять вектор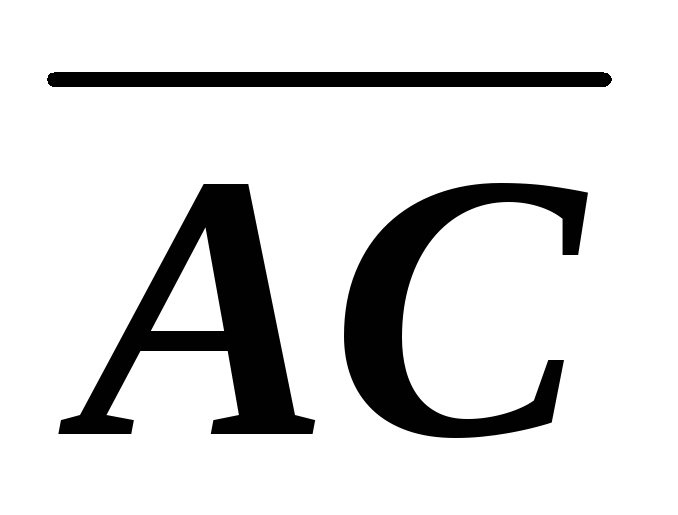 .
.
![]() .
.
Биссектрису
 можно найти разными способами (Рис.
10). Но, если числовые данные в задаче
специально не подобраны, то все эти
способы приводят к громоздким
вычислениям. Наиболее легким для
запоминания является способ, основанный
на следующем факте:
можно найти разными способами (Рис.
10). Но, если числовые данные в задаче
специально не подобраны, то все эти
способы приводят к громоздким
вычислениям. Наиболее легким для
запоминания является способ, основанный
на следующем факте:
в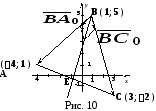 ектор
суммы векторов одинаковой длины идет
в точности по биссектрисе угла,
образованного этими векторами (свойство
ромба).
ектор
суммы векторов одинаковой длины идет
в точности по биссектрисе угла,
образованного этими векторами (свойство
ромба).
Поскольку
требуется найти биссектрису угла
![]() ,
то возьмем два вектора, исходящих именно
из этой вершины:
,
то возьмем два вектора, исходящих именно
из этой вершины:![]() и
и![]() .
Вычислим их длины:
.
Вычислим их длины:
![]() ;
;
![]() .
.
Очевидно,
что их длины не равны. А теперь от
векторов
![]() и
и![]() перейдем к их ортам
перейдем к их ортам![]() и
и![]() ,
векторам с тем же направлением, но
одинаковой единичной длины.
,
векторам с тем же направлением, но
одинаковой единичной длины.
![]() ;
;
![]() .
.
Построим новый вектор
![]()
![]() .
.
Этот вектор уже можно использовать в качестве направляющего для биссектрисы, но работать с ним нелегко. Вместо него можно взять другой вектор, попроще.
![]()
Корни, конечно, никуда не исчезли, но, по крайней мере, не стало дробей.
По
формуле (9) имеем:
![]()
Если
Вам не нравится отрицательный коэффициент
при
![]() ,
умножьте все уравнение на (1
):
,
умножьте все уравнение на (1
):
Найдем центр окружности, описанной вокруг треугольника
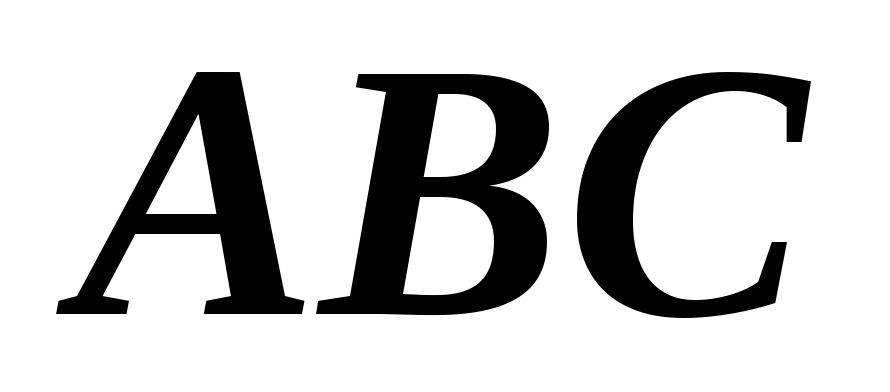 .
.
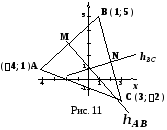
Он,
как известно, находится в точке
пересечения любых двух серединных
перпендикуляров треугольника
![]() (Рис.11)..
(Рис.11)..
Поскольку ранее
были найдены координаты середин сторон
![]() и
и![]() ,
найдем уравнения серединных перпендикуляров
именно к этим сторонам:
,
найдем уравнения серединных перпендикуляров
именно к этим сторонам:![]() и
и![]() .
.
Для
![]() имеем:
имеем:
|
точка
|
|
Для
![]() имеем:
имеем:
|
точка
|
|
Найдем точку пересечения полученных серединных перпендикуляров:
![]() и
и
![]()
![]()
Воспользуемся формулами Крамера:
![]() ;
;
![]() ;
;
![]() .
.
![]() ;
;
![]()
Задачи для самостоятельного решения
Известны уравнения двух сторон ромба ,и уравнение одной из его диагоналей. Составить уравнение второй диагонали.Ответ: .
Известны уравнения двух сторон ромба
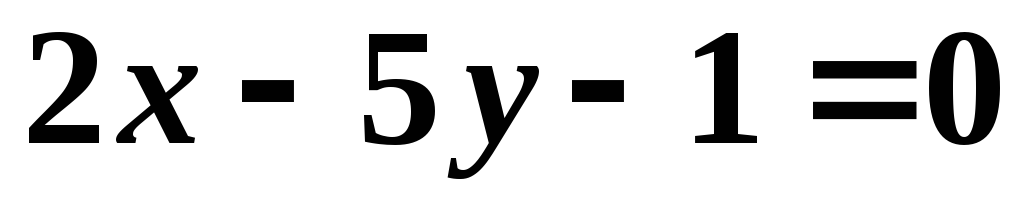 ,
,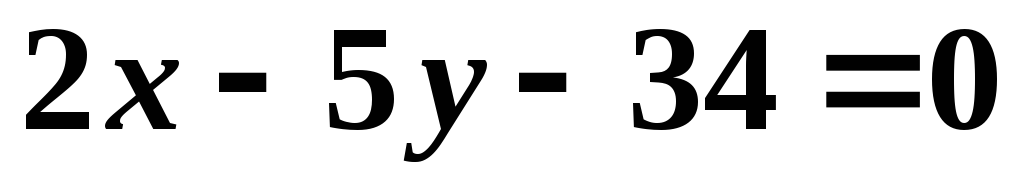 и уравнение одной из его диагоналей
и уравнение одной из его диагоналей .
Составить уравнение второй
диагонали.Ответ:
.
Составить уравнение второй
диагонали.Ответ: 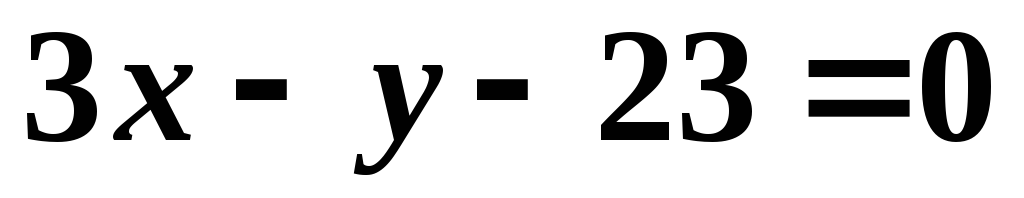 .
.Даны уравнения двух сторон параллелограмма
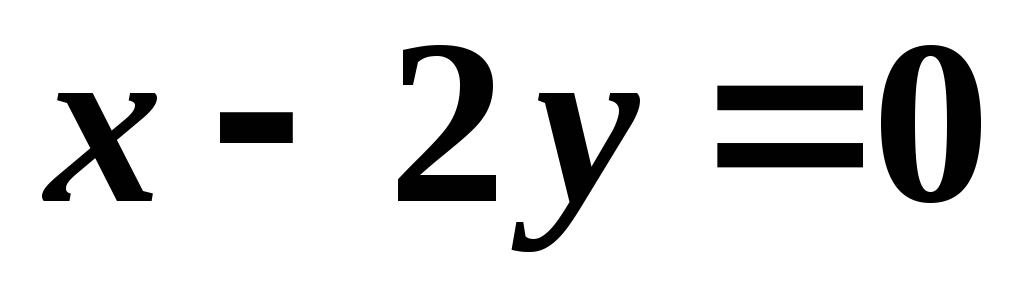 ,
,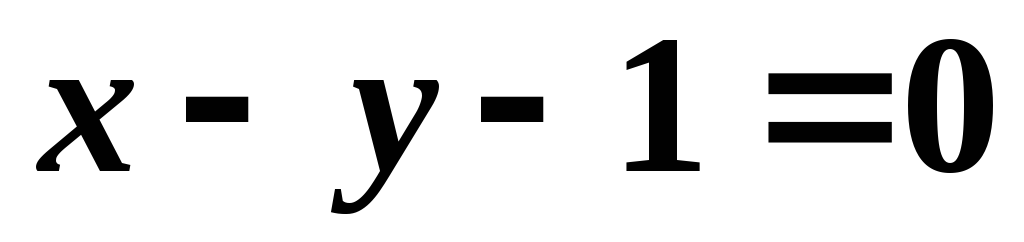 и точка пересечения его диагоналей
и точка пересечения его диагоналей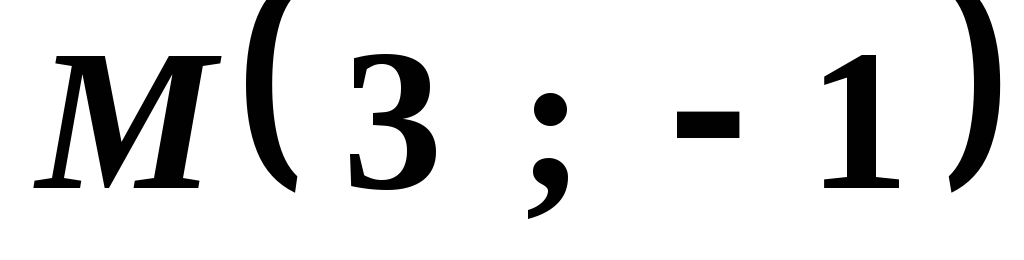 .
Найти уравнения двух других сторон.
Ответ:
.
Найти уравнения двух других сторон.
Ответ: 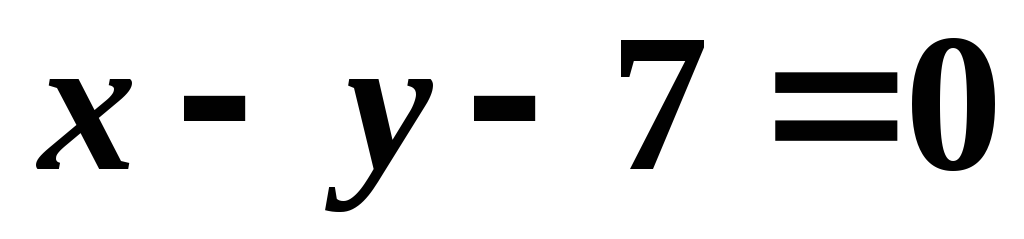 ,
,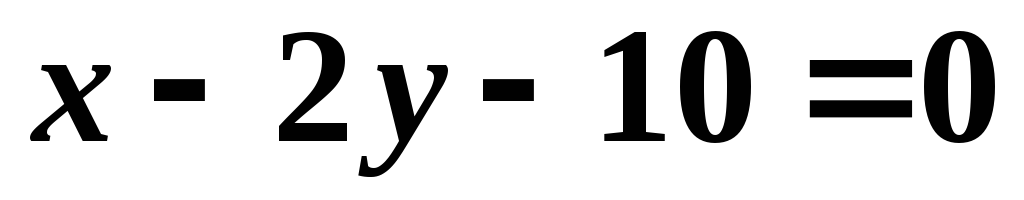 .
.Даны вершины треугольника
 ,
,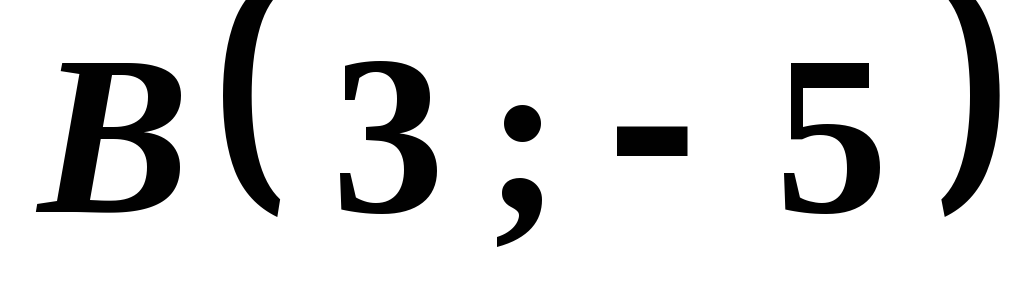 и
и .
Составить уравнение перпендикуляра,
опущенного из вершины
.
Составить уравнение перпендикуляра,
опущенного из вершины на
биссектрису внутреннего угла при
вершине
на
биссектрису внутреннего угла при
вершине .Ответ:
.Ответ:  .
.Найти точку
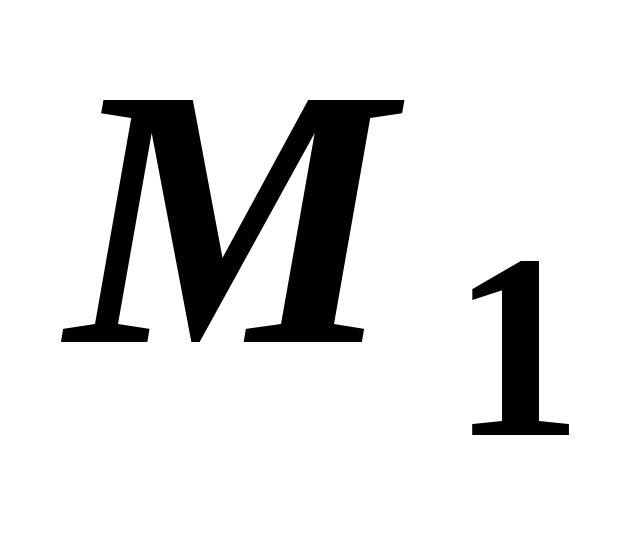 ,
симметричную точке
,
симметричную точке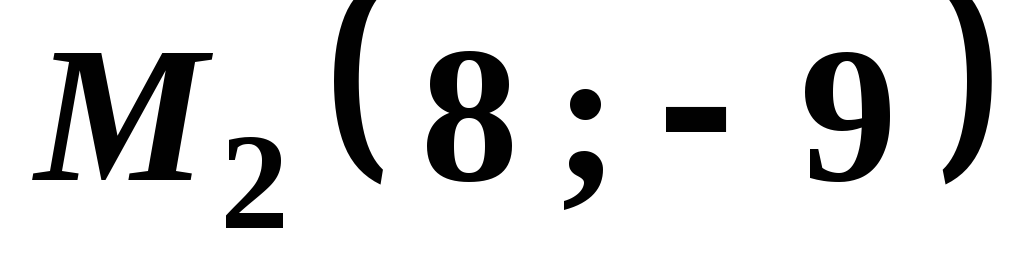 относительно прямой, проходящей
через точки
относительно прямой, проходящей
через точки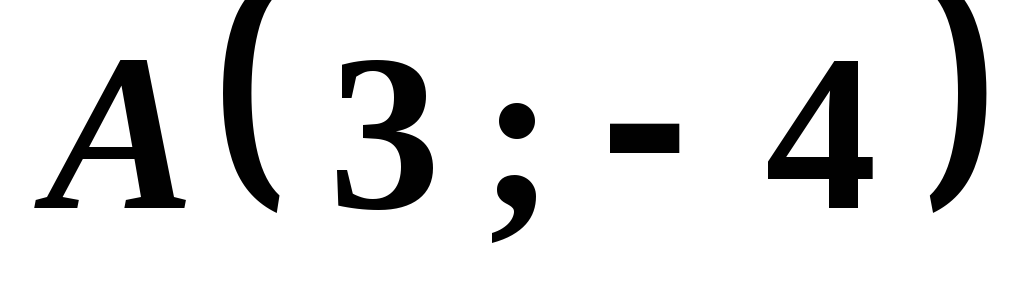 и
и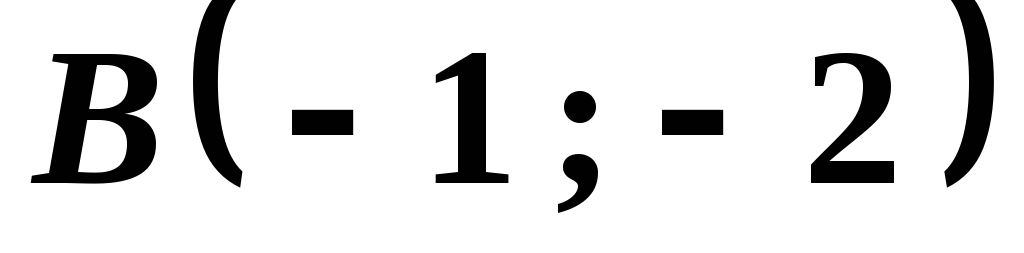 .
.
Ответ:![]() .
.
Точки
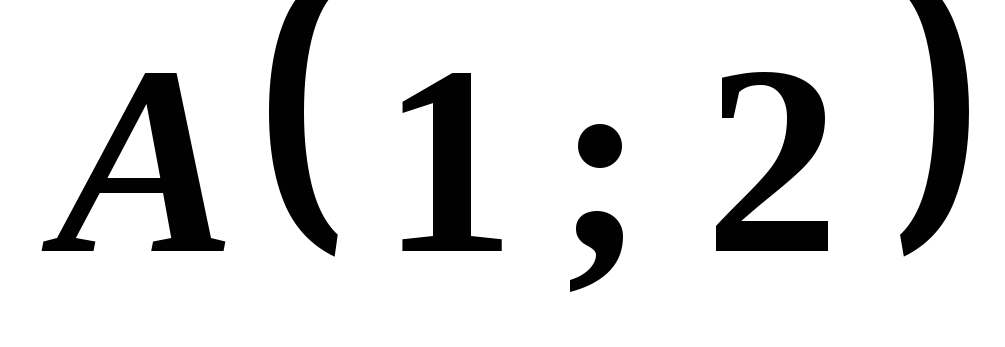 и
и являются
противоположными вершинами квадрата.
Определить координаты двух других
вершин квадрата.
являются
противоположными вершинами квадрата.
Определить координаты двух других
вершин квадрата.
Ответ:![]() и
и![]()
Найти прямые, принадлежащие пучку
 и
перпендикулярные основным прямым
пучка.
и
перпендикулярные основным прямым
пучка.
Ответ: ![]() ,
,![]() .
.
Даны стороны треугольника:
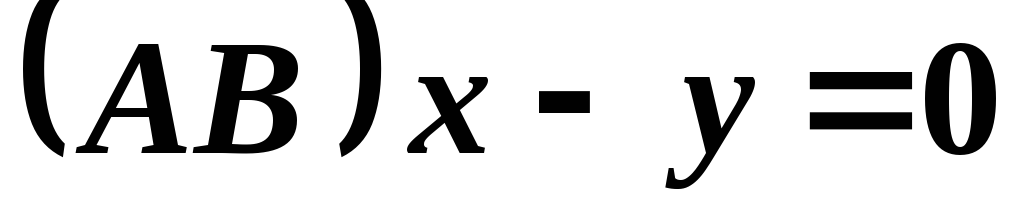 ;
;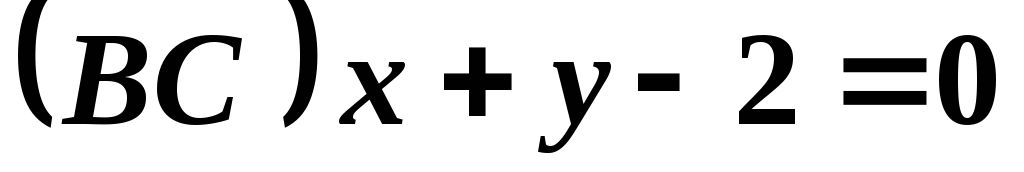 и
и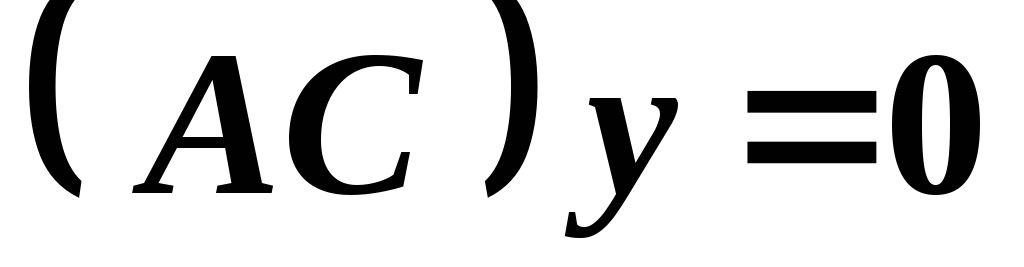 .
Составить уравнения медианы ,
проходящей через вершину
.
Составить уравнения медианы ,
проходящей через вершину ,
и высоты, проходящей через вершину
,
и высоты, проходящей через вершину .Ответ:
.Ответ:
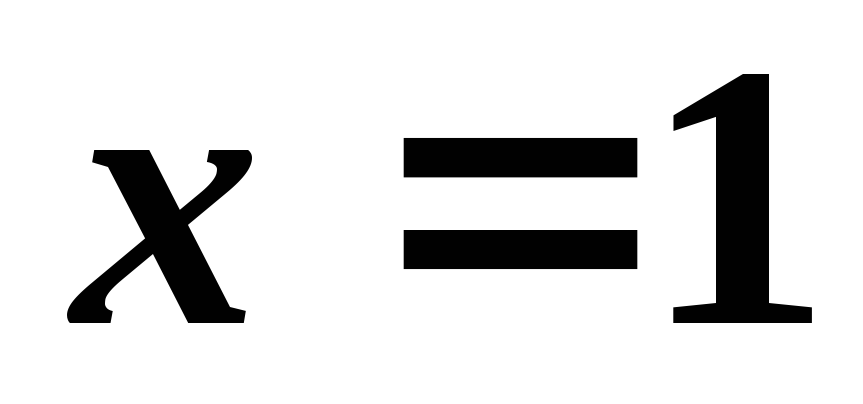 ,
,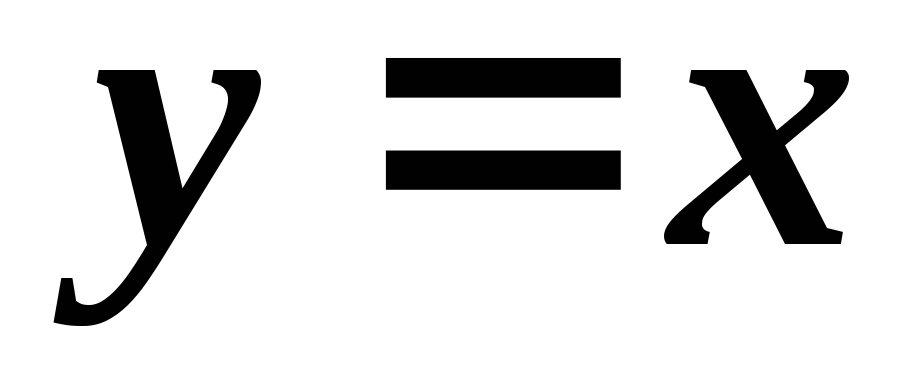 .
.Составить уравнения трех сторон квадрата, если известно, что четвертой стороной являются отрезок прямой
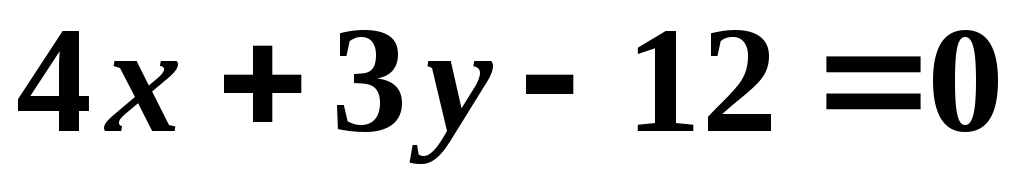 ,
концы которого лежат на осях координат.
,
концы которого лежат на осях координат.
Ответ: ![]() ,
,![]() ,
,![]() или
или![]() .
.
Доказать, что четырехугольник с вершинами
 ,
,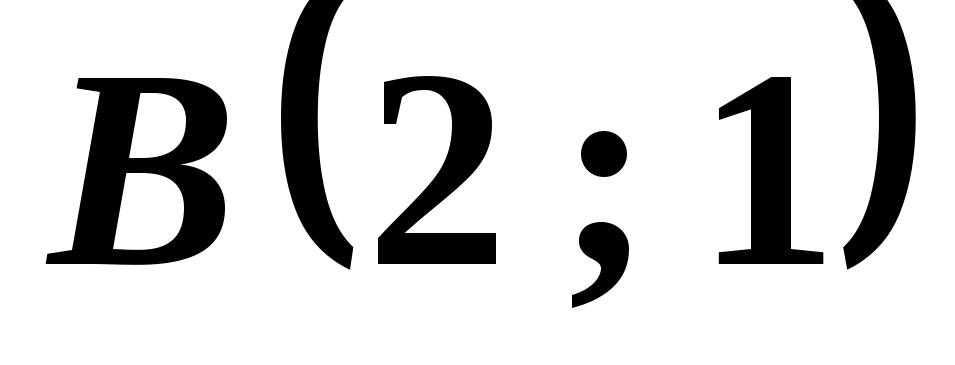 ,
, и
и –
трапеция. Найти точку пересечения
средней линии трапеции и высоты,
опущенной из вершины С на сторону
–
трапеция. Найти точку пересечения
средней линии трапеции и высоты,
опущенной из вершины С на сторону
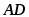 .
.
Ответ:![]()
Вершины четырехугольника:
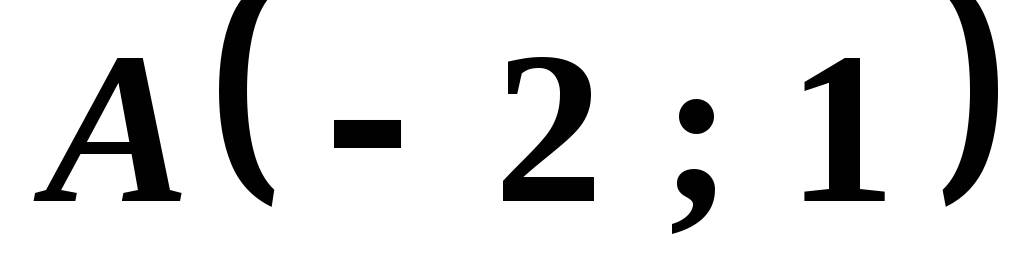 ,
,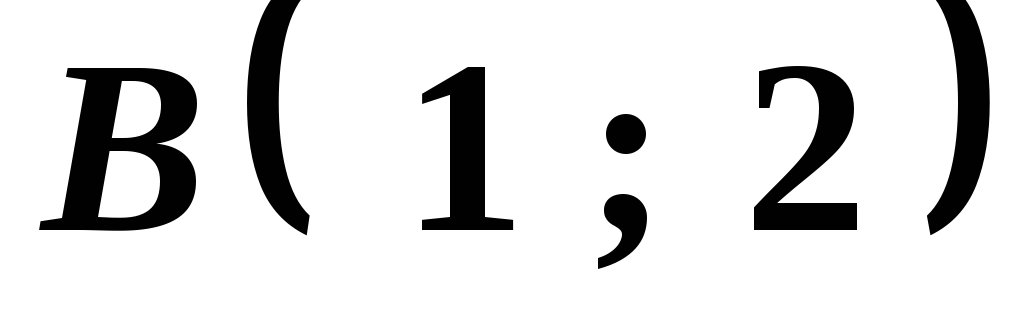 ,
, ,
,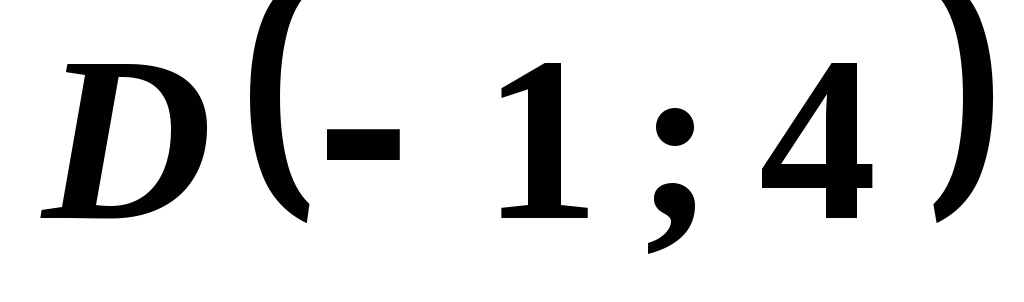 .
Доказать, что этот четырехугольник
ромб. Найти точку пересечения
перпендикуляра из вершины
.
Доказать, что этот четырехугольник
ромб. Найти точку пересечения
перпендикуляра из вершины
 на
сторону
на
сторону с прямой, проходящей через вершину
и середину
с прямой, проходящей через вершину
и середину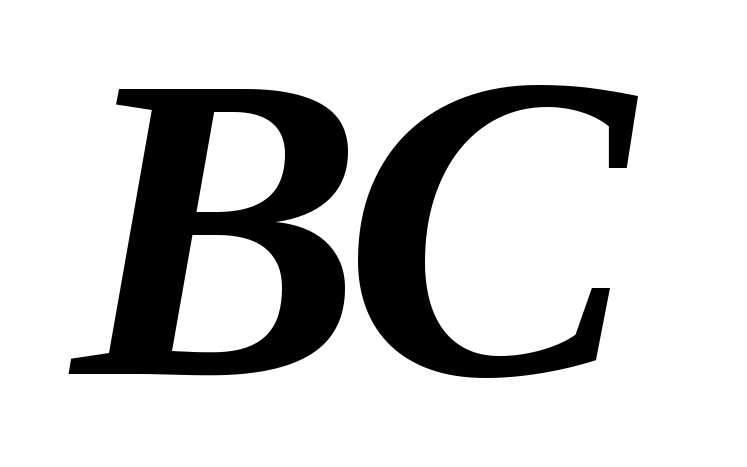 .
.
Ответ:![]()
Даны три из четырёх вершин трапеции
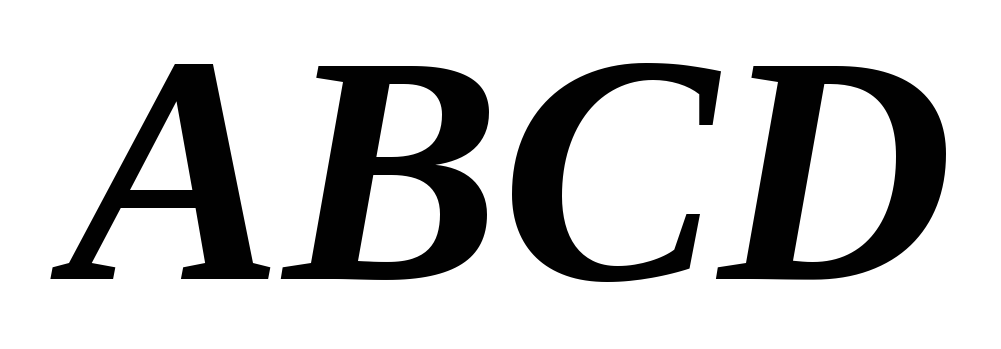 :
: .
Известно, что диагонали трапеции
взаимно перпендикулярны. Найти
координаты вершины
.
Известно, что диагонали трапеции
взаимно перпендикулярны. Найти
координаты вершины этой трапеции.
этой трапеции.
Ответ:![]()
ГЛАВА 2. Плоскость
§ 1 Вступление
В
аналитической геометрии плоскость
![]() это геометрическое множество точек в
пространстве, координаты которых
удовлетворяют уравнению
это геометрическое множество точек в
пространстве, координаты которых
удовлетворяют уравнению
![]() .
.
![]() общее уравнение
плоскости;
общее уравнение
плоскости;
![]() уравнение
плоскости в отрезках,
уравнение
плоскости в отрезках,
где
![]() абсцисса точки пересечения плоскости
абсцисса точки пересечения плоскости![]() с
осью
с
осью![]() ;
;![]() ордината точки пересечения
ордината точки пересечения![]() с
осью
с
осью![]() ,
а
,
а![]() аппликата точки
пересечения
аппликата точки
пересечения![]() с
осью
с
осью![]() .
.
§ 2 Вывод уравнения плоскости при разных способах ее задания.
Уравнение плоскости, проходящей через три заданных точки
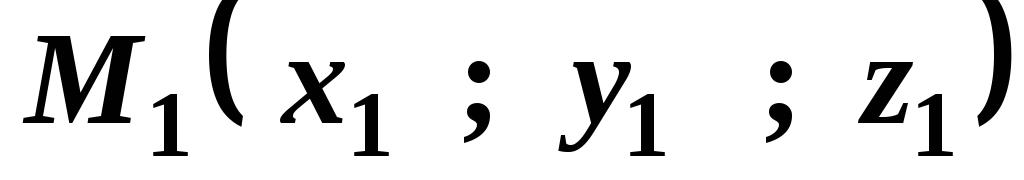 ,
,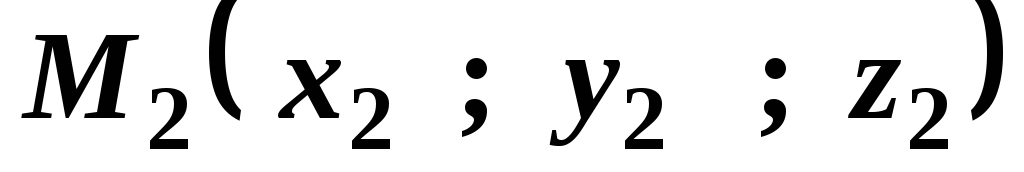 и
и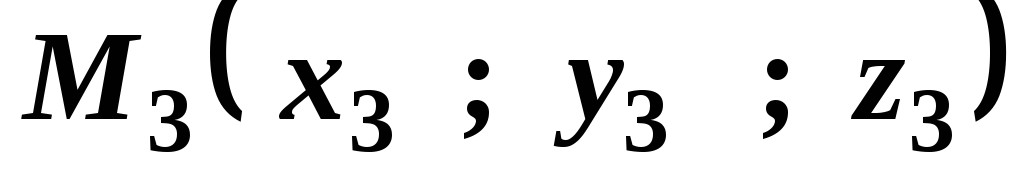 ,
не лежащие на одной прямой.
,
не лежащие на одной прямой.
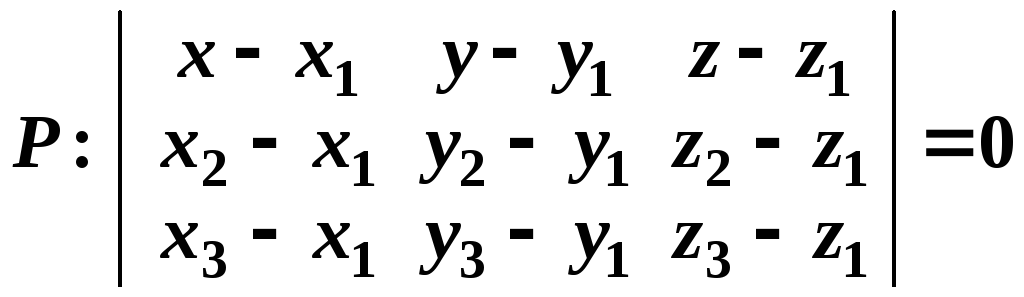 (15)
(15)
Чтобы
получить общее уравнение плоскости
![]() ,
нужно символьно вычислить этот
определитель, например, разложив его
по первой строке.
,
нужно символьно вычислить этот
определитель, например, разложив его
по первой строке.
Пример16.
Даны вершины тетраэдра:
![]() ,
,![]() ,
,![]() и
и![]() .
Найти уравнение грани
.
Найти уравнение грани![]() .
.
Р
D(-1;0;5) С(2;2;0) А(3;-1;1) В(-4;1;0) ешение.Замечу, что эту задачу можно решать
«вслепую», без чертежа. Но для лучшего
понимания методов решения, чертеж (хотя
бы схематический) лучше все-таки
нарисовать.
ешение.Замечу, что эту задачу можно решать
«вслепую», без чертежа. Но для лучшего
понимания методов решения, чертеж (хотя
бы схематический) лучше все-таки
нарисовать.
Обозначим![]() произвольная точка
плоскости, в которой лежит основание
произвольная точка
плоскости, в которой лежит основание![]() .
.
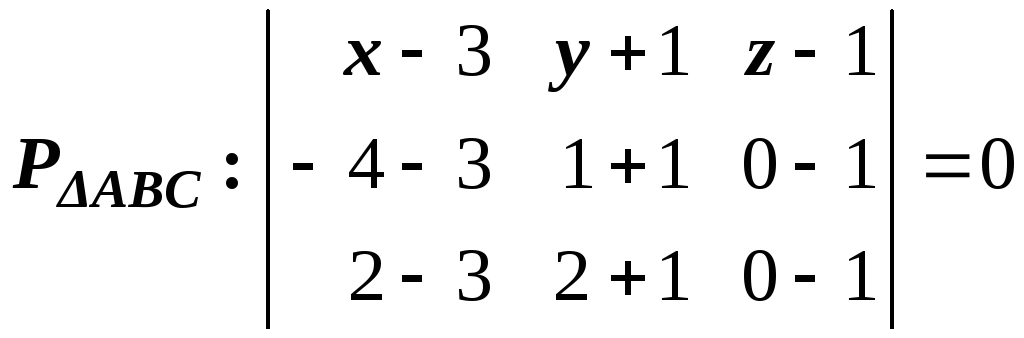
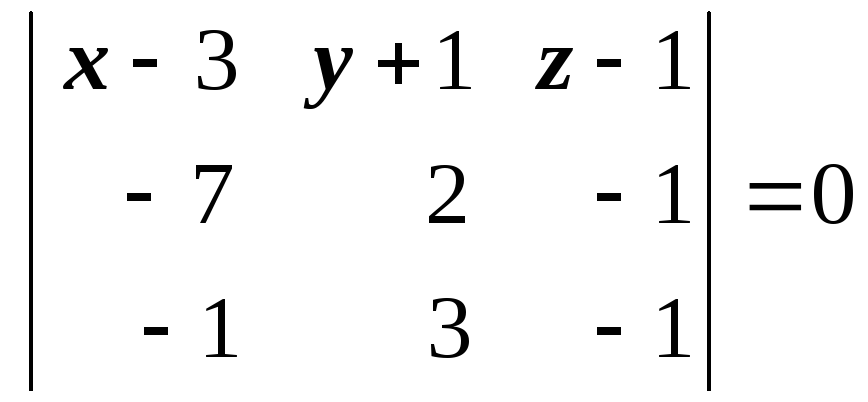
![]()
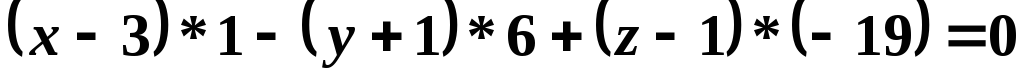 .
.
Окончательно
![]() .
.
Уравнение плоскости, проходящей через данную точку
 перпендикулярно данному вектору
перпендикулярно данному вектору
![]() (16)
(16)
Пример17.Даны вершины тетраэдра:![]() ,
,![]() ,
,![]() и
и![]() .
Найти уравнение плоскости, проходящей
через вершину
.
Найти уравнение плоскости, проходящей
через вершину![]() перпендикулярно ребру
перпендикулярно ребру![]() .
.
Решение.Искомая плоскость![]() изображена на Рис 13. Так как по условию
плоскость
изображена на Рис 13. Так как по условию
плоскость![]() перпендикулярна боковому ребру
перпендикулярна боковому ребру![]() ,
то вектор
,
то вектор![]() перпендикулярен плоскости треугольника
перпендикулярен плоскости треугольника![]() .
Точка
.
Точка![]() .
.
Тогда
![]()
![]() .
.
Пример
18.
Известно, что точки:
![]() и
и![]() симметричны относительно некоторой
плоскости
симметричны относительно некоторой
плоскости![]() .
Найти уравнение этой плоскости.
.
Найти уравнение этой плоскости.
Р
B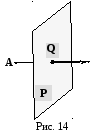 ешение.
Искомая плоскость изображена на Рис.14.
Поскольку по условию точки
ешение.
Искомая плоскость изображена на Рис.14.
Поскольку по условию точки
![]() и
и![]() симметричны
относительно плоскости
симметричны
относительно плоскости![]() ,
то они лежат на перпендикуляре к этой
плоскости, проходящем через
,
то они лежат на перпендикуляре к этой
плоскости, проходящем через![]() и
и![]() .
Так как
.
Так как![]() и
и![]() равноудалены
от плоскости
равноудалены
от плоскости![]() ,
то эта плоскость проходит через середину
отрезка
,
то эта плоскость проходит через середину
отрезка![]()
точку
точку
![]() .
Нарисуем вектор
.
Нарисуем вектор![]() и введем его аналитически
и введем его аналитически![]() .
Вычислим координаты точки
.
Вычислим координаты точки![]() :
:![]() . По формуле (16 ) построим
уравнение искомой плоскости
. По формуле (16 ) построим
уравнение искомой плоскости
![]()
![]() /
поделим на (
4) /
/
поделим на (
4) /
![]() .
.
Уравнение плоскости, проходящей через данную точку
 параллельно двум непараллельным
векторам
параллельно двум непараллельным
векторам
 и
и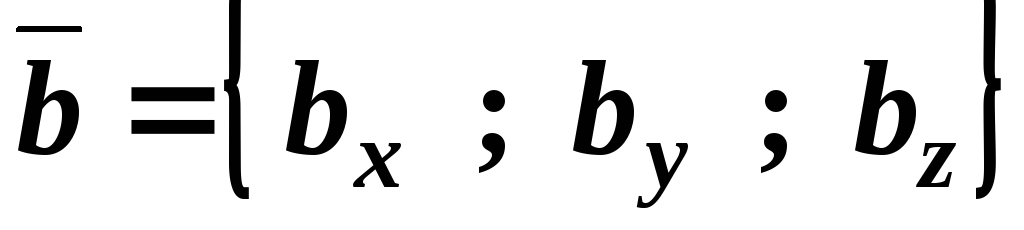 .
.
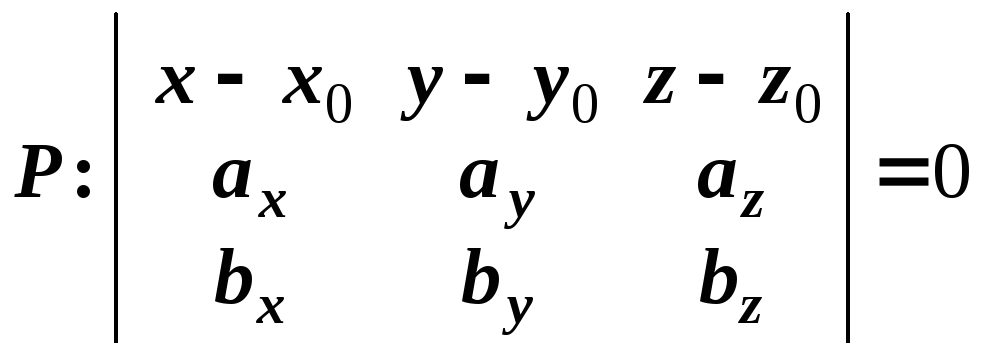 (17)
(17)
Замечание. Решение многих задач на составление уравнения плоскости на практике сводится к поиску трех компланарных векторов. Их смешанное произведение, как известно, равно нулю. В координатах смешанное произведение вычисляется с помощью определителя 3-го порядка, строки которого и есть координаты этих трех векторов. Именно в этом и заключается смысл формул (15) и (17 ).
П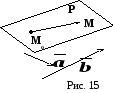 ример
19.
Составить уравнение плоскости, проходящей
через точку
ример
19.
Составить уравнение плоскости, проходящей
через точку
![]() параллельно двум векторам
параллельно двум векторам![]() и
и![]() .
.
Решение.
Прежде всего заметим, что векторы
![]() и
и![]() не параллельны, так как их координаты
не пропорциональны
не параллельны, так как их координаты
не пропорциональны![]() (Рис.15). Далее, обозначим
(Рис.15). Далее, обозначим![]()
произвольная точка искомой плоскости.
Нарисуем вектор
произвольная точка искомой плоскости.
Нарисуем вектор
![]() и введем его аналитически
и введем его аналитически![]() .
По условию искомая плоскость параллельна
векторам
.
По условию искомая плоскость параллельна
векторам![]() и
и![]() или, что то же самое, векторы
или, что то же самое, векторы![]() и
и![]() параллельны искомой плоскости . Это в
свою очередь означает, что параллельным
переносом векторы
параллельны искомой плоскости . Это в
свою очередь означает, что параллельным
переносом векторы![]() и
и![]() можно переместить в плоскость вектора
можно переместить в плоскость вектора![]() .
Следовательно все три вектора
.
Следовательно все три вектора![]() ,
,![]() и
и![]() компланарны и их смешанное произведение
компланарны и их смешанное произведение![]() ,
что в координатах дает уравнение
,
что в координатах дает уравнение
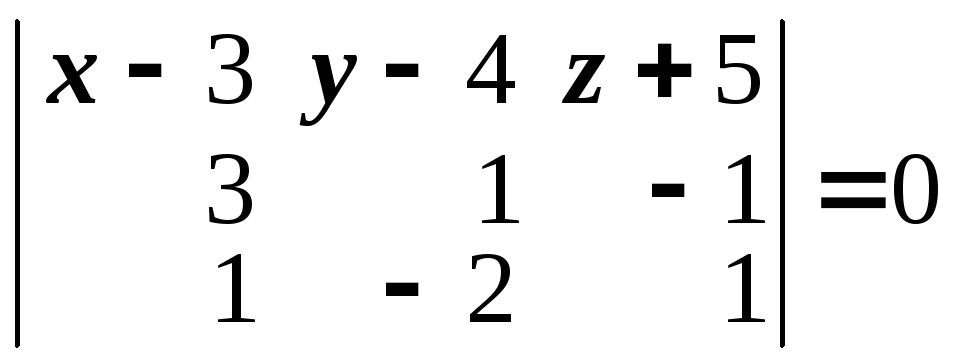
![]()
![]() или
или
![]() .
.
Уравнение плоскости, проходящей через две заданных точки
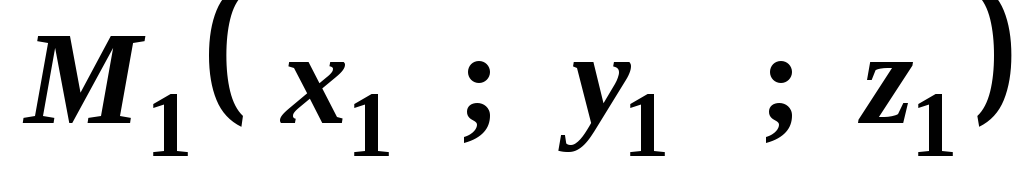 ,
, параллельно заданному вектору
параллельно заданному вектору
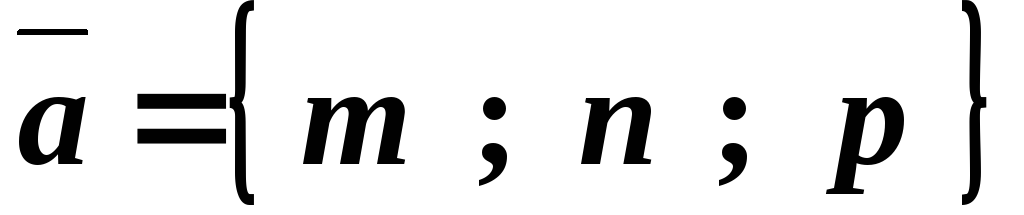
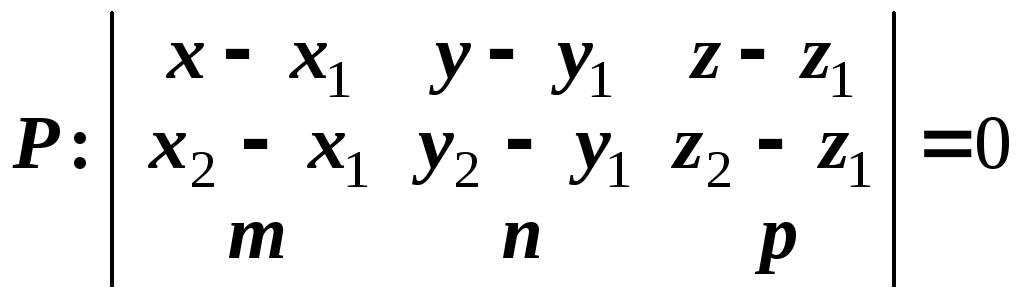 (18)
(18)
Пример
20.
Известно, что пространственная прямая
![]() ,
проходящая через точку
,
проходящая через точку![]() ,
пересекает плоскость
,
пересекает плоскость![]() в точке
в точке![]() .
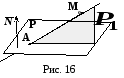
Найти уравнение плоскости
.
Найти уравнение плоскости![]() ,
проектирующей прямую
,
проектирующей прямую![]() на
данную плоскость
на
данную плоскость![]() (Рис. 16).
(Рис. 16).
 Решение.
Две точки, через которые проходит
искомая плоскость
Решение.
Две точки, через которые проходит
искомая плоскость
![]() ,
уже имеются
это точки
,
уже имеются
это точки
![]() и
и![]() .
По этим точкам можно ввести вектор
.
По этим точкам можно ввести вектор![]() ,
заведомо лежащий в искомой плоскости
,
заведомо лежащий в искомой плоскости![]() .
Далее, как всегда, введем точку
.
Далее, как всегда, введем точку![]()
произвольную точку искомой плоскости.
По ней и по точке, например,
произвольную точку искомой плоскости.
По ней и по точке, например,
![]() введем
еще один вектор, также лежащий в искомой
плоскости, а именно
введем
еще один вектор, также лежащий в искомой
плоскости, а именно![]() .
Осталось найти вектор, которому плоскость
.
Осталось найти вектор, которому плоскость![]() параллельна
или, что то же самое, который параллелен
этой плоскости. Таковым является вектор
параллельна
или, что то же самое, который параллелен
этой плоскости. Таковым является вектор![]()
нормальный вектор данной плоскости
нормальный вектор данной плоскости
![]() .
Введенные три вектора компланарны, а
значит их смешанное произведение
.
Введенные три вектора компланарны, а
значит их смешанное произведение![]() ,
что в координатах дает уравнение:
,
что в координатах дает уравнение:

![]() .
.
