§ 25.2 Спектры атомов. Спектральные серии. Формула Бальмера

Внутреннее строение атома изучать непосредственно невозможно из-за малости размеров атома, линейные размеры которого приблизи­тельно 10^-10 м. Структура атома проявляется только косвенно в явлениях, связанных с его внутренним строением. К числу этих явлений относится излучение.

При изучении излучения ученым удалось установить общие закономерности в характере спектров и найти ряд эмпирических законов, которым они подчиняются. Было установлено, что спектральные линии всех элементов можно разбить на ряд серий. Структуры соответствую­щих серий, относящихся к различным химическим элементам, схожи ме­жду собой. В пределах одной серии расположение спектральных линий имеет определенный порядок. Наиболее простым атомом является атом водорода.

Если с помощью призмы или дифракционной решётки разложить излучение атома водорода в спектр, то на экране будут различаться лишь отдельные цветные линии, разделённые широкими тёмными полосами. Спектр подобного вида называют линейчатым. Каждая линия этого спектра соответствует излучению определённой длины волны. А эти длины волн соответствуют тем частотам, на которых излучает атом водорода.

Возможные переходы электрона в атоме с одного энергетического уровня на другой условно разделяют на серии. Переходы электронов в атоме водорода из возбуждённых состояний на первый уровень образуют серию Лаймана, на второй уровень – серия Бальмера, на третий уровень – серия Пашена и так далее (рис.25.7).

В 1885 г. Бальмеру удалось найти формулу, описывающую распре­деление спектральных линий видимого спектра водорода, получивших название серии Бальмера:

(25.7)

[λ — длина волны; 1/ λ— волновое число; m – номер серии; n – номер спектральной линии в серии; R = 1,097 • 10⁷ м^-1 — постоянная Ридберга].

Определим энергию Е_n на любом энергетическом уровне. Для этого подставим в выражение полной энергии радиус орбиты:

(25.8)

При переходе электрона с одно­го энергетического уровня на другой, согласно второму постулату Бора, выделяется или поглощается квант энергии

ћω = |Е_n2-Е_n1|.

тогда

(25.9)

Если электрон переходит, напри­мер, со второй орбиты (n₂ = 2) на пер­вую (n₁= 1), то выделяется квант энергии. В обратном случае такой же квант энергии поглощается. Таким образом, максимальную энергию атому водорода нужно сообщить для того, чтобы перевести электрон на орбиту с n = 1 на n→ ∞, т. е. оторвать его от ядра атома (ионизовать атом).

Из соотношения (25.9) можно определить частоту ν или длину вол­ны λ = с/ν поглощаемого или ис­пускаемого фотона:

(25.10)

(25.11)

— сериальные формулы. Видно, что выражение (25.11) представляет со­бой обобщенную формулу Бальмера, а величина

(25.12)

является . ЗначениеR, вычисленное по формуле (25.12), совпадает с экспериментальным значением этой постоянной, что является подтверждением правильности теории Бора для атома водорода.

Теория Бора позволила объяснить и то, почему у атомов каждого химического элемента свой, совершенно определенный линейчатый спектр. Такая индивидуальность атомных спектров обусловлена тем, что у одинаковых атомов одинаковы и схемы расположения энер­гетических уровней.

У атомов же различных химических элементов разные схемы энер­гетических уровней, поэтому и линейчатые спектры у них тоже разные.

Существование дискретных энергетических состояний атомов яв­ляется одной из самых характерных особенностей их свойств, оно дока­зано многочисленными опытами.

Бора приводит к правильным результатам не только в случае атома водорода, но и в случае водородоподобных ионов, т. е. таких ионов, в которых вокруг ядра обращается только 1 элект­рон. Примерами таких ионов являются однократно ионизованные ато­мы гелия (Не⁺), дважды ионизованные атомы лития (Li⁺⁺) и т.д. Поскольку ядра этих ионов имеют заряд q =ze, то вместо е² в формуле теперь следует писать ze². Из-за этого радиус водородопо­добных ионов оказывается в z раз меньше, чем у атома водорода.

К водородоподобным атомам относят также системы, содержащие открытую в конце 30-х гг. частицу, называемую мюоном. Масса этой частицы примерно в 200 раз больше, чем у электрона, а заряд может быть как отрицательным (тогда эта частица обозначается μ^-, так и положительным (тогда она обозначается μ ⁺).

Задача 22. Как изменилась кинетическая энергия электрона в атоме при изменении фотона с длиной волны  = 486010^-10 м?

Решение.

Дано:  = 486010-10 м
к	Дж = 2,55 эВ

(1 эВ = 1,610^-19 Дж).

Задача 23. Найти энергию ионизации атома водорода (т.е. минимальную энергию, необходимую, чтобы оторвать электрон от атома).

Решение.

Дано: z = 1 n = 1	У водорода в нормальном состоянии z = 1, n = 1 и полная энергия электрона на первой орбите согласно (5)
Eион

Так как на большом удалении от ядра (на бесконечности) энергия электрона равна нулю, то для того, чтобы «поднять» электрон из потенциальной ямы (в которой он находится на «глубине» Е₁) до нулевого уровня, необходимо затратить энергию ионизации , т.е.

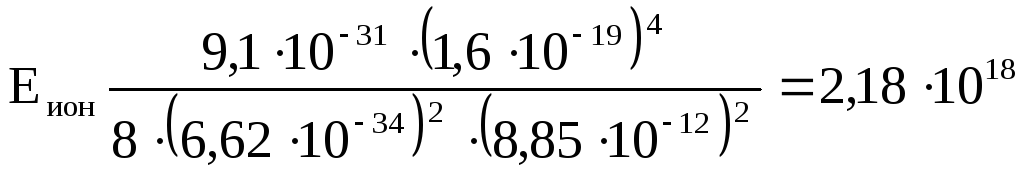Дж = 13,6 эВ.

Задача 24. Определить энергию, испускаемую при переходе электро6на в атоме водорода с третьей орбиты на первую.

Решение.

Дано: z = 1 n1 = 1 n2 = 3	По второму постулату Бора, энергия, испускаемая атомом при переходе электрона с третьей орбиты на первую, равна , где
	и

энергии электрона, находящегося на третьей и первой орбитах. Т.о.

.

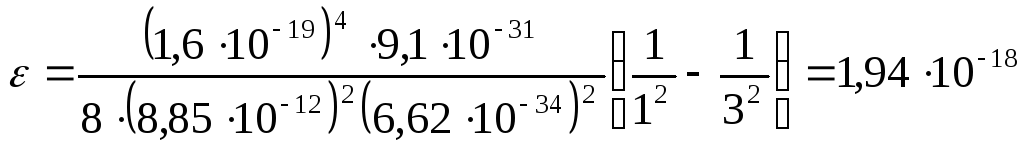Дж = 12,1 эВ.