Ранговые коэффициенты связи

Ранг - это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической от соответствующих номеров мест, которые определяют. Данные ранги называютсясвязными.

Предприятие	Балансовая прибыль, млн. руб.	Ранжирование (ранги)
1	10	6,5
2	12	4
3	10	6,5
4	12	4
5	12	4
6	15	2
7	17	1

Среди непараметрических методов оценки тесноты связи наибольшее значение имеют ранговые коэффициенты Спирмена (ρ).

№ банка	Активы банка (млн. руб.), X	Ранг по x	№ банка	Прибыль банка (млн. руб.), У	Ранг по у	di	di2
9	191	1	9	3,4	1	0	0
6	104	2	5	4,0	2	-6	36
5	109	3	7	6,4	3	1	1
8	113	4	8	10,1	4	0	0
4	185	5	3	12,7	5	-2	4
3	207	6	10	13,4	6	1	1
7	327	7	4	14,9	7	4	16
2	328	8	6	15,5	8	-1	1
10	849	9	2	17,8	9	3	9
1	866	10	1	39,6	10	0	0

Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывается по формуле (для случая, когда нет связных рангов):

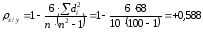
где d_i - квадрат разности рангов;

n - число наблюдений (число пар рангов).

По таблице «Значение коэффициентов корреляции рангов Спирмена» определяется при объеме выборки 10 единиц (i= 10) и уровне значимости 5% критическая величина для рангового коэффициента корреляции. Она составляет + 0,6364.

Поэтому общий выводпо результату анализа: есть необходимость увеличивать объем выборки.

Коэффициент конкордации — характеристика связи между несколькими признаками, измеренными по порядковой шкале. Этот коэффициент вычисляется по формуле: ,

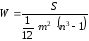где S — сумма квадратов отклонений суммы рангов каждого объекта от средней суммы рангов;

m — количество порядковых переменных;

n — объем выборки.

Коэффициент принимает значения от 0 до 1, т.е. 0 < W< 1. По своей сути коэффициент конкордации — среднее значение из коэффициентов ранговой корреляции Спирмена между каждой парой рангов. Число таких коэффициентов равно числу сочетаний из т по 2.

Значениям каждой переменной приписываются ранги. Ранг 1 устанавливается наименее важному значению: минимальному — для стимулянт, т.е. для переменных типа «чем больше, тем лучше», и максимальному для дестимулянт, т.е. для переменных типа «чем больше, тем хуже». Если нельзя отдать предпочтение нескольким объектам, то каждому из них присваивается средний ранг, определяемый как средний арифметический из суммы соответствующих мест («связанные ранги»). Скажем, если нельзя отдать предпочтение второму, третьему и четвертому объектам, то каждому из этих объектов присваивается ранг, равный=3,5. Связанные ранги могут быть и дробными.

Значимость W проверяется на основе критерия χ²: .

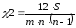Полученное значение должно быть не меньше критического (теоретического).

Знаменатель коэффициента конкордации представляет гипотетическую сумму рангов, получаемую в случае их полной согласованности. Чаще всего коэффициент конкордации используется для измерения согласованности мнений экспертов о влиянии различных признаков на результативную переменную.

Пример. Три эксперта дали характеристику разведанного месторождения газа по пяти признакам:

Признак	Эксперты			Сумма рангов по каждому признаку	Квадрат отклонения от средней суммы рангов
	1-й	2-й	3-й
Мощность месторождения	5	3	5	13	16
Трудности разработки	1	5	4	10	1
Наличие трудовых ресурсов	4	4	3	11	4
Потребность в оборудовании	3	1	2	6	9
Развитие транспортных коммуникаций	2	2	1	5	16
Итого	15	15	15	45	46
В среднем	3	3	3	9

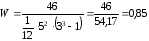, т.е. согласованность мнений экспертов довольно высокая.

Можно оценить значимость коэффициента конкордации по критерию χ²: .

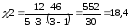Теоретическое значение χ² находится функцией ХИ2ОБР при вероятности 0,05 (5%) и количестве степеней свободы n-1 = 3-1=2 равно 5,99, то можно сделать вывод, что полученное значение коэффициента конкордации статистически значимо.