§ 4. Множественная регрессия

Множественная регрессия занимается изучением связи между результативным признаком и двумя и более факторными.

Множественная регрессия определяет:

1) форму связи;

2) тесноту связи;

3) влияние отдельных факторов на общий результат.

Определение формы связисводится обычно к отысканию уравнения связиус факторамих₁,х₂,х₃,...,х_n. Так, линейное уравнение зависимости результативного признака от двух и более факторных определяется по формуле:

Y=a₀ + a₁x₁ + a₂x₂+a₃x₃+…a_nx_n

Алгоритм выполнения индивидуального задания 3

Пакет анализа представляет собой надстройку (вспомогательную программу, служащую для добавления в Microsoft Office специальных команд или возможностей). Чтобы использовать надстройку в Excel, необходимо сначала загрузить ее.

4. Выберите кнопку «Office» …Параметры Excel… Надстройки.

5. Щёлкните по кнопке «Перейти».

6. В раскрывшемся окне активируйте опцию «Пакет анализа».

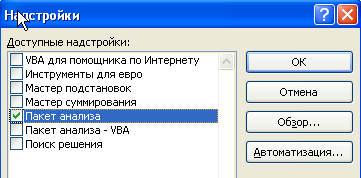
5. ОК

6. В меню «Данные» появляется надстройка «Анализ данных».

В ней представлен список методов статистической обработки данных:

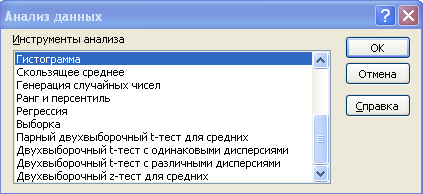
1. Рассчитайте коэффициенты корреляции (тесноту связи) между отдельными факторами, используя надстройку Пакет анализа.

1. Откройте файл «Задание для корреляционно-регрессионного анализа», выполненный в Excel.

2. Удалите из списка суммарные данные по округам и Российской Федерации в целом.

3. Выберите меню Данные, Анализ данных, Корреляция.

1. Поместите курсор в окно Входной интервал и обведите мышью все столбцы с данными, включая и заголовки столбцов.

2. Активизируйте опцию Метки в первой строке (если заголовки столбцов не включены, то метки не активизируются).

3. В Параметрах ввода активизируйте опцию Новый рабочий лист.

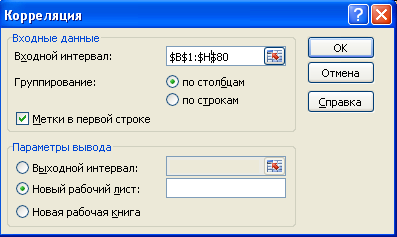
4. ОК.

5. В результате на отдельном листе выводится единичная симметричная матрица

В ней представлены коэффициенты корреляции между всеми факторами. Дайте интерпретацию коэффициентам корреляции, например:

1. связь между Валовым региональным продуктом и Средней начисленной заработной платой, а также Денежными доходами на душу населения и Объёмом промышленного производства– сильная;

2. между Валовым региональным продуктом и Оборотом розничной торговли – заметная;

3. между Оборотом розничной торговли и Денежными доходами на душу населения сильная, более 0,8;

4. связь между Выявленными правонарушениями и остальными факторами отсутствует.

7. Если связь между независимымипеременными тесная, т.е. если коэффициент корреляции превышает 0,8, то такие независимые переменные называютсямультиколлинеарными.

Это означает, что отобранные для анализа независимые факторы совместно воздействуют на общий результат. Эта связь затрудняет оценивание параметров регрессии. Поскольку одним из условий нахождения уравнения множественной регрессии является независимость действия факторов, коллинеарность факторов нарушает это условие. Если факторы модели коллинеарны, то они дублируют друг друга иодин из них рекомендуется исключить из регрессии. Предпочтение в этом случае отдается не фактору, более сильно связанному с результатом, а фактору, который при сильной связи с результатом имеетнаименьшуютесноту связи с другими факторами. В этом условии проявляется специфика множественной регрессии как метода исследования комплексного влияния факторов на результат в условиях их независимости друг от друга.

Например, при изучении зависимости у = f(x, z, v) матрица парных коэффициентов корреляцииоказалась следующей:

	Y	x	z	v
Y	1
x	0,8	1
z	0,7	0,8	1
v	0,6	0,5	0,2	1

Факторы хиz дублируют друг друга, т.к. связь между ними сильная (больше 0,7). В анализ нужно включить факторz, а нех, хотя корреляцияzс результатомуслабее, чем корреляция факторахсу, но значительно слабее межфакторная связьRzv(0,2) <Rxv(0,5). Поэтому в приведённом примере в уравнение множественной регрессии включаем факторыz,v.

В решаемой нами задаче исключим фактор Оборот розничной торговли.

2. Рассчитайте множественный коэффициент корреляции, коэффициент детерминации и коэффициенты множественной регрессии.

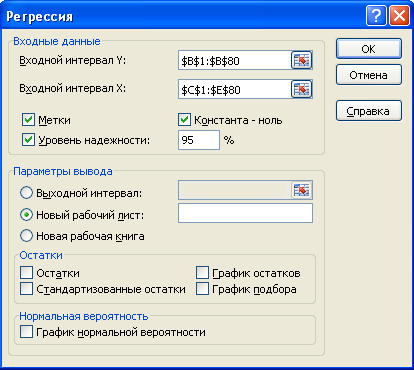
1. Выберите меню Данные, Анализ данных, Регрессия.

2. Поместите курсор в окно Входной интервал Yи обведите мышью столбец с данными, результативного признака (Валовым региональным продуктом), включая и заголовок столбца.

3. Поместите курсор в окно Входной интервал Xи обведите мышью все столбцы с данными факторных признаков, включая и заголовки столбцов.

4. Активизируйте опцию Метки в первой строке.

5. Опция Уровень надёжности по умолчанию настроена на 5% ошибку. Если потребуется другая точность вычисления, следует указать её.

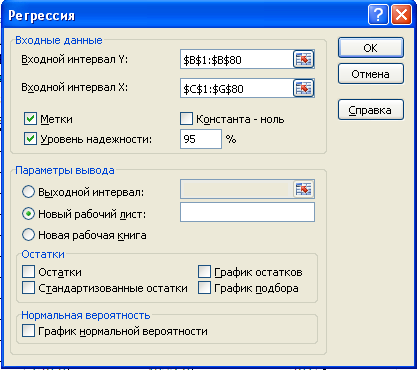
6. ОК

7. На новом листе отображается таблица:

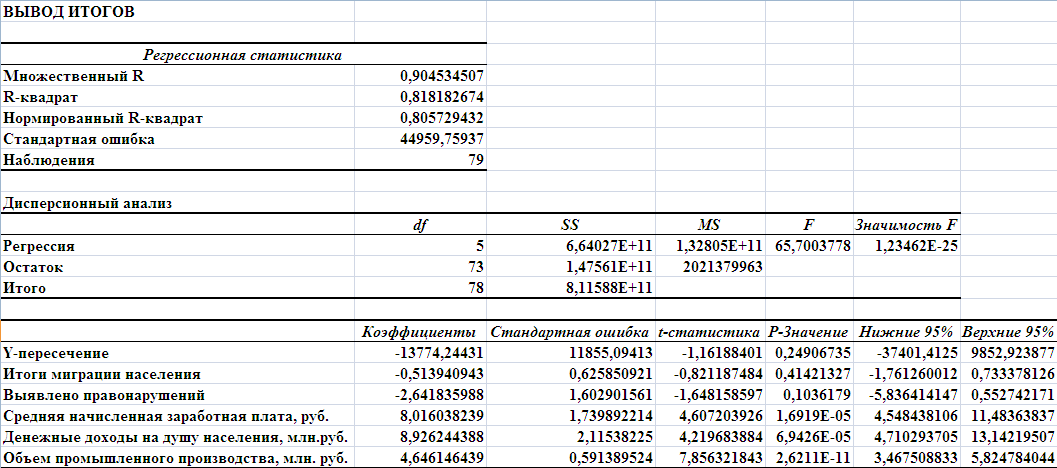
8. В таблице Регрессионная статистикасгенерированы результаты по регрессионной статистике. Эти результаты соответствуют следующим статистическим показателям:

• Множественный R - коэффициенту корреляции R;

• R-квадрат — коэффициенту детерминации R²;

• Стандартная ошибка — остаточному стандартному отклонению

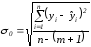
• Наблюдения — числу наблюдений п.

9. В таблице Дисперсионный анализ сгенерированы результаты дисперсионного анализа, которые используются для проверки значимости коэффициента детерминацииR-квадрат.

10. Столбцы имеют следующую интерпретацию:

11. Столбец df — число степеней свободы.

1. Для строки Регрессия число степеней свободы определяетсяколичеством факторных признаков m в уравнении регрессии k_ф=m=5.

2. Для строки Остаток число степеней свободы определяется числом наблюденийn и количеством переменных в уравнении регресси: k_о = п - (m+1)=79 – 6=73.

3. Для строки Итого число степеней свободы определяется суммой k_Y = k_Ф + k_о=5+73=78.

12. Столбец SS — сумма квадратов отклонений.

1. Для строки Регрессия — это сумма квадратов отклонений теоретических данных от среднего:

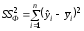
2. Для строки Остаток - это сумма квадратов отклонений эмпирических данных от теоретических:

3. Для строки Итого — это сумма квадратов отклонений эмпирических данных от среднего: 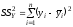или

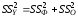
13. Столбец MS - дисперсии, рассчитываемые по формуле:

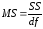
1. Для строки Регрессия - это факторная дисперсия.

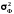2. Для строки Остаток - это остаточная дисперсия.

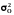14. Столбец F - расчетное значение F-критерия Фишера вычисляемое по формуле

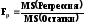
14. Столбец Значимость F- значение уровня значимости соответствующее вычисленному значениюFp. Определяется с помощью функции

FPACП (F_p; df(регрессия);df(остаток)).

Поскольку Значимость F = 1,23462E-25 меньше F= 65,7003778, уравнение регрессии значимо.

14. В следующей таблице сгенерированы значения коэффициентов регрессии а_i,- и их статистические оценки.

Столбцы имеют следующую интерпретацию:

1. Коэффициенты — значения коэффициентов а_i.

1. Стандартная ошибка — стандартные ошибки коэффициентов a_i

2. t-статистика — расчетные значения t-критерия, вычисляемые по формуле

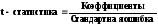
5. Р-значение - значения уровней значимости, соответствующие вычисленным значениям t_p. Определяются с помощью функции

=СТЬЮДРАСП(tp;n-m-1).

6. Нижние 95 % и Верхние 95 % — соответственно нижние и верхние границы доверительных интервалов для коэффициентов регрессии. Для нахождения границ доверительных интервалов с помощью функции = СТЬДРАСПОБР (tp; n – т - 1) рассчитывается критическое значение t-критерия t_кp, а затем по формулам

Нижние 95% = Коэффициент - Стандартная ошибка*t_кр;

Верхние 95% = Коэффициент + Стандартная ошибка*t_кр.

вычисляются соответственно нижние и верхние границы доверительных интервалов.

14. Анализ сгенерированных таблиц.

1. Рассчитанные ячейки коэффициенты регрессии а_i,- позволяют построить уравнение, выражающее зависимость Валового регионального продукта на душу населения Y от величины Итогов миграции населения X₁ , Количества правонарушений Х₂, Средней начисленной заработной платы, руб. Х₃, Денежных доходов на душу населения, млн.руб. Х₄, Объема промышленного производства, млн. руб. Х₅:

ŷ=-13774,24 - 0,51X₁- 2,64Х₂ + 8,01Х₃+ 8,93Х₄ + 4,65Х₅

2. Значение множественного коэффициента детерминации R² = 0,818182674 показывает, что 81,82 % общей вариации результативного признака объясняется вариацией факторных признаков Х₁, Х_2, Х_3, Х₄, Х₅, а на 18,18 % другими неучтёнными факторами. Значит, выбранные факторы существенно влияют на прибыль предприятий, что подтверждает правильность их включения в построенную модель.

Рассчитанный уровень значимости 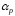=1,23462E-25 < 0,05 (показатель Значимость F) подтверждает значимость R².

3. Следующим этапом является проверка значимости коэффициентов регрессии: а₀, а_1…а₅.

Сравнивая попарно элементы массивов Коэффициенты и Стандартная ошибка, видим, что коэффициент регрессии а₁= -0,513940943 по абсолютной величине меньше, чем его стандартная ошибка = 0,625850921. Таким образом, фактор X₁ следует исключить из уравнения регрессии.

Стандартные ошибки остальных коэффициентов а_i меньше своих стандартных ошибок. Но не все они являются значимыми, о чем можно судить по значениям показателя Р-значение, которые должны быть меньше заданного уровня значимости α = 0,05. Таким незначимым является свободный член уравнения регрессии (коэффициент в строке Y-пересечение), его значимость 0,24906735 больше 0,05 и фактор X₂ (Выявлено правонарушений) 0,1036179.

4. Подводя итог предварительному анализу уравнения регрессии, можно сделать вывод, что его целесообразно пересчитать без фактора X₁, и X₂, и свободного члена, которые не является статистически значимыми. В диалоговом окне Регрессия необходимо задать новые параметры, и следует активизировать флажок Константа-ноль (для исключения свободного члена).

18. Пересчитывая значения уравнения регрессии без свободного члена, а также фактора Х₁ и Х₂

получаем следующую таблицу:

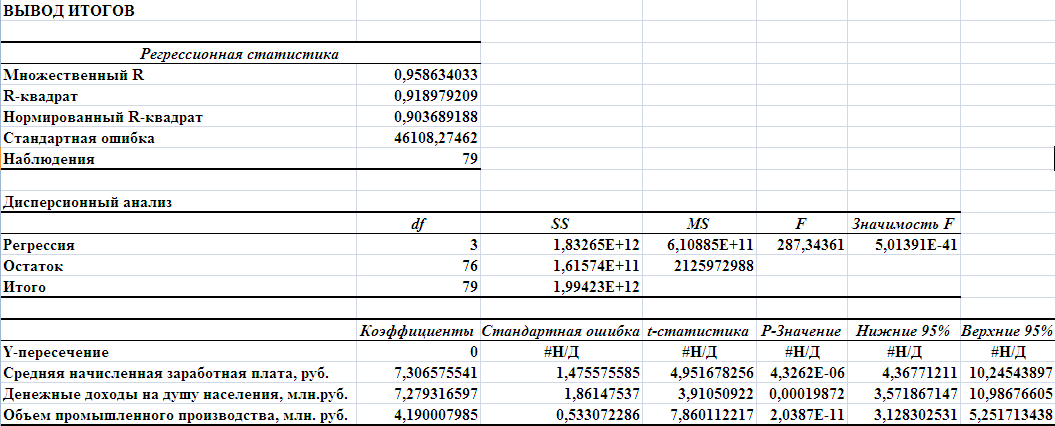
18. Сравнивая попарно элементы массивовКоэффициентыиСтандартная ошибка, видим, что абсолютные значения факторова_iбольше, чем их стандартные ошибки. К тому же эти коэффициенты являются значимыми, о чем можно судить по значениям показателя Р-значение, которые меньше заданного уровня значимостиα = 0,05. Значения #Н/Д в строкеY-пересечение, означает отсутствие свободного члена в уравнении регрессии.

19. Таким образом, получаем новое уравнение регрессии:

ŷ=7,31Х₄ + 7,28Х₅+ 4,19Х₆

18. Экономическая сущность коэффициентов а_i в полученном уравнении регрессии состоит в том, что они показывают степень влияния каждого фактора на результативный признак (Внутренний региональный продукт на душу населения). Так, увеличение Средней начисленной заработной платы на 1 рубль ведет к ведёт в увеличению Внутреннего регионального продукта на душу населения на 7,31 руб., увеличение Денежных доходов населения на 1 млн. руб. ведет к росту Внутреннего регионального продукта на душу населения на 7,28 руб., увеличение Объёма промышленного производства на 1 млн. рублей ведет к росту Внутреннего регионального продукта на душу населения на 4,19 руб.

3. Рассчитайте частные коэффициенты эластичности

С целью расширения возможностей экономического анализа используются частные коэффициенты эластичности, определяемые по формуле: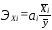

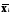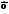где — среднее значение соответствующего факторного признака;— среднее значение результативного признака; a_i— коэффициент регрессии при соответствующем факторном признаке.

Коэффициент эластичности показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на 1%. Для нашего примера:

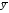= 122352,4861; 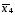=6964,983544; 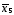=5857,824051; 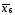=7995,178481.

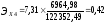
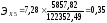
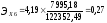
Это значит, что увеличение Средней начисленной заработной платы на 1 % ведет к ведёт в увеличению Внутреннего регионального продукта на душу населения на 0,42%, увеличение Денежных доходов населения на 1 % ведет к росту Внутреннего регионального продукта на душу населения на 0,35 %, увеличение Объёма промышленного производства на 1 % ведет к росту Внутреннего регионального продукта на душу населения на 0,27 %.