Угол
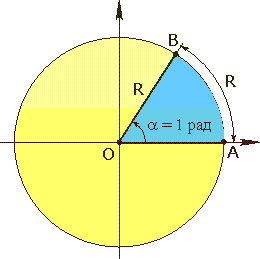
величиной в 1 радиан
1
радиан —
величина центрального угла окружности,
опирающегося на дугу, длина которой
равна радиусу этой окружности.
Примечание.
Очевидно, что угол в
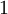 радиан
не меняется при переходе к другой
окружности. Измерение углов радианами
— пропорциональное, аналогичное
измерению градусами или измерению
отрезков единичными отрезками. Например,
угол опирающийся на дугу, длина которой
равна двум радиусам, будет иметь меру
радиан
не меняется при переходе к другой
окружности. Измерение углов радианами
— пропорциональное, аналогичное
измерению градусами или измерению
отрезков единичными отрезками. Например,
угол опирающийся на дугу, длина которой
равна двум радиусам, будет иметь меру
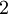 радиана.
радиана.
Радианная
мера угла, то
есть, выражение величины угла в радианах,
имеет преимущества перед градусной
мерой или любой другой: численное
значение радианной меры дуги единичной
окружности совпадает с длиной
соответствующей дуги.
Таким образом, радианная мера даёт
возможность отождествить
(не различать) измерение углов и отрезков.
Перевод
из градусной меры в радианную
Центральный
угол окружности, равный
 ,
опирается на полуокружность. Длина
полуокружности единичного радиуса
равна
,
опирается на полуокружность. Длина
полуокружности единичного радиуса
равна
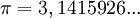 .
Следовательно,
.
Следовательно,
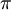 рад
рад
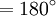 .
В силу принципа пропорциональности
радианной меры, получаем формулу для
перевода градусной меры произвольного
угла в радианную:
.
В силу принципа пропорциональности
радианной меры, получаем формулу для
перевода градусной меры произвольного
угла в радианную:
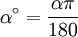 рад.
рад.
Пример.
Дан угол
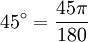 рад
рад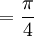 рад.
рад.
Перевод
из радианное меры в градусную
Центральный
угол окружности, равный
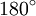 ,
опирается на полуокружность. Длина
полуокружности единичного радиуса
равна
,
опирается на полуокружность. Длина
полуокружности единичного радиуса
равна
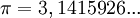 .
Следовательно,
.
Следовательно,
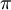 рад
рад
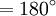 .
В силу принципа пропорциональности
радианной меры, получаем формулу для
перевода градусной меры произвольного
угла в радианную:
.
В силу принципа пропорциональности
радианной меры, получаем формулу для
перевода градусной меры произвольного
угла в радианную:
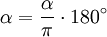 .
.
Пример.
Дан угол
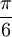 рад.
Выразить его величину в градусах.
рад.
Выразить его величину в градусах.
Решение.
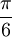 рад
рад
 .
.
|
Определение
и графики тригонометрических функций
|
|
|
|
Величины углов
(аргументы функций): α,
x
Тригонометрические функции: sin α,
cos α,
tan α,
cot α,
sec α,
cosec α
Множество
действительных чисел: ℜ
Координаты точки окружности: x,
y
|
Радиус круга:
r
Целые числа: k
|
-
Тригонометрические
функции
представляют собой элементарные
функции, аргументом которых является
угол.
С помощью тригонометрических функций
описываются соотношения между
сторонами и острыми углами в
прямоугольном треугольнике. Области
применения тригонометрических функций
чрезвычайно разнообразны. Так,
например, любые периодические процессы
можно представить в виде суммы
тригонометрических функций (ряда
Фурье). Данные функции часто
появляются при решении дифференциальных
и функциональных уравнений.
-
К
тригонометрическим функциям относятся
следующие 6 функций: синус,
косинус,
тангенс,
котангенс,
секанс
и косеканс.
Для каждой из указанных функций
существует обратная
тригонометрическая функция.
-
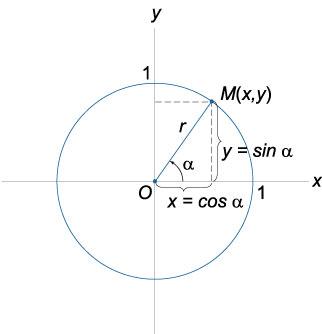
Геометрическое
определение тригонометрических
функций удобно ввести с помощью
единичного
круга. На
приведенном ниже рисунке изображен
круг радиусом r
= 1. На окружности обозначена точка
M(x,y).
Угол между радиус-вектором OM
и положительным направлением оси Ox
равен α.
-
Синусом
угла α
называется отношение ординаты y
точки M(x,y)
к радиусу r:
sin α
= y/r.
Поскольку r
= 1, то синус равен ординате точки
M(x,y).
-
Косинусом
угла α
называется отношение абсциссы x
точки M(x,y)
к радиусу r:
cos α
= x/r
= x
-
Тангенсом
угла α
называется отношение ординаты y
точки M(x,y)
к ee абсциссе x:
tan α
= y/x,
x
≠ 0
-
Котангенсом
угла α
называется отношение абсциссы x
точки M(x,y)
к ее ординате y:
cot α
= x/y,
y
≠ 0
-
Секанс
угла α
− это отношение радиуса r
к абсциссе x
точки M(x,y):
sec α
= r/x
= 1/x,
x
≠ 0
-
Косеканс
угла α
− это отношение радиуса r
к ординате y
точки M(x,y):
cosec α
= r/y
= 1/y,
y
≠ 0
-
В
единичном круге проекции x,
y
точки M(x,y)
и радиус r
образуют прямоугольный треугольник,
в котором x,
y являются
катетами, а r
− гипотенузой. Поэтому, приведенные
выше определения тригонометрических
функций в приложении к прямоугольному
треугольнику формулируются таким
образом:
Синусом
угла α
называется отношение противолежащего
катета к гипотенузе.
Косинусом
угла α
называется отношение прилежащего
катета к гипотенузе.
Тангенсом
угла α
называется противолежащего катета
к прилежащему.
Котангенсом
угла α
называется прилежащего катета к
противолежащему.
-
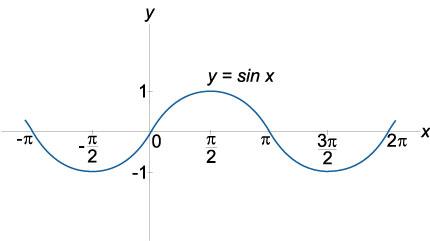
График
функции синус
y
= sin x,
область определения: x
∈
ℜ,
область значений: −1 ≤ sin x
≤ 1
-
График
функции косинус
y
= cos x,
область определения: x
∈
ℜ,
область значений: −1 ≤ cos x
≤ 1

-
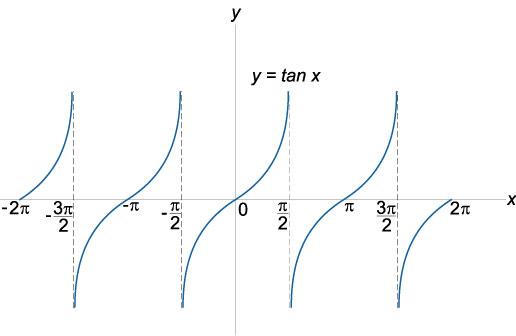
График
функции тангенс
y
= ttg
x,
область определения: x
∈
ℜ,
x
≠ (2k
+ 1)π/2,
область значений: −∞ < tg
x
< ∞
-
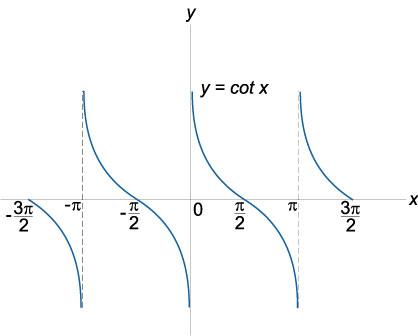
График
функции котангенс
y
= ctg
x,
область определения: x
∈
ℜ,
x
≠ kπ,
область значений: −∞ < ctg
x
< ∞
|
Формулы
приведения

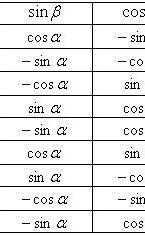
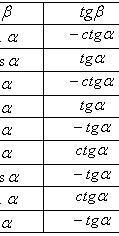
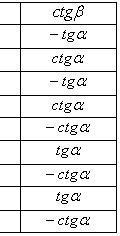
Основные
тригонометрические тождества
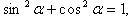
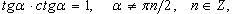
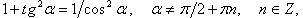
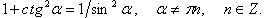


![]() радиан
не меняется при переходе к другой
окружности. Измерение углов радианами
— пропорциональное, аналогичное
измерению градусами или измерению
отрезков единичными отрезками. Например,
угол опирающийся на дугу, длина которой
равна двум радиусам, будет иметь меру
радиан
не меняется при переходе к другой
окружности. Измерение углов радианами
— пропорциональное, аналогичное
измерению градусами или измерению
отрезков единичными отрезками. Например,
угол опирающийся на дугу, длина которой
равна двум радиусам, будет иметь меру
![]() радиана.
радиана.
![]() ,
опирается на полуокружность. Длина
полуокружности единичного радиуса
равна
,
опирается на полуокружность. Длина
полуокружности единичного радиуса
равна
![]() .
Следовательно,
.
Следовательно,
![]() рад
рад
![]() .
В силу принципа пропорциональности
радианной меры, получаем формулу для
перевода градусной меры произвольного
угла в радианную:
.
В силу принципа пропорциональности
радианной меры, получаем формулу для
перевода градусной меры произвольного
угла в радианную:
![]() рад.
рад.
![]() рад
рад![]() рад.
рад.
![]() ,
опирается на полуокружность. Длина
полуокружности единичного радиуса
равна
,
опирается на полуокружность. Длина
полуокружности единичного радиуса
равна
![]() .
Следовательно,
.
Следовательно,
![]() рад
рад
![]() .
В силу принципа пропорциональности
радианной меры, получаем формулу для
перевода градусной меры произвольного
угла в радианную:
.
В силу принципа пропорциональности
радианной меры, получаем формулу для
перевода градусной меры произвольного
угла в радианную:
![]() .
.
![]() рад.
Выразить его величину в градусах.
рад.
Выразить его величину в градусах.
![]() рад
рад
![]() .
.




![]()
![]()
![]()
![]()





