1 Этап:

Находим максимальные интервалы данной функции. Их будет 4. Это четыре ребра: x₁ , x₁ x₂ , x₂ x₃ , x₃ .

Д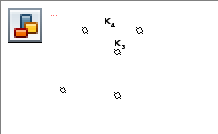ействительно, данные интервалы являются допустимыми и при удалении любого множителя получается интервал грань, а допустимых граней для данной функции нет. Других максимальных интервалов для данной функции также не существует.

Первый этап завершен.

2 Этап:

Найти все тупиковые покрытия.

; .

И других тупиковых покрытий нет.

Действительно, интервал обязан входить в любое покрытие , т.к. только он покрывает вершину 100. Интервалобязан входить в любое покрытие, т.к. только он покрывает вершину 001. Остаются два интервала;, из которых достаточно взять только один интервал , чтобы покрыть вершину 111. Сложность тупиковых покрытий одинакова. Это и есть все минимальные ДНФ данной функции.

Ответ:

Аналитический метод нахождения всех минимальных ДНФ функции.

I . Метод нахождения сокращенной ДНФ функции .

Метод будет проходить по этапам.

На начальном (нулевом) этапе рассматриваются все допустимые интервалы ранга n, т.е. СДНФ функции f . На этапе i ко всевозможным парам интервалов ранга (n-i) вида ;добавляется на интервалk (;).

Предыдущая операция называется склеиванием. После чего применяется операция поглощения: если есть пара интервалов;, то интервалудаляем. После этого переходим к очередному (i+1)–ому этапу. Если на этапеi операция склеивания не применима ни к каким интервалам, то алгоритм заканчивается и множество полученных интервалов и является в точности множеством всех максимальных допустимых интервалов.

Рассмотрим пример:

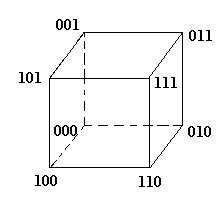
Этап 0.

; ;;;- поглощение.

Применяем операцию склеивания ко всевозможным интервалам.

(3-0)=3

1 и 2 , добавляем .

2 и 3, добавляем

2 и 4, добавляем

3 и 5, добавляем

4 и 5 , добавляем

После применения операции поглощения будут удалены все интервалы ранга 3.

, ,,,

Этап 1.

Имеем интервалы ранга 3-1=2 : ,,,,и применяем операцию склеивания .дадут интервал.

После применения операции поглощения получим интервалы : ;.

Этап 2.

Ко всем интервалам ранга 2-1=1 применяем операцию склеивания . В данном случае она не применима. Алгоритм завершает работу.

Все максимальные интервалы : ,

Корректность алгоритма .

Покажем, что действительно алгоритм находит все допустимые максимальные интервалы функции f.

Утверждение 1 : Все интервалы, которые возникают на этапах алгоритма являются допустимыми.

Действительно для интервалов на начальном этапе это утверждение справедливо, т.к. на начальном этапе рассматриваются допустимые интервалы максимального ранга.

Индуктивный базис .

Пусть интервал k возник в результате операции склеивания двух допустимых интервалов и. Тогда интервалk также является допустимым. Действительно, набор, на котором конъюнкция K равна 1 в компоненте, соответствующей переменной x может иметь произвольное значение 0 или 1, т. к. данная переменная не входит в множество переменных рассматриваемой конъюнкции K. Тогда, если в этой компоненте набор имеет единицу, то этот набор будет единицей конъюнкции , а если в рассматриваемой компоненте набор содержит 0, то тогда это есть единица конъюнкции. Т. е. единицы конъюнкции K принадлежат объединению единиц предыдущих двух конъюнкций. И в силу допустимости этих двух конъюнкций имеем.

Тогда справедливо , т. е. конъюнкцияK – допустимый интервал.

Утверждение 2: На входе i-ого этапа интервалы ранга (n-i) в точности все допустимые интервалы такого ранга, а интервалы большого ранга есть в точности все максимальные интервалы.

Докажем данное утверждение методом индукции.

На начальном (нулевом) этапе утверждение справедливо. Интервалы ранга n на этом этапе – это все допустимые конъюнкции ранга n функции f.

Допустим утверждение справедливо для этапа i, т. е. на входе этапа i содержатся все допустимые интервалы ранга (n-i), а интервалы большего ранга есть в точности все максимальные интервалы такого ранга.

Рассмотрим (i+1) этап и докажем справедливость утверждения для этого этапа.

Во-первых, покажем, что любой допустимый интервал ранга (n-(i+1)) содержится на входе этого этапа.

Рассмотрим такой допустимый интервал k, рассмотрим переменную x, которая не входит в конъюнкцию этого интервала. Тогда интервалы иявляются также допустимыми, т. к. любые единицы данных интервалов являются единицами допустимого интервала k.

Тогда в силу предположения индукции, эти два допустимых интервала ранга (n-i) содержатся на входе этапа i.

После применения операции склеивания к рассматриваемым интервалам и получается интервал k.

Во-вторых, покажем, что интервалы большего ранга, чем n-i-1 есть в точности все интервалы такого ранга.

Рассмотрим максимальный интервал ранга (n-i)k и покажем, что он будет содержатся на входе этапа i+1.

Действительно, как допустимый интервал ранга (n-i) по предположению индукции он содержался на входе этапа i. И этот интервал в силу своей максимальности не мог быть поглощенным ни одним из допустимых интервалов меньшего ранга n-i-1. А только допустимые интервалы возникают на этапах алгоритма.

Поэтому допустимый интервал k будет сохранен на этапе i и по этому будет содержатся на входе этапа (i+1).

Верно обратное утверждение, т. е. если интервал k ранга (n-i) содержится на входе i+1 этапа, то этот интервал максимальный.

Действительно, в силу доказанного данный интервал допустимый и поэтому содержится на входе этапа i, и не был поглощен на i-ом этапе. Но тогда все интервалы, которые получаются из данного интервала удалением какого-либо множителя будут недопустимыми, а поэтому данный интервал является максимальным. Поэтому доказано, что любой интервал ранга n-i является максимальным и наоборот любой максимальный ранга n-i содержится на входе i+1 этапа. Т. е. интервалы ранга n-i, есть в точности все максимальные интервалы такого ранга.

Для интервалов большего ранга, чем (n-i) утверждение о их максимальности следует из утверждения базиса индукции этапа i.

Ч.Т.Д.

Тогда из данного утверждения корректность алгоритма следует из справедливости утверждения для последнего этапа.

Метод нахождения всех тупиковых покрытий максимальными интервалами.

Мы представляем регулярный способ перечисления всх тупиковых покрытий посредством ограниченного перебора.

Рассмотрим таблицу покрытия. Пусть функция f (,…,) отn переменных имеет s единиц ,…,, иm максимальных интервалов ,…,. Таблица будет содержатьs столбцов, каждый столбец будет соответствовать определенной единице функции и будет содержать m строк , каждая строка соответствует определенному максимальному интервалу.

	,…	,…

На пересечении строки и столбца, который соответствует единице функциипоставим интервал, если интервал покрывает. И пусто, если интервал не покрывает единицу. Таким образом, в столбценепустые элементы в точности все максимальные интервалы, которые покрывают единицу.

Например,

K₂

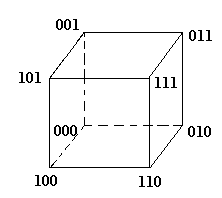
-передняя грань ,- ребро

	0	1	1	1	1
	1	1	1	0	0
	1	1	0	0	1

Определение: Выборкой называют упорядоченный набор интервалов

, ,…,,(каждый индекс принимает значения из множества чисел, причем значения некоторых индексов могут повторяться), чтоесть не нулевой элемент первого столбца , и т. д.,- ненулевой элемент последнегоs – того столбца .

Например :

 выборки.

Утверждение 1 : Интервалы любой выборки являются покрытием.

Рассмотрим произвольную выборку ,, … ,. Все интервалы данного множества допустимы, и все единицы функции покрыты.

Действительно, первая единица функции покрыта интервалом , вторая, и т. д., последняя единица покрыта.

Утверждение 2 : Взяв в некотором порядке некоторые интервалы покрытия, можно получить выборку.

Рассмотрим произвольное покрытие. Рассмотрим интервал, который покрывает первую единицу функции, обозначим его .

Рассмотрим и обозначим, который покрывает вторую единицу функции и т. д. Рассмотрим интервал, который покрывает последнююs – ую единицу функции.

Такие интервалы обязательно найдутся, потому что рассматриваемое множество является покрытием.

Тогда полученное множество интервалов ,, … ,является выборкой.

Из этих утверждений следует

Утверждение 3 : Множество тупиковых покрытий содержится среди выборок.

Действительно, каждое тупиковое покрытие есть выборка, которую оно содержит. Интервалы тупикового покрытия можно упорядочить, и при этом получим выборку.

Таким образом, чтобы найти множество тупиковых покрытий нужно найти множество всех выборок, исключить из них нетупиковые выборки.

Множество оставшихся выборок и есть требуемое множество тупиковых покрытий.

Таким образом, мы должны разработатьметод перечисления всех выборок и удаления нетупиковых выборок.

Метод нахождения всех выборок .

Пусть ,…,ненулевые элементы первого столбца в таблице покрытия.

,…, ненулевые элементы второго столбца в таблице покрытия .

…

,…, ненулевые элементы последнегоs – того столбца в таблице покрытия.

Рассмотрим функцию покрытия . Это есть КНФ от переменных, которые соответствуют максимальным интервалам таблицы покрытия.

Это КНФ есть произведение по всем столбцам покрытия , где каждому столбцу соответствует множитель равный дизъюнкции ненулевых элементов

(…)(…)…(…).

	1	1	1	0	0
	0	0	1	1	1
	0	1	1	1	0

Пример: максимальные интервалы- есть следующие ребра

₂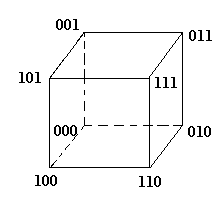

()()()()() - КНФ

Раскроем скобки в полученной КНФ , т.е. перейдем от КНФ к ДНФ .

Утверждение : Множество слагаемых полученной ДНФ и есть множество всевозможных выборок.

Действительно, каждое слагаемое при раскрытии скобок получается при выборе в первом множителе КНФ одного из интервалов, которые по построению покрывают первую вершину. Во втором множителе КНФ при выборе некоторого интервала, который по построению покрывает вторую вершину и т. д. В последнем множителе при выборе интервала, который по построению покрывает последнююs – тую вершину.

Полученное множество интервалов есть выборка.

Множество всевозможных таких слагаемых и есть множество всех выборок.

После нахождения всех выборок удаляем нетупиковые выборки. Выборка будет нетупиковой, если из нее можно удалить некоторые интервалы так, что все равно получится выборка.

Т. е. по-другому говоря, слагаемое, которое соответствует нетупиковой выборке поглощается слагаемым, которое соответствует тупиковой выборке.

Например :

Множество интервалов является выборкой.

- является выборкой .

Верхнее не является тупиковой, потому что при удалении интервала получается нижнее покрытие.

Т. е. интервал поглощает.

Таким образом, чтобы получить все тупиковые выборки нужно в построенной ДНФ применить все возможные поглощения.

Множество оставшихся слагаемых и будут всевозможные тупиковые покрытия .

Таким образом, переход от КНФ к ДНФ и есть требуемый метод перечисления всех выборок. Удаление нетупиковой выборки есть операция поглащения

.

Примечание : Операцию поглощения можно применять в процессе раскрытия скобок .

Корректность этой операции следует из примера. Раскрывая скобки, получаем

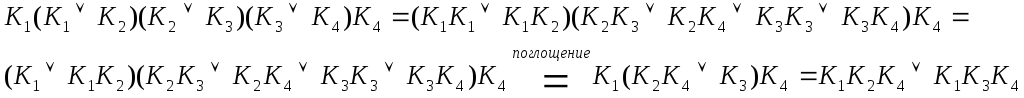
Мы применяем поглащение в процессе раскрытия скобок в силу того, что покрытия содержащие пару интервалов не будут тупиковыми- соответствующие слагаемое, которое будет содержать только будет короче.

Тупиковые покрытия максимальными интервалами:

;

Теперь нужно выбрать покрытия, которые обладают наименьшей сложностью. Оба покрытия имеют одну сложность, поэтому это и есть все минимальные ДНФ нашей функции. Сложность равна шести. Ответ минимальные ДНФ-

;