
- •Введение
- •Дискретная математика
- •Бинарная операция ассоциативна, если тождественно выполняется: ;
- •4.Классы булевых функций :
- •X1 x2 X
- •5. Теория полноты
- •I этап :
- •3 Случай :
- •II этап :
- •1); 2); 3); 4).
- •1) ; 2); 3);
- •4) ; 5);
- •5.4. Полные системы в классах т0, т1, м, s, l.
- •5.5 Базисы в классах t0 , t1, s, m, l Все полные системы для классов t0, t1, s, m, l в утверждениях выше являются базисами для этих систем.
- •6 .Минимизация булевых функций
- •1 Этап:
- •2 Этап:
- •Достаточно ясна связь задачи нахождения тупиковых покрытий и минимизации функции покрытия.
- •7. Исчисления высказываний
- •8. Семь теорем
- •Доказательство полноты исчисления высказываний.
- •Представление графов
- •1. Задание графа с помощью матрицы смежности.
- •2. Задание графа с помощью матрицы инцидентности.
- •3. Задание графа с помощью списка смежности.
- •Связные графы
- •Алгоритмы нахождения компонент связности
- •1. Поиск в ширину
- •2. Поиск в глубину
- •Укладки графов
- •Теорема Эйлера
- •Критерий Понтрягина-Куратовского
- •Раскраски графов
- •Основные понятия комбинаторики.
- •1 1.2 Упорядоченные наборы элементов изn-данных
- •1.3 Неупорядоченные наборы элементов изданных без повторений.
- •1.4 Неупорядоченные наборы элементов изп данных с возможными повторениями.
- •2 Метод включения-исключения.
- •Упражнения.
- •3 Метод производящих функций
- •1324 0100.
- •4 Основы теории перечисления Пойа. Лемма Бернсайда.
- •Упражнения.
- •Глава. Основы схем из функциональных элементов.
- •1) Мультиплексор порядка
- •2) Дешифратор порядка .
- •3) Универсальный многополюсник.
- •Глава. Введение в теорию конечных автоматов.
- •Глава. Введение в теорию кодирования.
- •Теория кодирования.
2 Метод включения-исключения.
Пусть
имеется множество элементов
![]() и пусть имеется множество свойств
и пусть имеется множество свойств![]() ,
которыми элементы
,
которыми элементы![]() могут
обладать или нет. Пусть
могут
обладать или нет. Пусть![]() —
число элементов, обладающих свойствами
—
число элементов, обладающих свойствами
![]() .
Пусть
.
Пусть
![]() обозначает
число
элементов,
обладающих ровно
обозначает
число
элементов,
обладающих ровно
![]() свойствами.
свойствами.
Теорема.
![]() =
=![]()
Доказательство.
1.
Рассмотрим элемент
![]() обладающий
ровно
обладающий
ровно![]() свойствами. Такой элемент войдет в
свойствами. Такой элемент войдет в![]() только при
только при![]() и в сумме
и в сумме![]() будет
считаться
единственный раз. Поэтому элементы,
обладающие
ровно
будет
считаться
единственный раз. Поэтому элементы,
обладающие
ровно
![]() свойствами, будут входить в сумму по
одному разу.
свойствами, будут входить в сумму по
одному разу.
2.
Рассмотрим элемент![]() обладающий ровно
обладающий ровно![]() свойствами,
свойствами,![]() .Тогда
в
.Тогда
в![]() они
будут входить при
они
будут входить при![]() а в
а в![]() они войдут
они войдут![]() раз. Тогда общее число вхождений такого
элемента
раз. Тогда общее число вхождений такого
элемента![]() есть
есть
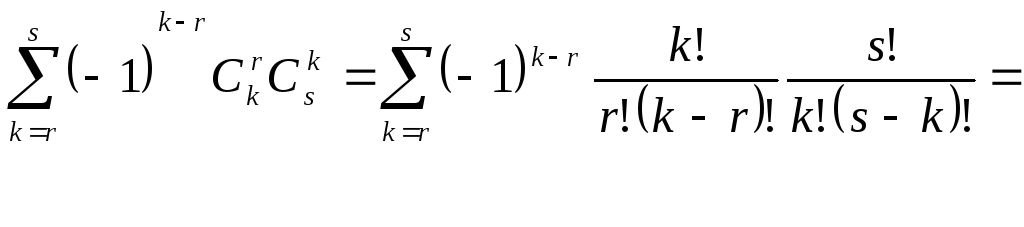
![]()
![]()
Таким образом, из 1 и 2 следует требуемое свойство.
Пример
1.
Подсчитать число перестановок, оставляющих
на месте ровно
![]() элементов.
элементов.
Решение.
Вводим множество всех перестановок
![]() элементов
элементов![]() .
Вводимn
свойств
.
Вводимn
свойств
![]() :
:![]() -тый
элемент при перестановке
-тый
элемент при перестановке![]() остается
на месте. Тогда число перестановок,
оставляющих на месте ровно
остается
на месте. Тогда число перестановок,
оставляющих на месте ровно![]() элементов, есть:
элементов, есть:![]()
где
N(![]() )
— число перестановок, оставляющих на
месте
)
— число перестановок, оставляющих на
месте
![]() -ый,
-ый,![]() -ой,…,
-ой,…,![]() -ый
элементы, и это число есть очевидно,(n-k)!,
а число слагаемых в сумме
-ый
элементы, и это число есть очевидно,(n-k)!,
а число слагаемых в сумме![]() есть
есть![]() .
Поэтому
искомое
число есть
.
Поэтому
искомое
число есть
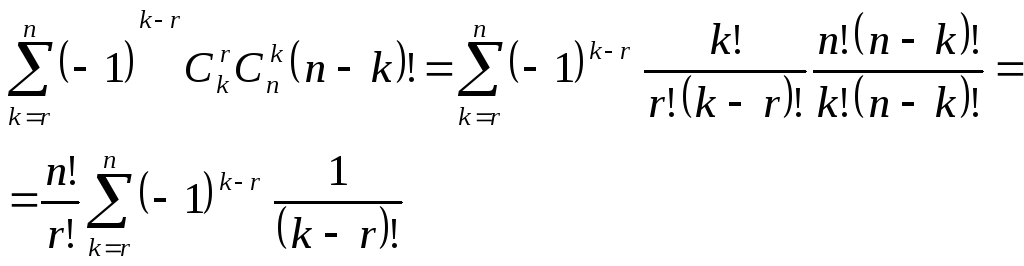
Здесь
![]()
И
при больших
![]() получим ассимтотическую формулу
получим ассимтотическую формулу![]()
Пример
2.
Найти число чисел взаимно простых с
данным
![]() .
Обозначим это число через
.
Обозначим это число через![]() (так называемая функция Эйлера).
(так называемая функция Эйлера).
Решение.
Введем множество натуральных чисел 1,
2,..., т
и
введем
свойства
![]() ,
где
,
где![]() означает, что число делится на простое
число
означает, что число делится на простое
число![]() .
Тогда числа взаимно простые с т
есть числа, которые не обладают ни одним
из свойств
.
Тогда числа взаимно простые с т
есть числа, которые не обладают ни одним
из свойств
![]() ,
т.е. обладают 0 свойствами, и поэтому
искомое число есть
,
т.е. обладают 0 свойствами, и поэтому
искомое число есть
![]()
где
![]() есть
число чисел, делящихся
на
есть
число чисел, делящихся
на
![]() ,
и поэтому это числа, представленные в
виде
,
и поэтому это числа, представленные в
виде
![]()
где
множитель h
изменяется 1,2,![]() Поэтому
Поэтому
![]() =
=![]()
и
тогда
![]() =
=![]()
![]() =
=
![]()
![]()
![]()
Пример
3.
Найти число способов раскладки m
различных шаров по n
различным урнам, при которых ровно
![]() урн пусты.
урн пусты.
Решение.
Введем множество различных раскладок
m
различных шаров по n
различным
урнам, т.е. упорядоченных наборов m
элементов из множества {1,2,..., n}
n-элементов
с возможными повторениями. Введем
свойства раскладок![]() .
.![]() —i-ая
урна пуста. Тогда искомое число есть
—i-ая
урна пуста. Тогда искомое число есть![]() —
ровно
—
ровно
![]() урн
пусты.
урн
пусты.
![]()
![]() — число
раскладок, при которых
— число
раскладок, при которых
![]() ая,
ая,![]() ая,
ая,![]() ая
урны пусты и это число, как нетрудно
видеть, есть
ая
урны пусты и это число, как нетрудно
видеть, есть![]() .
Поэтому
.
Поэтому
![]()
Упражнения.
1.
Имеется колода карт четырех мастей по
n
карт
каждой масти. Берут
![]() карт. Найти число комбинаций, в которых
имеются все масти.
карт. Найти число комбинаций, в которых
имеются все масти.
2.
Бросают
![]() различных игральных кубиков.
Найти
число комбинаций, когда имеются все
цифры.
различных игральных кубиков.
Найти
число комбинаций, когда имеются все
цифры.
3.
Найти число квадратных двоичных матриц
размера n![]() n,
в каждой строке которых содержится хотя
бы один ноль.
n,
в каждой строке которых содержится хотя
бы один ноль.
4.
Найти число двоичных матриц размера
![]() n
в строках, которых содержатся все
двоичные слова длины m.
n
в строках, которых содержатся все
двоичные слова длины m.
5. Составляют n-значные числа из цифр 1,2,3,4. Найти число чисел, в
которых имеются все цифры.
3 Метод производящих функций
Пусть
имеется некоторая последовательность
целых положительных чисел:
![]()
Производящей
функцией
последовательности
![]() называют
формальный
ряд
называют
формальный
ряд
![]()
Пример
1.
Рассмотрим последовательность
![]() где
где![]() —
число неупорядоченных наборов без
повторений i
элементов из n
имеющихся.
Тогда
—
число неупорядоченных наборов без
повторений i
элементов из n
имеющихся.
Тогда
![]()
но,
с другой стороны, рассмотрим функцию
![]() и рас-
и рас-
кроем
в ней скобки, тогда коэффициент при
![]() есть число выборовi
скобок
из n
имеющихся,
в которых брали t,
а в остальных
1.
Таким
образом,
есть число выборовi
скобок
из n
имеющихся,
в которых брали t,
а в остальных
1.
Таким
образом,
![]() =
=![]()
Тогда
![]()
![]()
Пример
2.
Производящая функция последовательности
неупорядоченных наборов с повторениями
![]() где
где
![]() —
число неупорядоченных наборов с
возможными повторениями i
элементов из п
имеющихся,
—
число неупорядоченных наборов с
возможными повторениями i
элементов из п
имеющихся,
![]()
Но, с другой стороны, рассмотрим функцию
![]() и
раскроем в ней скобки, тогда коэффициент
при
и
раскроем в ней скобки, тогда коэффициент
при
![]() равен числу решений уравнения
равен числу решений уравнения![]()
в
целых числах, что и является числом![]() .
Поэтому
.
Поэтому
![]() =
=![]()
![]()
![]()
Пример
3.
Производящая функция последовательности
неупорядоченных наборов i
элементов
из n
данных,
где только первый элемент может
повториться
![]() раз
раз![]() .
.
![]()
В частности производящая функция последовательности неупорядоченных наборов, где только первый элемент может повторяться, есть
![]() =
=![]() .
.
![]()
![]()
![]()
![]()
![]()
Здесь во второй строке применена формула Лейбница для производной произведения.
Пример
4.
Производящая функция последовательности
перестановок из n
элементов
1,2,...
,п с
определенным числом инверсий
![]()
![]()
Вектором
инверсий
перестановки
![]() называют
n
-компонентный
вектор, где i-ая
его компонента равна числу
чисел
больших i,
стоящих левее i
в
перестановке
называют
n
-компонентный
вектор, где i-ая
его компонента равна числу
чисел
больших i,
стоящих левее i
в
перестановке
![]() .
.
