
- •Введение
- •Дискретная математика
- •Бинарная операция ассоциативна, если тождественно выполняется: ;
- •4.Классы булевых функций :
- •X1 x2 X
- •5. Теория полноты
- •I этап :
- •3 Случай :
- •II этап :
- •1); 2); 3); 4).
- •1) ; 2); 3);
- •4) ; 5);
- •5.4. Полные системы в классах т0, т1, м, s, l.
- •5.5 Базисы в классах t0 , t1, s, m, l Все полные системы для классов t0, t1, s, m, l в утверждениях выше являются базисами для этих систем.
- •6 .Минимизация булевых функций
- •1 Этап:
- •2 Этап:
- •Достаточно ясна связь задачи нахождения тупиковых покрытий и минимизации функции покрытия.
- •7. Исчисления высказываний
- •8. Семь теорем
- •Доказательство полноты исчисления высказываний.
- •Представление графов
- •1. Задание графа с помощью матрицы смежности.
- •2. Задание графа с помощью матрицы инцидентности.
- •3. Задание графа с помощью списка смежности.
- •Связные графы
- •Алгоритмы нахождения компонент связности
- •1. Поиск в ширину
- •2. Поиск в глубину
- •Укладки графов
- •Теорема Эйлера
- •Критерий Понтрягина-Куратовского
- •Раскраски графов
- •Основные понятия комбинаторики.
- •1 1.2 Упорядоченные наборы элементов изn-данных
- •1.3 Неупорядоченные наборы элементов изданных без повторений.
- •1.4 Неупорядоченные наборы элементов изп данных с возможными повторениями.
- •2 Метод включения-исключения.
- •Упражнения.
- •3 Метод производящих функций
- •1324 0100.
- •4 Основы теории перечисления Пойа. Лемма Бернсайда.
- •Упражнения.
- •Глава. Основы схем из функциональных элементов.
- •1) Мультиплексор порядка
- •2) Дешифратор порядка .
- •3) Универсальный многополюсник.
- •Глава. Введение в теорию конечных автоматов.
- •Глава. Введение в теорию кодирования.
- •Теория кодирования.
4.Классы булевых функций :
Функции сохраняющие ноль -T0 и функции
сохраняющие единицу- T1 .
T0
:
![]() T1:
T1:
![]()
![]() T0
,
T0
,
![]() T1
T1
![]() T0
,
T0
,
![]() T1
T1
![]() T0
,
T0
,
![]() T1
T1
![]() T0
,
T0
,
![]() T1
T1
![]() T0
,
T0
,
![]() T1
T1
![]() T0
,
T0
,
![]() T1
T1
![]() T0
,
T0
,
![]() T1
T1
![]() T0
,
T0
,
![]() T1
T1
Самодвойственные функции S .
Определение:
![]() называетсясамодвойственной,
если совпадает с двойственной к ней
функцией.
называетсясамодвойственной,
если совпадает с двойственной к ней
функцией.
![]() .
.
Очевидно эквивалентное определение самодвойственной функции:
Определение:![]() S,
если
принимает противоположные значения на
противоположных наборах.
S,
если
принимает противоположные значения на
противоположных наборах.
|
x1 |
x2 |
x3 |
f(x1x2x3)
|
|
0 |
0 |
0 |
1 |
|
|
0 |
1 |
0 |
|
|
1 |
0 |
1 |
|
|
1 |
1 |
1 |
|
|
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
Пример:
![]() S
S
![]() S
S
![]() S
S ![]() S
S
![]() S
S
![]() S
S
![]() S
S ![]() S
S
Монотонные функции M .
Определение:
набор
![]() ,
если
,
если![]() ;
;
Например:
![]()
наборы 0101 и 1001 не сравнимы.
Определение:
![]() M,
если
M,
если
![]() :
:
![]() .
.
y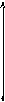








X1 x2 X
-
x1
x2
x3
f(x1x2x3)
 M
M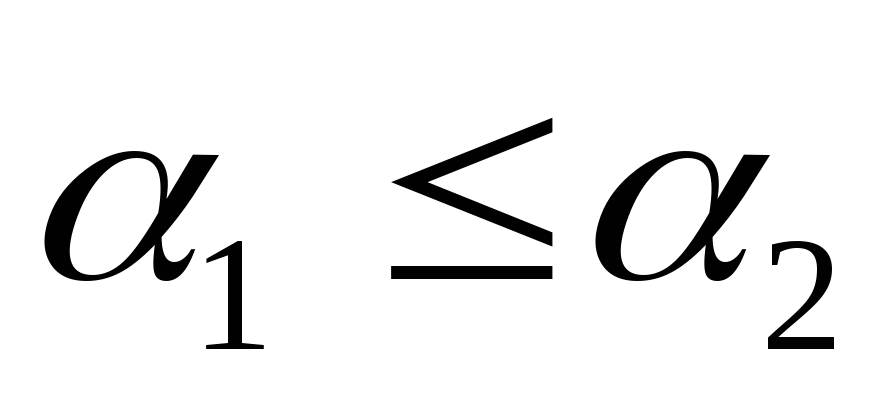
0
0
0
0
0
0
1
1
 0
01
0
0
0
1
1
1
 1
10
0
0
1
0
1
1
 1
11
0
1
 1
11
1
1
Метод определения монотонности функции f :
Рассматриваем
все наборы, на которых значение
![]() .
Для этих наборов рассматриваем наборы
большие, и если среди больших наборов
нет нуля функции, тогда функция монотонна.
В противном случае она не монотонная.
Корректность этого метода следует
непосредственно из определения монотонной
функции.
.
Для этих наборов рассматриваем наборы
большие, и если среди больших наборов
нет нуля функции, тогда функция монотонна.
В противном случае она не монотонная.
Корректность этого метода следует
непосредственно из определения монотонной
функции.
-
x1
x2
x3
f(x1x2x3)
 M
M0
0
0
0
0

0
1
1
0
1
0
0
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
1
Для данной функции для единицы 001 большие наборы есть 101, 011, 111. Среди них есть ноль, набор 011. Поэтому функция немонотонная.
![]() M
M
![]() M
M
![]() M
M
![]() M
M
![]() M
M
![]() M
M
![]() M
M
![]() M
M
Линейные функции L .
Определение: линейные функции – функции, степень полинома Жегалкина которых не больше единицы .
Определение: степенью полинома Жегалкина называется максимальное число переменных в слагаемых этого полинома.
Степень
![]() равна 3.
равна 3.
Степень
![]() равна 1.
равна 1.
Степень 1 равна 0 ; степень 0 равна 0.
-
 x1
x1x2
x3
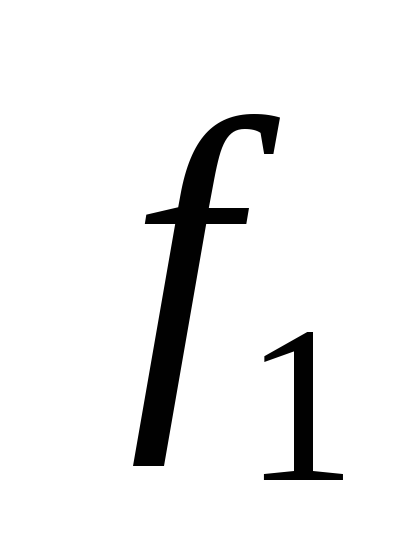

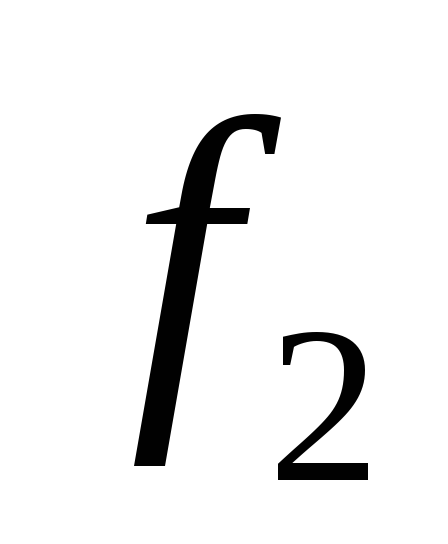
0
0
0
0
0
0
0
1
0
0
0
1
0
1
0
0
1
1
1
0
1
0
0
1
0
1
0
1
1
0
1
1
0
0
1
1
1
1
0
1
Методы определения линейности функции f :
1.Способ
Находим полином Жегалкина функции f
и определяем его степень. Если степень
![]() ,
то функция линейная. В противном случае
функция нелинейная.
,
то функция линейная. В противном случае
функция нелинейная.
2. Способ. Определяем существенные переменные функции f и рассматриваем две возможные линейные функции : сумма найденных существенных переменных и сумма существенных переменных плюс 1. Если исходная функция совпадает с одной из данных двух, то функция линейна. В противном случае функция нелинейная.
Корректность
данного метода следует из факта, что у
линейной функции![]()
![]() все переменные
все переменные![]() существенные и других существенных
нет.
существенные и других существенных
нет.
1) x1 существенная (по 1-ому и 5- ому) ,x2 существенная (по 3- ему и по 1-ому набору), x3 не существенная . Если функция линейная, то она имеет вид либо x1+x2, либо x1+x2+1; подходит первое выражение, поэтому первая функция линейная.
-
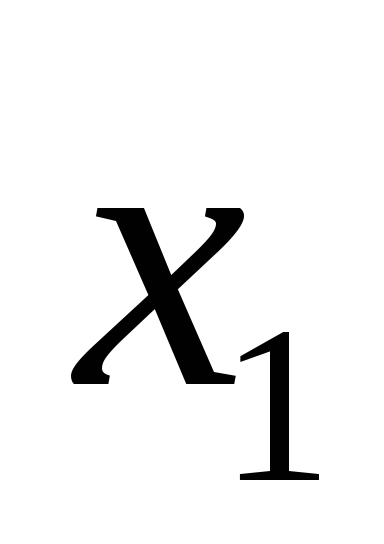
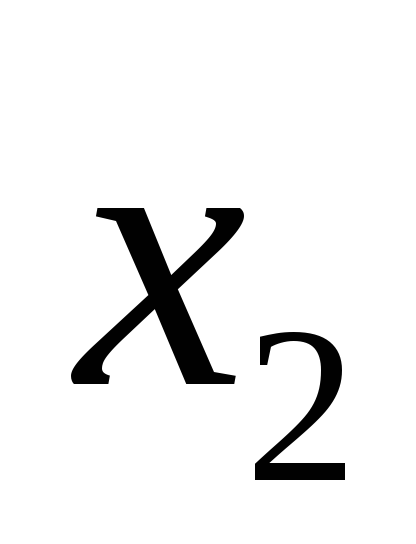
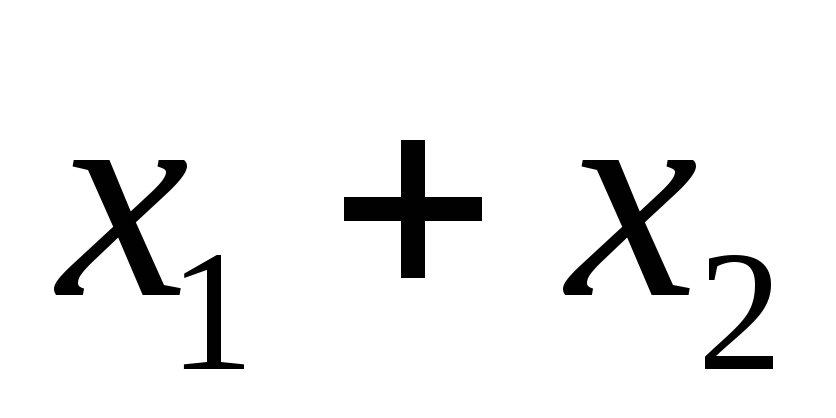
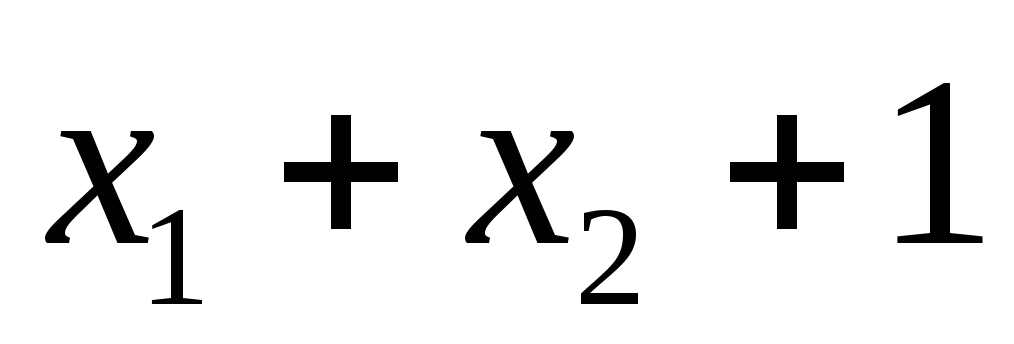
0
0
0
1
0
1
1
0
1
0
1
0
1
1
0
1
вторая функция нелинейная
2) x1 существенная (по 4-ому и 8-ому),x2 существенная (по 6-ому и 8-ому), x3 не существенная :
-
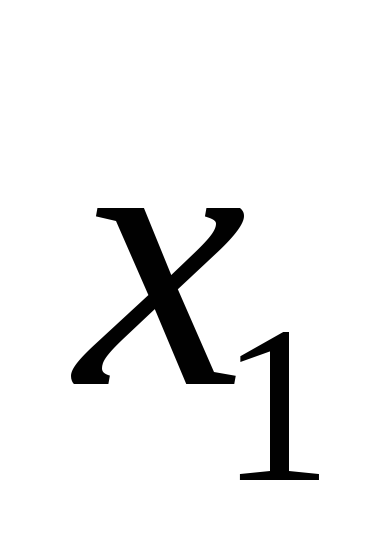
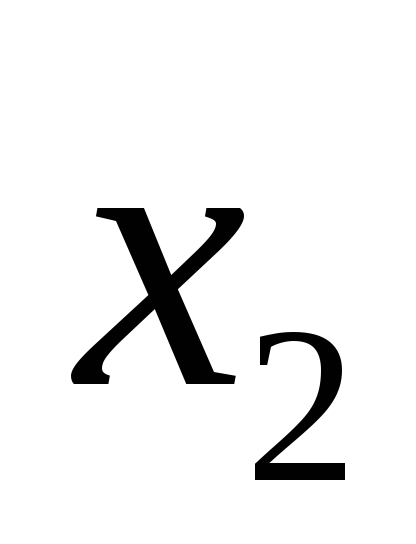
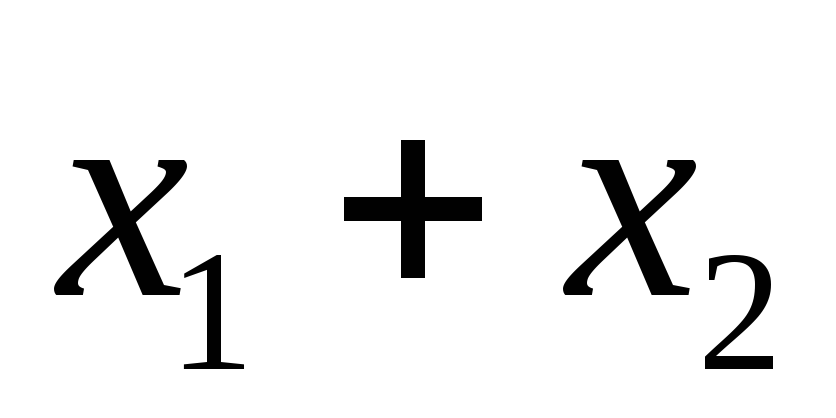
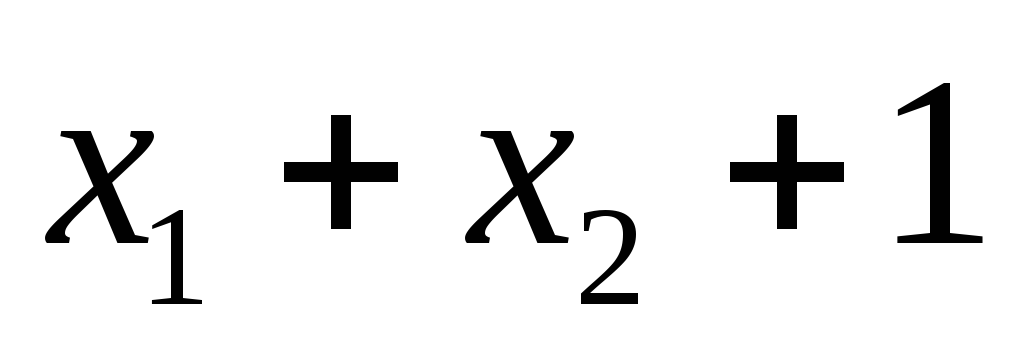
0
0
0
1
0
0
1
1
0
0
1
0
1
0
0
1
1
0
1
1
вторая функция нелинейная
Утверждение: все перечисленные пять классов являются замкнутыми, то есть суперпозиция любых двух функций из каждого класса является функцией тогоже класса.
Доказательство :
1) T0
Рассмотрим
![]() T0
T0
![]() T0
T0
Рассмотрим суперпозицию
![]() и покажем,
что полученная
и покажем,
что полученная
![]() T0.
Для этого найдем значение
T0.
Для этого найдем значение
![]() на нулевом наборе :
на нулевом наборе :
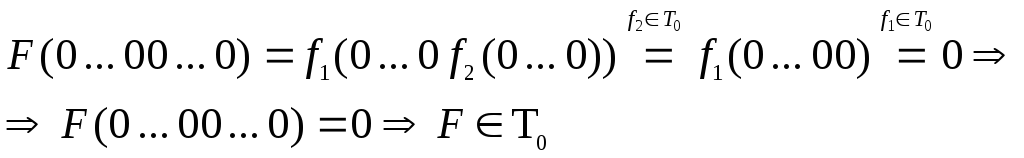
2) T1
Рассмотрим
![]() T1
T1
![]() T1
T1
Рассмотрим
![]() :
:
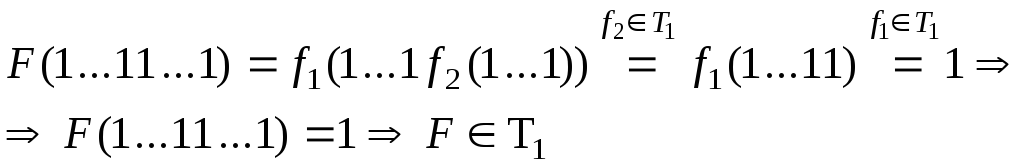
3) S
Рассмотрим
![]() S
S
![]() S
S
Рассмотрим
![]() :
:
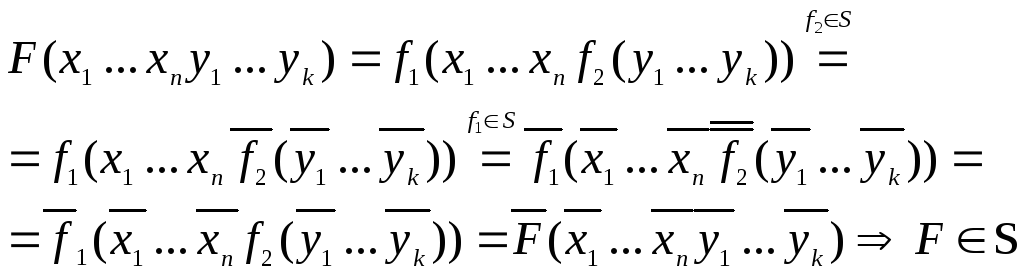
4) М
Рассмотрим
![]() М
М
![]() М
М
Рассмотрим суперпозицию
![]() :
и
:
и
рассмотрим
произвольную пару сравнимых наборов
![]() и
и![]() :
:![]() и покажем, что выполнено :
и покажем, что выполнено :![]() .
.
Нетрудно
видеть, что из того, что
![]() следует, что
следует, что![]() и
и![]() .
.
В силу того, что :
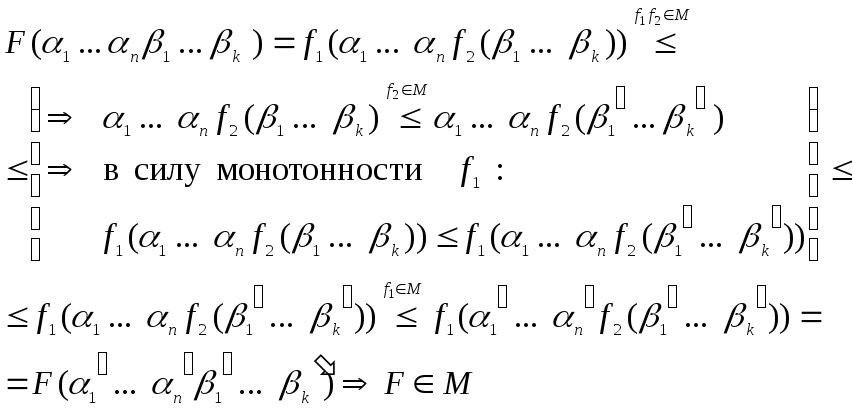
5) L
Рассмотрим
![]() L
L
![]() L
L
![]() , где
α и β
некоторые константы.
, где
α и β
некоторые константы.
Рассмотрим
![]() .
.
![]() .
.
Используя ассоциативность и коммутативность операции , преобразуем к виду :
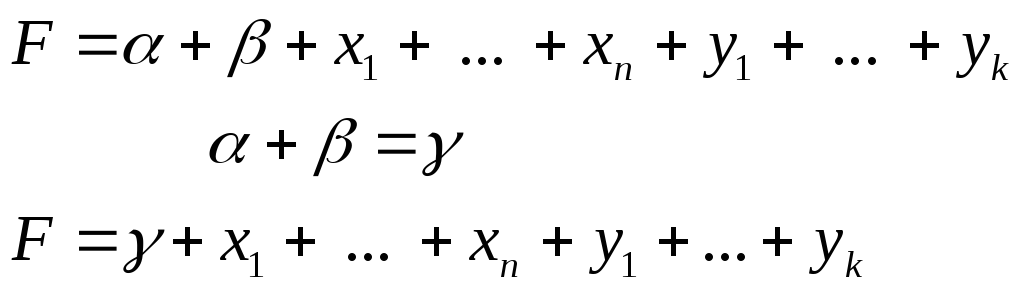 .
.
Степень
![]() не превосходит 1, следовательно
не превосходит 1, следовательно![]() L.
L.
Замечание Приведенные выше рассуждения будут справедливы, если множества переменных подставляемых функций пересекаются.
Упражнение Покажите, что переименование переменных не выводит функции из классов
![]() .
.
Критерий Поста полноты :
Для
того, чтобы система
![]() была полной, необходимо и достаточно,
чтобы она целиком не содержалась ни в
одном из пяти классов:T0,
T1
,
S,
M,
L.
была полной, необходимо и достаточно,
чтобы она целиком не содержалась ни в
одном из пяти классов:T0,
T1
,
S,
M,
L.

 0
0
 0
0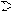 0
0 1
1