1. Основные понятия комбинаторики.

   1. Упорядоченные наборы а элементов n данных с возможными повторениями.

Пример. Упорядоченные наборы 3-х элементов множества {1,2} — это упорядоченные множества

{111} {112} {121} {122} {211} {212} {221} {222}. Упорядоченные наборы называют также словами.

Теорема. Число упорядоченных наборов с возможными повторениями а элементов из n данных есть n.

Доказательство. Пусть F есть искомое число упорядоченных набо­ров с повторениями элементов изn данных. Тогда разобьем все упорядоченные наборы на n групп, где в i-тую группу войдут те на­боры, которые начинаются на -ый элемент. В нашем примере, где n= 2 ,= 3 группы выглядят так:

1: 111, 112, 121, 122;

2: 211, 212, 221, 222.

Тогда число наборов в каждой группе равно числу

упорядоченных наборов -1 элементов изn данных, т. е. F, а число групп есть n. Поэтому

Пример 1. Дан алфавит из n букв . Найти число различных слов длины в этом алфавите.

Решение. Нетрудно видеть, что это число равно числу упорядоченных

наборов элементов из n данных, т. е .

Пример 2. Дано множество из n элементов . Найти число различных подмножеств этого множества.

Решение. Для каждого подмножества введем характери­стический вектор длины n, компонента i которого равна 1, если входит в рассматриваемое подмножество, и 0 в про­тивном случае. Тогда характеристический вектор (слово в {0,1} длиныn) однозначно определяет подмножество множества . Поэтому число подмножеств равно .

Пример 3. Пусть дано V — множество и множество Р некоторых упорядоченных пар . Тогда (V,P) называют ориентированным графом, V — множество вершин, Р — ориентированные ребра. Ребро называютпетлей. Полным ориентированным графом с петлями на множе­стве V называют граф со всеми ориентированными ребрами. Тогда число ребер в полном ориентированном графе равно .

1 1.2 Упорядоченные наборы элементов изn-данных

без повторения ().

Пример. , = 2. Тогда упорядоченные наборы без повторения:

.

Теорема. Число упорядоченных наборов элементов из n данных есть

где естьпроизведение.. Обозначают это число.

Доказательство. Пусть есть искомое число упорядоченных наборовэлементов изn данных без повторения. Тогда разобьем все эти наборы на n групп, в i-тую группу войдут наборы, начинающиеся на. Тогда число элементов вi-ой группе равно числу упорядоченных наборов - ого элемента из(— 1)-ого данного, так как элементы в наборе не повторяются, т.е. числу . Поэтому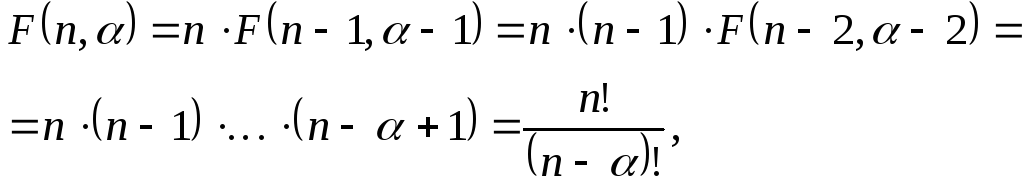

т.к.

В нашем примере группы выглядят так:

Упорядоченный набор n элементов из n данных без повторения называют перестановкой: 1,2,3. Перестановки

{123} {132} {213} {231} {312} {321} .

Число перестановок из n- элементов есть (0! считаем равным 1).

Пример 1. Пусть (V, Р) — ориентированный граф. Полным

ориентированным графом называют граф, в котором присутствуют все

ориентиро­ванные ребра, кроме петель.

Тогда ориентированные ребра такого графа есть упорядоченные

пары из множества без повторений, и их число по доказанной теореме есть

Пример 2. Имеется n мест и человек. Скольким числом способов можно рассадить этих человек наместах.

Решение. 1. . Занумеруем места числами 1,2, ... ,. Тогда каждому упорядоченному наборуэлементов изсоответствует способ посадки. Поэтому искомое число есть

.

2. Занумеруем людей 1,2,.. ,.. Тогда каждому упорядо­ченному выбору элементов изданных соответствует способ посадки и наоборот. Поэтому искомое число есть