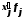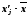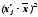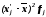ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«Государственный университет министерства финансов российской федерации»

Контрольная работа

по дисциплине

СТАТИСТИКА

Выполнил:

Студент(ка) 3 курса

группа № 2ЭО1/з

Бритикова Н. Н.

преподаватель:

научная степень,должность

Берлин Ю. И.

Оценка:_______

Дата «__»___________г.

Санкт-Петербург

2012

ВАРИАНТ 2

Имеются выборочные данные за год по регионам РФ (механическая выборка из 89 регионов), млн. руб.

Таблица 1 – Исходные данные

№ региона п/п	Среднегодовая стоимость основных фондов в промышленности (по полной балансовой стоимости)	Объем промышленной продукции
1	108200	208886
2	133950	222909
3	145554	276539
4	103139	155966
5	148026	295722
6	101503	150701
7	108197	208845
8	180707	325881
9	128373	209793
10	91700	104130
11	134805	221900
12	149647	219537
13	94550	144581
14	56700	93634
15	175833	256851
16	85716	119745
17	133379	343629
18	109424	169596
19	82364	148555
20	81889	142245
21	95617	119265
22	185442	409806
23	138102	276036
24	81366	142026
25	113170	175779
26	74695	74754
27	113415	192366
28	111642	123645
29	185445	345562
30	123940	161055

Задание 1

Признак – среднегодовая стоимость основных фондов промышленности (по полной балансовой стоимости). Число групп – пять.

Задание 2

Связь между признаками - среднегодовая стоимость основных фондов промышленности (по полной балансовой стоимости) и объем промышленной продукции

Задание 3

По интервальному вариационному ряду, построенному в задаче 1, с вероятностью 0,95 (t=1,96) вычислите для генеральной совокупности: а) среднюю стоимость основных фондов промышленности б) долю регионов со среднегодовой стоимостью основных фондов промышленности более 133947 млн. руб.

Задание 4

Имеются данные об остатках оборотных средств организации за I полугодие 2008 г. (тыс. руб.):

01.01.08 г.	120
01.02. 08 г.	130
01.03. 08 г.	135
01.04. 08 г.	132
01.05. 08 г.	139
01.06. 08 г.	143
01.07. 08 г.	127

Определите:

1. средний остаток оборотных средств за I и II кварталы, за I полугодие 2008 г.;

2. абсолютный и относительный прирост среднего остатка оборотных средств во II-ом квартале по сравнению с I-ым.

Задание 1.

где –наибольшее и наименьшее значения признака в исследуемой совокупности,k - число групп интервального ряда.

h = (185445– 56700) / 5 =25749 руб.

Границы интервалов

Номер группы	Нижняя граница, чел.	Верхняя граница, чел.
1	56700	82449
2	82449	108198
3	108198	133947
4	133947	159696
5	159696	185445

Определяем число границ, входящих в каждую группу, используя принцип «исключительно», согласно которому фирмы с граничными значениями признаков, будем исключать из первого интервала, где впервые встречается это значение, и относить к следующему интервалу.

Разработочная таблица для построения интервального ряда распределения и аналитической группировки

Группы фирм по среднесписочной численности менеджеров, чел.	Номер	Среднесписочная численность менеджеров, чел.	Объем продаж, млн. руб.
1	2	3	4
56700 - 82449	14	56700	93634
	26	74695	74754
	24	81366	142026
	20	81889	142245
	19	82364	148555
Всего	5	377014	601214
82449-108198	16	85716	119745
	10	91700	104130
	13	94550	1445581
	21	95617	119265
	6	101503	150701
	4	103139	155966
	7	108197	208845
Всего	7	680422	1003233
108198-133937	1	108200	208885
	18	109424	169596
	28	111642	123645
	25	113170	175779
	27	113415	192366
	30	123940	161055
	17	133379	343629
	9	128373	209793
Всего	8	941543	1584748
133937- 159686	2	133950	222909
	11	134805	221900
	23	138102	276036
	3	145554	276539
	5	148026	295722
	12	149647	219537
Всего	6	850084	1512643
159686- 188435	15	175833	255685
	8	180707	325881
	29	185445	409806
	22	185442	409806
Всего	4	1083967	1336934

Итого 30 3933030 6038772

Таблица 4 - Распределение фирм по среднегодовой стоимости основных фондов.

Номер группы	среднегодовая ст-ть основных фондов в промышленности руб.	Число фирм
1	56700-82449	5
2	82449 - 108198	7
3	108198 -133947	8
4	133947-159696	6
5	159696 - 185445	4
	ИТОГО	30

Приведем еще три характеристики полученного ряда распределения - частоты групп в относительном выражении, накопленные (кумулятивные) частоты Sj, получаемые путем последовательного суммирования частот всех предшествующих (j-1) интервалов, и накопленные частости, рассчитываемые по формуле .

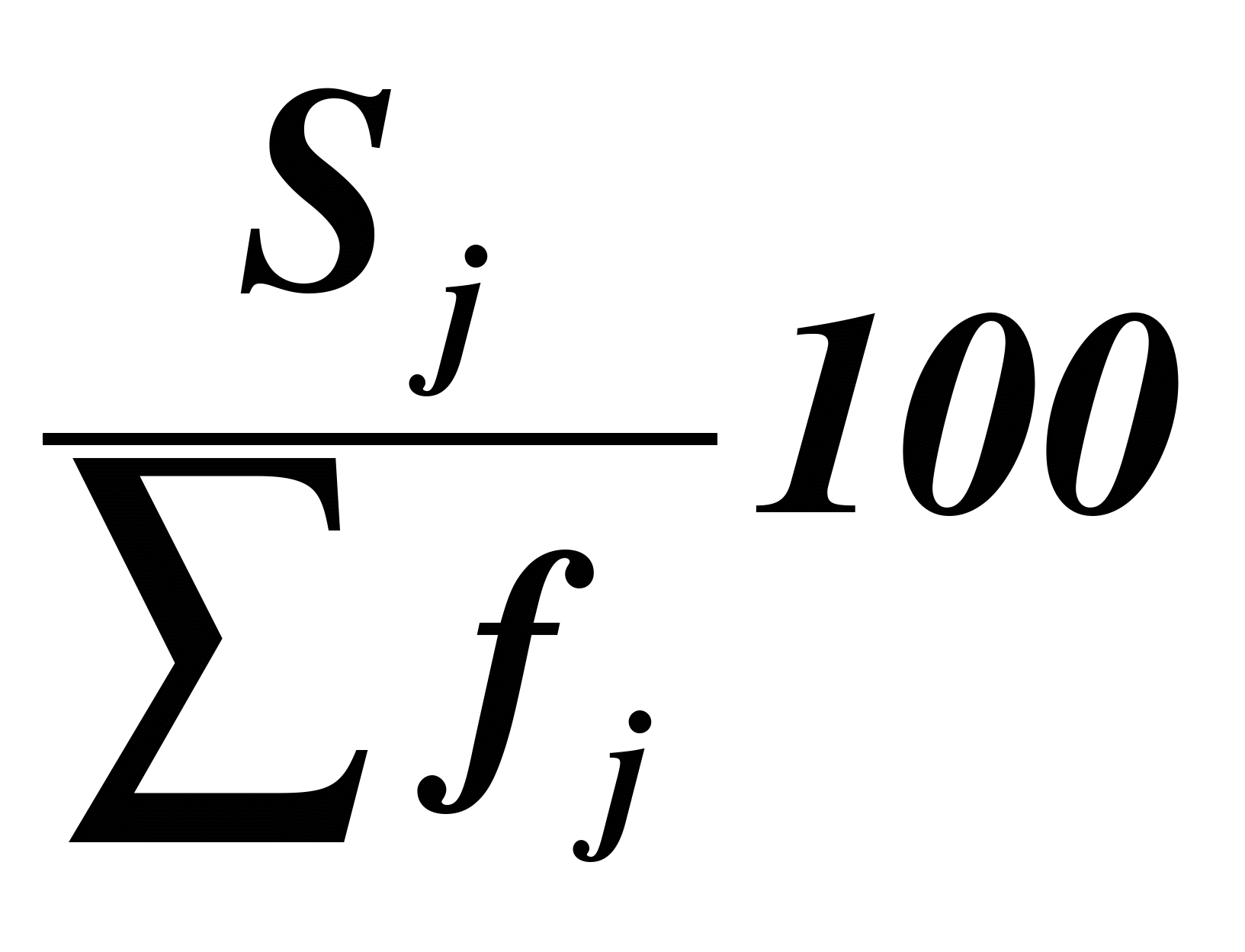Таблица 5 - Структура фирм по среднесписочной численности менеджеров

Номер группы	Группы фирм по среднегодовой ст - ти основных фондов x	Число фирм, f		Накопленная частота Sj	Накопленная частость, %
		в абсолютном выражении	в % к итогу
1	2	3	4	5	6
1	56700 -82449	5	17,7	5	17
2	82449 -108198	7	23,3	12	40
3	108198 - 133947	8	27,7	20	67
4	133947 - 159696	6	20	26	87
5	159696 - 185445	4	13	30	100
	ИТОГО	30	100	93

Вывод : Распределение не равномерное.

3. Нахождение моды и медианы полученного интервального ряда распределения графическим методом и путем расчетов

Для определения моды графическим методом строим по данным табл. 4 (графы 2 и 3) гистограмму распределения фирм по изучаемому признаку.

8
7
6
5
4
0	56700	82449	108197	133947	159696	185445

Рисунок 1 - Определение моды графическим методом

Расчет конкретного значения моды для интервального ряда распределения производится по формуле:

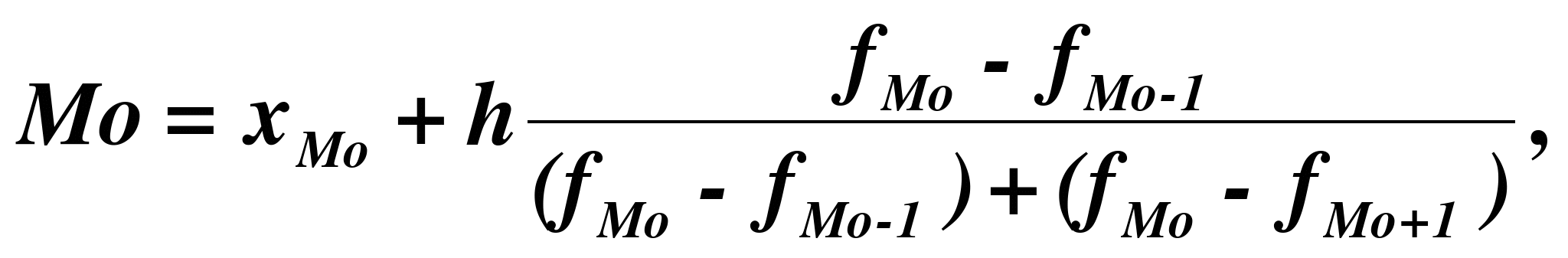
где х_Мo – нижняя граница модального интервала,

h – величина модального интервала,

f_Mo – частота модального интервала,

f_Mo-1 – частота интервала, предшествующего модальному,

f_Mo+1 – частота интервала, следующего за модальным.

Согласно табл. 4 модальным интервалом построенного ряда является интервал 35 - 40 чел., т.к. он имеет наибольшую частоту (f₄=10). Расчет моды:

108198*25749(8-7/(8-7)(8-6))=116695р

Вывод. Для рассматриваемой совокупности фирм наиболее распространенная среднегодовая стоимость основных фондов характеризуется средней величиной 116695 рублей

Для определения медианы графическим методом строим по данным табл. 5 (графы 2 и 5) кумуляту распределения фирм по изучаемому признаку.

Рисунок 2 - Определение медианы графическим методом

Расчет конкретного значения медианы для интервального ряда распределения производится по формуле

,

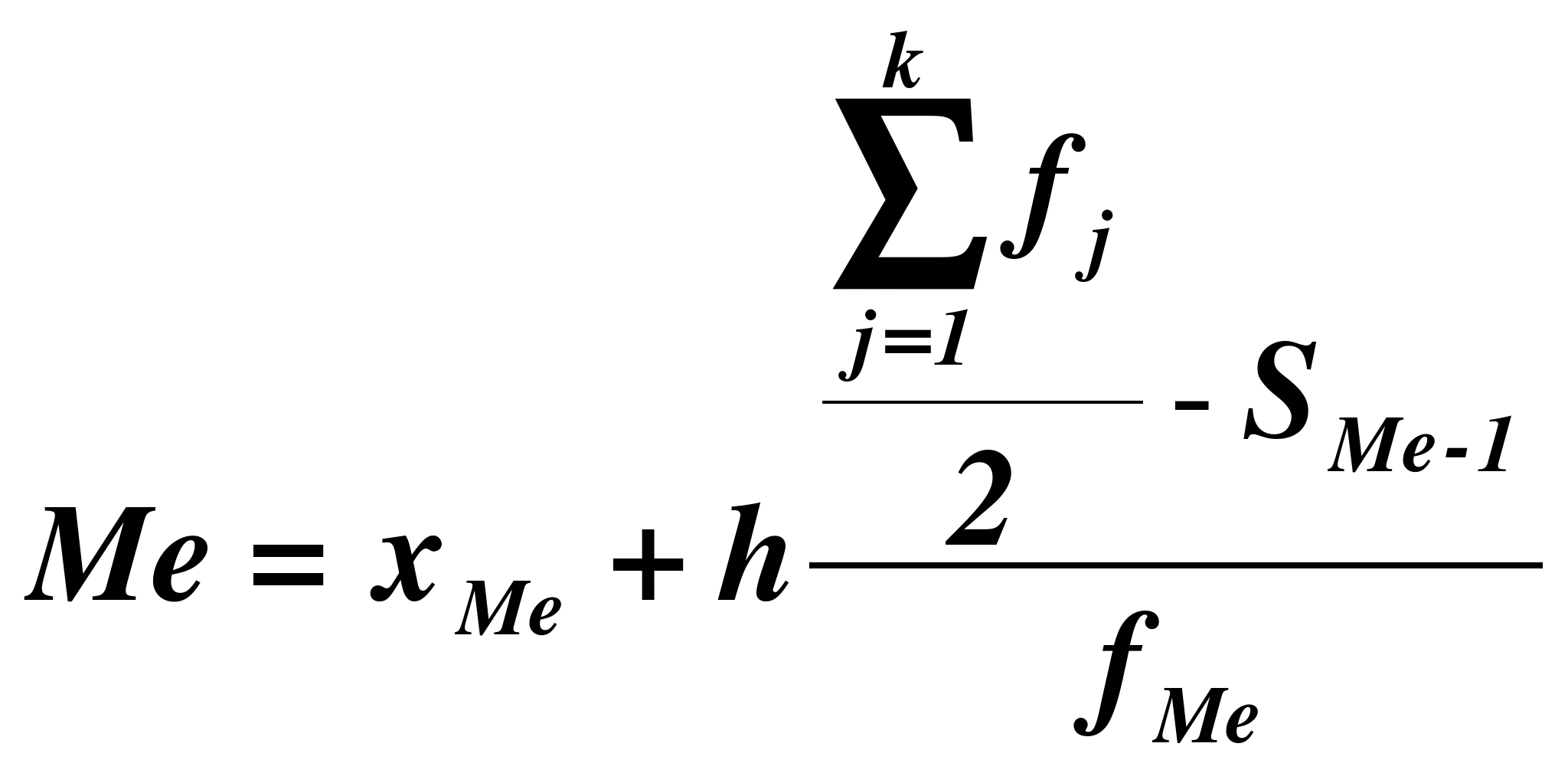где х_Ме– нижняя граница медианного интервала,

h – величина медианного интервала,

–сумма всех частот,

f_Ме – частота медианного интервала,

S_Mе-1 – кумулятивная (накопленная) частота интервала, предшествующего медианному.

Определяем медианный интервал, используя графу 5 табл. 5. Медианным интервалом является интервал 35-40 чел., т.к. именно в этом интервале накопленная частота S_j=23 впервые превышает полусумму всех частот ().

Ме = 108198*25749((15-12)/8 = 118498руб.

Вывод. В рассматриваемой совокупности половина фондов промышленности имеют среднегодовую стоимость основных фондов не более 118496 руб., а другая половина – не менее 118498 руб..

Расчетная таблица для нахождения характеристик ряда распределения

Для расчета характеристик ряда распределения ,σ, σ², V_σ на основе табл. 5 строим вспомогательную таблицу 6 ( – середина интервала).

среднегодоая ст-сти основн фондов	Середина интервала (среднее число основных фондов промышл.),	Число фирм, fj	Общее число основных фондов
1	2	3	4	5	6	7
56700 - 82449	69574,5	5	347842,50	-48923,10	2393469713	11967348568
82449-108198	95323,5	7	667264,50	-23174,10	537038910	3759272376
108198-133937	121073	8	968580,00	2574,90	6630110,01	53040880,08
133937- 159686	146821,5	6	880929,00	28323,90	802243311	4813459868
159686- 188435	172570,5	4	690282,00	54072,90	2923878514	11695514058
ИТОГО	172570,50	30	3554898	-	2393469713,00	32288635749

X= (3554898/30=118496,6) 3933030 / 30 = 131101

Рассчитаем среднюю арифметическую взвешенную:

Х =1076227858,3=3280,6

Рассчитаем дисперсию:

32288635749/30= 1076287858,3

Рассчитаем коэффициент вариации:

V=6/118496,6=0,005%

Величина V оценивает интенсивность колебаний вариантов относительно их средней величины. Принята следующая оценочная шкала колеблемости признака:

0%<V40%- колеблемость незначительная;

40%< V60%- колеблемость средняя (умеренная);

V>60% - колеблемость значительная.

Вывод. Анализ полученных значений показателей 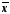иσ говорит о том, что средняя величина среднегодовой стоимости основных фондов составляет 118496,6 руб.

Значение V = 0,005% Расхождение между значениями 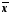,Мо и Ме незначительно, что подтверждает вывод об однородности совокупности фондов.