Вариант 6

1. Даны матрицы

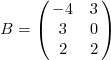и . Найдите матрицы С=А∙В, С=A+B, C=A-B.

2. Решите систему уравнений методом Крамера и методом Гаусса

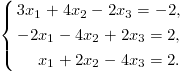
3. Выпишите общее решение системы уравнений

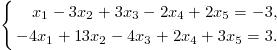
Для этого найдите базисное решение х* и нормальную фундаментальную систему решений соответствующей однородной системы.

4. Найти все собственные векторы линейного преобразования А, если в некотором базисе векторного пространства матрица линейного преобразования равна

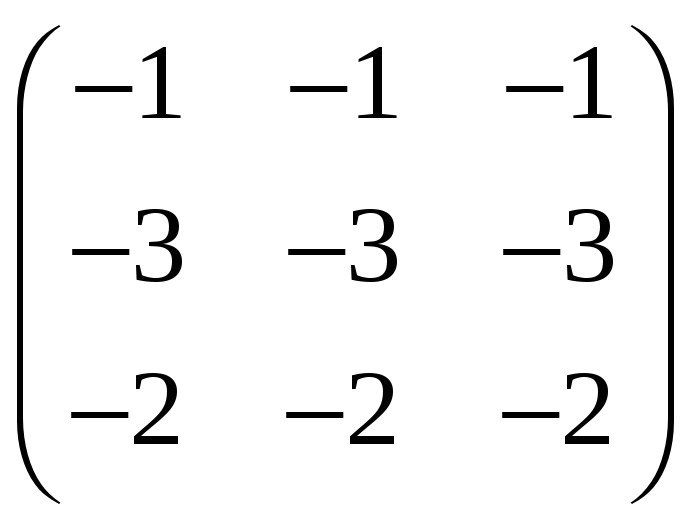
5. Привести квадратичную форму к каноническому виду методом Лагранжа.

6. Пусть вектор принадлежит векторному пространству L и в некотором базисе этого пространства имеет следующие координаты: 2, 3 и 5. В L введен новый базис Найти координаты вектора в новом базисе.

7. Графическим методом решить задачу линейного программирования.

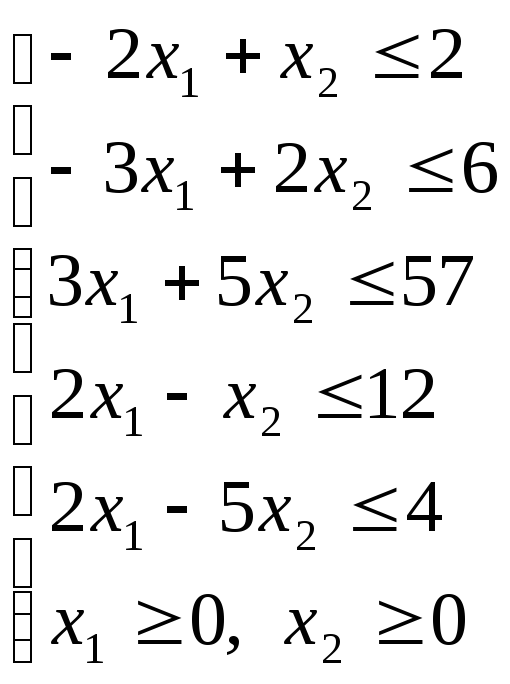
8. Решите транспортную задачу.

	60	50	60	50
70	2	9	7	5
40	3	9	6	3
80	5	1	3	8
50	6	8	9	9

F_min=

9. Решить прямую и двойственную задачи линейного программирования.

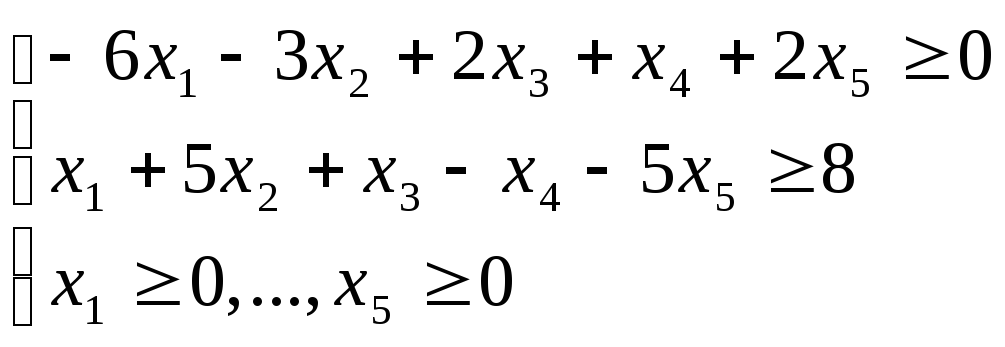
10. Решить задачу линейного программирования симплекс-методом.

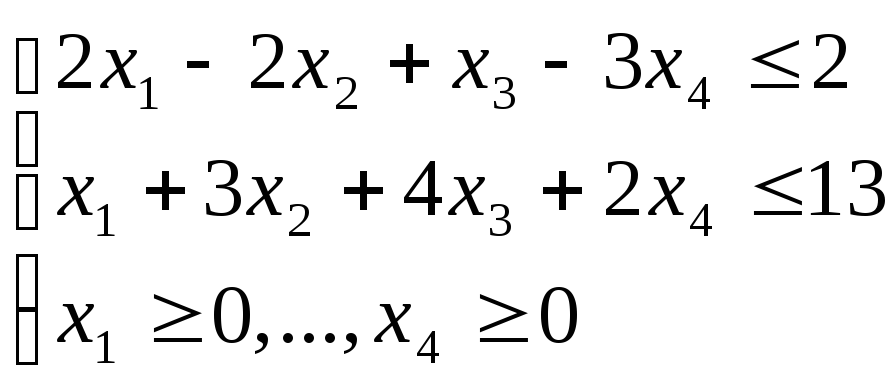
Вариант 7

1. Даны матрицы

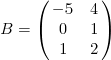и . Найдите матрицы С=А∙В, С=A+B, C=A-B.

2. Решите систему уравнений методом Крамера и методом Гаусса

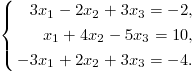
3. Выпишите общее решение системы уравнений

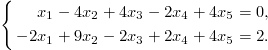
Для этого найдите базисное решение х* и нормальную фундаментальную систему решений соответствующей однородной системы.

4. Найти все собственные векторы линейного преобразования А, если в некотором базисе векторного пространства матрица линейного преобразования равна

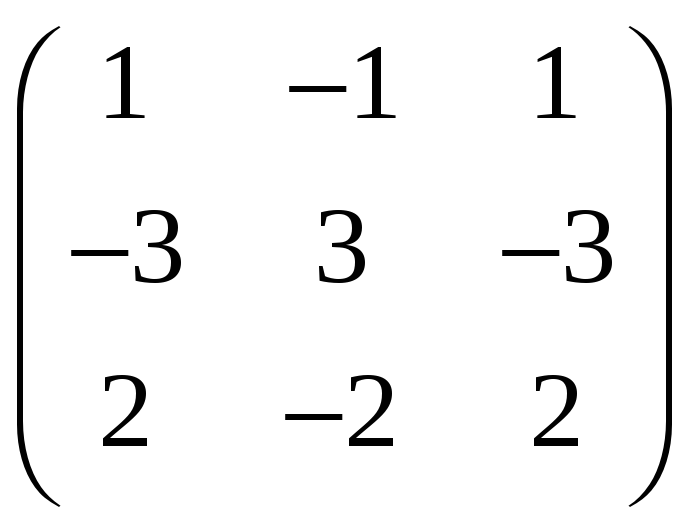
5. Привести квадратичную форму к каноническому виду методом Лагранжа.

6. Пусть вектор принадлежит векторному пространству L и в некотором базисе этого пространства имеет следующие координаты: 5, 1 и 1. В L введен новый базис Найти координаты вектора в новом базисе.

7. Графическим методом решить задачу линейного программирования.

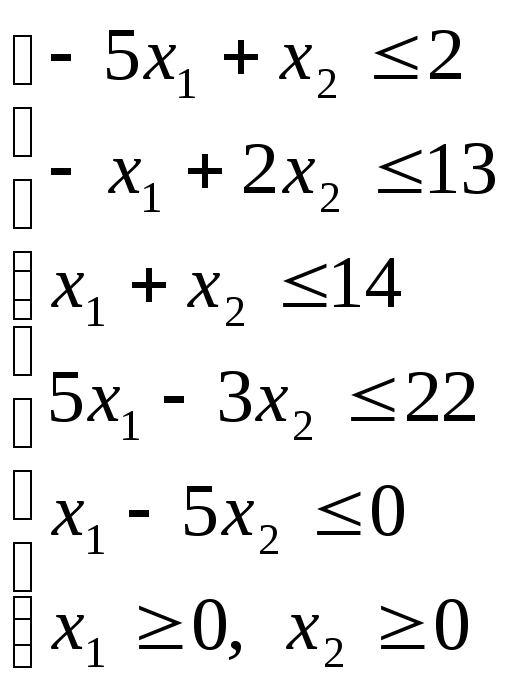
8. Решите транспортную задачу.

	80	100	140	100
100	5	5	3	3
100	7	3	7	4
100	5	5	5	6
100	6	3	4	5

F_min=

9. Решить прямую и двойственную задачи линейного программирования.

10. Решить задачу линейного программирования симплекс-методом.