
- •Линии передач.
- •Волновое сопротивление.
- •Телеграфное уравнение в гиперболической форме.
- •Телеграфное уравнение для идеальной линии. Входное сопротивление.
- •Режимы работы линии передачи.
- •Работа линии в режиме бегущих волн.
- •Работа линии в режиме стоячих волн, линия разомкнута на конце.
- •Работа линии в режиме стоячих волн. Короткозамкнутая линия.
- •Металлические изоляторы.
- •Работа линии в режиме смешанных волн
- •Согласование сопротивлений в линии передачи.
- •Общие сведения о волнах в прямоугольном волноводе.
- •Распределение полей в прямоугольном волноводе.
- •Антенны.
- •Излучение антенны типа диполь (линейный симметричный вибратор, лсв).
- •Диаграмма направленности антенны типа диполь.
- •Сопротивление излучения антенны типа диполь.
- •Апертурные (поверхностные) антенны.
- •Рупорная антенна.
- •Параболические антенны.
Режимы работы линии передачи.
В зависимости от сопротивления нагрузки меняется распределение напряжения, тока и входного сопротивления, что определяет режим работы л.п.
Л.п. может работать в режимах бегущих, стоячих и смешанных волн.
Рис.8.

Пусть Xбудет соответствовать
любой реактивности, тогда сопротивление
нагрузки можно представить .
.
Рассмотрим частные случаи.
I. Пусть ,
тогда
,
тогда .
.
1.1.
 - режим бегущих волн
- режим бегущих волн
1.2.
 - режим смешанных волн
- режим смешанных волн
II. Пусть (режим
к.з.) - режим стоячей волны в линии.
(режим
к.з.) - режим стоячей волны в линии.
III. Пусть (обрыв линии) - режим стоячей волны в
линии.
(обрыв линии) - режим стоячей волны в
линии.
IV. Пусть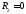 ,
тогда
,
тогда -
режим стоячей волны.
-
режим стоячей волны.
В общем случае, если
 ,
и все величины отличны от 0, получаем
режим смешанных волн.
,
и все величины отличны от 0, получаем
режим смешанных волн.
Рис.9.
Работа линии в режиме бегущих волн.
Рис.10.
Режим бегущих волн будет обеспечен в
случае, если
 .
Пусть в начальный момент времени
генератор отправляет в линию падающие
волны напряжения и тока. По закону Ома
для любого произвольного сечения будет
выполнятся:
.
Пусть в начальный момент времени
генератор отправляет в линию падающие
волны напряжения и тока. По закону Ома
для любого произвольного сечения будет
выполнятся: ,
следовательно в сечении нагрузкиx= 0, ток будет иметь вид
,
следовательно в сечении нагрузкиx= 0, ток будет иметь вид .
.
В результате около нагрузки разности напряжений или токов не возникает, по закону электромагнитной индукции отраженной волны не появляется, то есть вся энергия, отдаваемая генератором в линию, поглощается нагрузкой.
Рассмотрим телеграфное уравнение для данного режима.
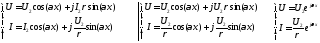
Процесс является гармоническим во
времени. Следовательно, существует
амплитудное значение, которое соответствует
максимальному гармоническому колебанию
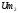 .
ТогдаU2можно
представить в виде:
.
ТогдаU2можно
представить в виде: .
.
Тогда система телеграфных уравнений
может быть представлена в виде:
 .
.
Отсюда можно посчитать мгновенное
значение:
 .
.
Выводы:1. Напряжение и ток в лини синфазны, следовательно, характер сопротивления чисто активный.
2. Пространство (координата х) и время
(координата t) являются
аргументами одной и той же периодической
тригонометрической функции, что
характеризует распространяющуюся
бегущую волну. Так как -
волна распространяется без затухания.
-
волна распространяется без затухания.
3. Входные сопротивления не зависят от длинны линии и являются чисто активными. Следовательно, генератор работает с наибольшим КПД.
Работа линии в режиме стоячих волн, линия разомкнута на конце.
Рис.11.
Линия, разомкнутая на конце, эквивалентна
 .
Пусть в начальный момент времени от
генератора к нагрузке распространяется
падающие волны тока и напряжения. Для
произвольного х, причем
.
Пусть в начальный момент времени от
генератора к нагрузке распространяется
падающие волны тока и напряжения. Для
произвольного х, причем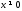 ,
по закону Ома можно записать:
,
по закону Ома можно записать: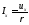 ,
то есть
,
то есть .
Однако, для сечения нагрузки можно
записать:
.
Однако, для сечения нагрузки можно
записать: ,
то есть около нагрузки происходит
уменьшение тока.
,
то есть около нагрузки происходит
уменьшение тока.
Как известно, в соответствии с законом электромагнитной индукции, уменьшающийся во времени или пространстве ток порождает ЭДС индукции (напряжение), которая в свою очередь порождает ток индукции. При этом токи будут противофазны, а по закону сохранения энергии их амплитуды будут равны.
В результате в л.п. уменьшение тока около нагрузки порождает отраженную волну тока той же амплитуды, но противоположной фазы. Так как частота не меняется в л.п. происходит интерференция волн, в результате которой образуется стоячая волна.
Для вывода телеграфных уравнений воспользуется системой телеграфных уравнений.

В л.п. существуют падающие и отраженные волны, следовательно, можно переписать падающие/отраженные волны в следующем виде:
Для падающей волны:

Для отраженной волны:
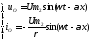
Отраженные волны распространяются в
направлении оси х, поэтому перед
 появляется
«-». Волна тока распространяется в
противофазе, поэтому для тока появляется
«-» для всей правой части.
появляется
«-». Волна тока распространяется в
противофазе, поэтому для тока появляется
«-» для всей правой части.
В результате интерференции:
 .
.
Выводы:1. Пространстваxиtявляются аргументами различных тригонометрических функций, следовательно, в линии образуются стоячие волны.
2. Распространение узлов и пучностей характеризуется выражением в [ ], а во времени { }.
3. Во времени напряжение и ток сдвинуты
по фазе на
 ,
это свидетельствует о реактивном
характере энергии в л.п.
,
это свидетельствует о реактивном
характере энергии в л.п.
4. Линия обладает резонансными свойствами, потому что амплитудное значение может быть больше исходного.
5. Рассчитаем входное сопротивление используя телеграфные уравнения для идеальной линии передачи.

Входное сопротивление чисто реактивно,
меняется от до
до ,
проходя через 0. Зависит от координатыx; периодически повторяется.
,
проходя через 0. Зависит от координатыx; периодически повторяется.
Рис.12.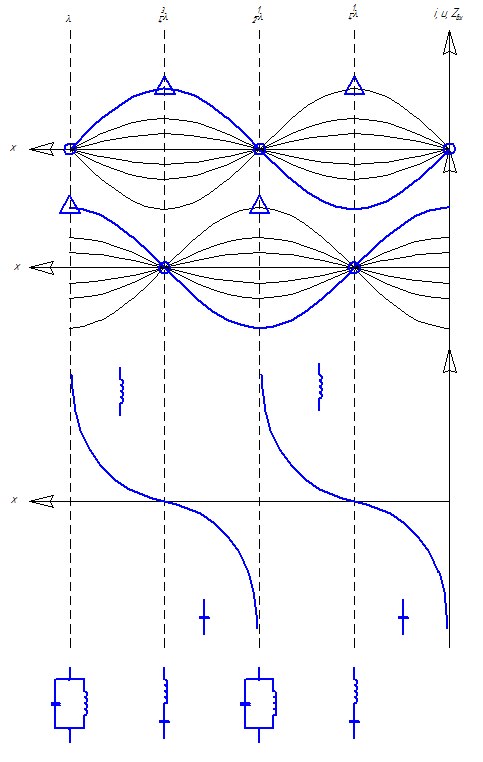

Выводы: 1. Через
каждые и
ток, и напряжения, и сопротивления
повторяются, следовательно, л.п. любой
длинны можно свести к линии передачи,
длинною не более полуволны.
и
ток, и напряжения, и сопротивления
повторяются, следовательно, л.п. любой
длинны можно свести к линии передачи,
длинною не более полуволны.
2. Узлы и пучности тока и напряжения отстоят друг от друга на четверть волны.
3. Отрезки линий, кратные
 ,
обладают резонансными свойствами, то
есть эквивалентны колебательным контурам
(последовательному или параллельному).
Подобные отрезки л.п. называютсяобъемными
резонаторами.
,
обладают резонансными свойствами, то
есть эквивалентны колебательным контурам
(последовательному или параллельному).
Подобные отрезки л.п. называютсяобъемными
резонаторами.
