4. Метод хорд

Геометрическая интерпретация метода хорд приведена на рис. 5.16. Проведем через точки (a, y_a) и (b, y_b) прямую. Уравнение этой прямой:

Рис. 5.16 Графическая иллюстрация

метода хорд

Начальное приближение корня равно абсциссе точки пересечения и оси абсцисс (легко определяется также из соответствующих пропорций):

Из двух отрезков [a, x₀] и [x₀, b] выберем тот, на концах которого функция f(x) имеет разные знаки (т. е. отрезок, содержащий корень уравнения). Проведем секущую на новом отрезке [x₀, b] и получим следующее приближение корня x₁. Формируем последовательность x₀, x₁, x₂, …, x_n, … до выполнения условия

|x_n – x_n-1| < ε.

Схема алгоритма уточнения корня методом хорд (методом пропорциональных частей) приведена на рис. 5.17.

4. Алгоритмы обработки массивов

   1. Определение минимального элемента в массиве.

Задача нахождения минимума (или максимума) в массиве из N элементов может быть решена последовательным сравнением "текущего" минимального (максимального) значения со значением очередного элемента массива и "запоминанием" при необходимости нового значения. Схема алгоритма показана на рис. 5.18.

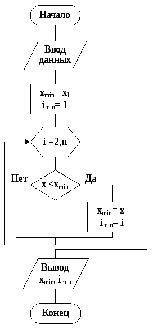
Рис. 5.18 Алгоритм определения минимального элемента массива

2. Сортировка массива.

Допустим, необходимо упорядочить массив из N элементов по возрастанию. Задача решается последовательным сравнением пар соседних элементов массива и при необходимости их перестановкой. Сравнение происходит при N-1 проходах по всему массиву. Схема алгоритма показана на рис. 5.19.

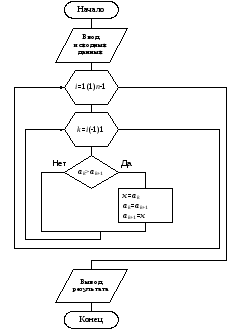
Рис. 5.19 Алгоритм сортировки массива методом пузырька

3. Произведение матриц

Пусть необходимо найти произведение двух матриц А и В размером 2х3 и 3х3 соответственно. Элементы результирующей матрицы С (размером 2х3) определяются по формуле

где n – число строк матрицы А;

m – число столбцов матрицы А и число строк матрицы В;

p – число столбцов матрицы В.

В общем случае результирующая матрица имеет размер np. Схема алгоритма умножения двух матриц представлена на рис. 5.20.

Рис. 5.20 Алгоритм умножения матриц

5. Алгоритм обработки строк

Пусть дана строка символов, группы символов в ней между одним или несколькими пробелами считаются словами. Подсчитать, сколько слов содержит строка, и вывести каждое из них на отдельной строке.

При решении задачи следует обратить внимание на следующую важную особенность. Если бы слово от слова отделялось только одним пробелом, то мы могли бы, посчитав количество пробелов, вычислить количество слов. В нашем случае необходимо перед каждым определением слова в строке удалять из нее первые пробелы и выделять слово до следующего пробела. После выделения слово удаляется из строки. Для выделения последнего слова строки, если в конце строки нет пробелов, за слово будет считаться оставшаяся часть строки.

Схема алгоритма решения данной задачи приведена на рис. 5.21. При этом алгоритм удаления пробелов в начале строки оформлен в виде процедуры, а выделения слова – в виде функции.

Рис. 5.21 Алгоритм подсчета количества слов в строке и их вывод