11.3 Задания и иные материалы, необходимые для оценки сформированности компетенций

Тесты

Вопрос 1

Под случайной величиной понимается величина:

- принимающая в результате эксперимента числовое значение, которое принципиально нельзя предсказать;

- принимающая в результате эксперимента числовое значение, которое можно точно предсказать;

- принимающая в результате эксперимента числовое значение, которое, при определенных условиях, нельзя точно предсказать.

Вопрос 2

В чем кроется причина изменения случайной величины в одном и том же эксперименте?

- в не учитываемых случайных факторах;

- в ошибках экспериментатора;

- в инструментальных ошибках.

Вопрос 3

Как правильно охарактеризовать случайную величину?

- заданием набора ее допустимых значений;

-заданием набора случайных значений;

- заданием конечного набора действительных значений.

Вопрос 4

Верно ли высказывание что «различают непрерывные и дискретные величины»?

- да;

- нет;

- может быть.

Вопрос 5

Верно ли высказывание, что «набор допустимых значений сам по себе слабо характеризует случайную величина. Для того, чтобы полностью охарактеризовать случайную величину, необходимо не только указать, какие значения она может принимать, но как часто?»

- можно;

- верно;

- затрудняюсь ответить.

Вопрос 6

В результате эксперимента дискретная случайная величина принимает конечное множество значений. Дайте математическое отражение частоты появления события. где-число опытов, в которых случайная величинаприняла значениек общему числу произведенных опытов:

• ;-;-; - .

Вопрос 7

Статическое определение вероятности события дискретной случайной величины называется такое событие математическая запись которого равна:

- ( при очень большом числе опытов)

- ( ( при очень большом числе опытов)

-( при очень большом числе опытов)

Вопрос 8

Чему равна вероятность достоверногособытия?

- 0,5;

- 1,0;

- 0,0;

- 10,0.

Вопрос 9

Чему равна вероятность невозможного события?

- 0,5;

- 1,0;

- 0,0;

- 10,0.

Вопрос 10

Чему равна сумма вероятностей всех возможных значений дискретной случайной величины ?

-

-

-

-

Вопрос 11

Можно ли дискретную случайную величину Х полностью задать вероятностным рядом, указав вероятность для каждого значенияв виде таблицы

			…….			…
			..……			…

• нельзя;

• можно;

• затрудняюсь ответить.

Вопрос 12

Всякое соотношение, устанавливающие связь между возможными значениями случайной величины и соответствующими им вероятностями, называется:

- законом соответствия;

- законом вероятности;

- законом распределения;

- законом регрессии.

Вопрос 13

Почему распределение непрерывной случайной величины нельзя задавать с помощью вероятностей отдельных значений?

- потому, что вероятность такого события может быть равно нулю по причине бесконечно большого числа их значений;

- потому, что вероятность такого события равна единице;

- не знаю.

Вопрос 14

Верно ли высказывание что «для непрерывных случайных величин изучается вероятность того, что в эксперименте значение случайной величины попадет в некоторую заранее намеченную совокупность чисел?»

- нет;

- затрудняюсь ответить;

- да;

- не знаю.

Вопрос 15

Известно, что вероятность, с которой случайная величина удовлетворяет некоторым неравенствам, обозначается ,где-случайная величина, а-произвольное действительное значение. Укажите правильную математическую запись вероятности события действительной случайной величины:

• 

• 

• 

Вопрос 16

При правильном ответе на предыдущий вопрос, укажите как называется вероятность события действительной случайной величины как функции от :

• законом вероятности;

• законом регрессии;

• законом соответствия;

• законом распределения.

Вопрос 17

Является ли функция неубывающей функцией?:

• нет;

• затрудняюсь ответить;

• да.

Вопрос 18

Что представляет собой ордината кривой функции , соответствующей точке?

Представляет собой вероятность того, что случайная величина при эксперименте окажется:

• ;

• ;

• ;

• ;

Вопрос 19

Дает ли разность двух ординат, соответствующая точкам вероятности события?:

• затрудняюсь ответить;

• да;

• нет.

Вопрос 20

На рис.1 графически представлена функция распределения дискретной

случайной величины, являющейся разрывной ступенчатой функцией. Скачки функции распределения происходят в точках (соответствующих возможным значениям дискретной случайной величины. Дайте ответ на вопрос чему равна сумма всех скачков? n; 6; 1; 0,5.

Рис. 1

Вопрос 21

Чему равны значения функции распределения непрерывной или дискретной случайной величины пи предельных значениях аргументаи?:

• 0 и 1;

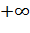• и;

• и;

• и.

Вопрос 22

Приведите математическую формулировку плотности распределения непрерывной случайной величины

• ;

• ;

• 

Вопрос 23

На рис. 2 графически представлена функция распределения непрерывной

случайной величины, являющейся непрерывной функцией . Определите значение вероятности того, что значения случайной непрерывной величины будут лежать в интервале между ; ; ; .

Рис. 2

Вопрос 24

Какой график представлен на рис. 3?

Рис.3

• функция распределения непрерывной случайной величины;

• функция плотности и распределения дискретной случайной величины;

• функция распределения непрерывной случайной величины;

• функция плотности распределения непрерывной случайной величины.

Вопрос 25

Почему плотность вероятности распределения случайной непрерывной величины

является важным её свойством ?:

• потому, что попадание непрерывной случайной величины в интервал есть достоверное событие;

• потому, что попадание непрерывной случайной величины в интервал есть невероятное событие;

• потому, что попадание непрерывной случайной величины в интервал есть маловероятное событие.

Вопрос 26

Верно ли высказывание, что “вместо полного определения случайной величины в виде законов распределения вероятностей в прикладных задачах ее часто определяют с помощью числовых характеристик ?”:

• да;

• нет;

• не знаю;

• затрудняюсь ответить.

Вопрос 27

Что выражают собой числовые характеристикислучайной величины ?:

• постоянные величины, называемыми константами не случайной величины;

• действительные числа, выражающие характерные особенности случайной величины, называемых моментами случайной величины;

• натуральные числа, выражающие характерные особенности случайной величины, называемые моментами случайной величины

Вопрос 28

Укажите формулу начального момента К-го порядка для дискретной случайной величины :

• ;

• ;

• ;

• 

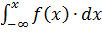Вопрос 29

Укажите математическую формулировку начального момента К-го порядка для непрерывной случайной величины :

• ;

• ;

• ;

• .

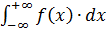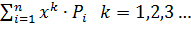Вопрос 30

Начальный момент какого порядка называетсяматематическим ожиданием (средним значением)непрерывнойслучайной величины?:

• ;

• ;

• ;

• .

Вопрос 31

Какие моменты случайной величины применяются чаще: начальные моменты дискретной и непрерывной или центральные моменты дискретной и непрерывной:

• начальные моменты непрерывной;

• начальные и центральные моменты дискретной величины;

• центральные моменты непрерывной и дискретной случайной величины;

• центральные моменты случайной величины.

Вопрос 32

Центральный момент дискретной случайной величины К-го порядка определяется по формуле Чему равен центральный момент первого порядка?:

• =1;

• =0;

• =10;

• =100.

Вопрос 33

Как называется второй центральный момент ?:

• математическое ожидание;

• дисперсия;

• коэффициент симметрии;

• коэффициент эксцесса.

Вопрос 34

Укажите математическую формулировку второго центрального момента для дискретной случайной величины:

• ;

• ;

• ;

• 

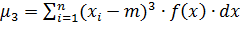Вопрос 35

Приведите альтернативные математические обозначения дисперсии:

• ;

• ;

• ;

• ;

• ;

• .

Вопрос 36

Корень квадратный из какого центрального момента называется средним квадратичным отклонением (стандартом) ?:

• ;

• ;

• .

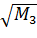Вопрос 37

Как называется третий центральный момент случайной величины, разделенный на ?:

• коэффициентом симметрии;

• коэффициентом эксцесса;

• коэффициентом асимметрии;

• коэффициентом регрессии.

Вопрос 38

Какие начальные моменты случайной величины входят в расчетную формулу третьего начального момента

• начальные моменты 1-го, 2-го и 3-го порядков;

• центральные моменты 1-го, 2-го и 3-го порядков;

• нулевые моменты 1-го, 2-го и 3-го порядков.

Вопрос 39

Четвертый центральный момент случайной величины вычисляется по формуле .

Укажите как вычисляются начальные моменты, входящие в формулу расчета четвертого центрального момента:

• …

• …

• …

• …

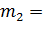Вопрос 40

Коэффициент эксцесса случайной величины определяется по формуле .

Укажите формулы для расчета четвертого центрального момента и

Вопрос 41

Назовите условие существования числовых характеристик-моментов случайной величины; ; ;

Моменты случайной величины существуют в том случае, если:

• соответствующие интегралы или ряды для дискретных величин сходятся;

• соответствующие интегралы или ряды для дискретных величин не сходятся;

• соответствующие интегралы или ряды для дискретных величин…

Вопрос 42

Можно ли построить нормированную случайную величину для случайной величины, если существует первый и второй моменты ?

- нет;

- затрудняюсь ответить;

- да.

Вопрос 43

Какие значения принимают математическое ожидание и дисперсиянормированной случайной величины ?

- ;

- ;

- ;

- .

Вопрос 44

Функция плотности распределения нормированной и ненормированнойслучайной величины связаны следующим выражением

где

Укажите какие параметры исвязывают случайные величиныи:

- (математическое ожидание; дисперсия);

- (начальный момент 2-го порядка; среднее квадратическое отклонение);

- (дисперсия; математическое ожидание).

Вопрос 45

Верно ли следующее выражение для функции распределения случайной ненормированной и нормированнойвеличины

- нет;

- да;

- затрудняюсь ответить.

Вопрос 46

Если моменты являются интегральными характеристиками распределения, то верно ли высказывание, что квантили характеризуют отдельные значения функции распределения или иначе , гдеквантиль функции распределенияслучайной величины?

- нет;

- да;

- затрудняюсь ответить.

- не знаю.

Вопрос 47

Известны значения двух квантилей . Верно ли следующее выражение, гдеи?

- нет;

- затрудняюсь ответить;

- не знаю;

-да.

Вопрос 48

Квантиль называется медианой распределения. Верно ли высказывание, что ордината медианы рассекает площадь между кривой плотности вероятности и осью абсцисс пополам (см. рис. 4) ?

Рис. 4

-нет;

-да;

-не знаю;

-затрудняюсь ответить.

Вопрос 49

Верно ли высказывание, что если распределение симметрично, то ?

- не знаю;

- нет;

- да;

- затрудняюсь ответить.

Вопрос 50

Как называется квантили и?

- аналогичными;

- симметричными;

- подобными.

11.4 Процедура оценивания знаний, умений, навыков

Оцениваемый показатель	Кол.баллов, обеспечивающих получение:
	Зачета
Процент набранных баллов из 100% возможных	от 60% и выше
Количество тестовых заданий:	Количество правильных ответов
15	8
20	11
25	13
30	16
40	22

Критерии оценки ответа студента

При определении оценки необходимо исходить из следующих критериев:

сумма знаний, которыми обладает студент (теоретический компонент – системность знаний, их полнота, достаточность, действенность знаний, прочность, глубина и др. критерии оценки);

понимание сущности явлений и процессов и их взаимозависимостей;

умение видеть основные проблемы (теоретические, практические), причины их возникновения;

умение теоретически обосновывать возможные пути решения существующих проблем (теории и практики).