Рассмотрим 2-й шаг.
|
Вклад |
Проект |
Остаток |
Прибыль из матрицы |
Прибыль за шаг |
|
Прибыль на шаге |
|
S1 |
Х2 |
S2 |
f (x2) |
F3 |
f+F |
F2 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
20 |
0 |
20 |
0 |
3 |
3 |
3 |
|
20 |
0 |
2 |
0 |
2 |
||
|
40 |
0 |
40 |
0 |
6 |
6 |
6 |
|
20 |
20 |
2 |
3 |
5 |
||
|
40 |
0 |
5 |
0 |
5 |
||
|
60 |
0 |
60 |
0 |
9 |
9 |
9 |
|
20 |
40 |
2 |
6 |
8 |
||
|
40 |
20 |
5 |
3 |
8 |
||
|
60 |
0 |
8 |
0 |
8 |
||
|
80 |
0 |
80 |
0 |
12 |
12 |
12 |
|
20 |
60 |
2 |
9 |
11 |
||
|
40 |
40 |
5 |
6 |
11 |
||
|
60 |
20 |
8 |
3 |
11 |
||
|
80 |
0 |
7 |
0 |
7 |
||
|
100 |
0 |
100 |
0 |
15 |
15 |
15 |
|
20 |
80 |
2 |
12 |
14 |
||
|
40 |
60 |
5 |
9 |
14 |
||
|
60 |
40 |
8 |
6 |
14 |
||
|
80 |
20 |
7 |
3 |
10 |
||
|
100 |
0 |
15 |
0 |
15 |
Рассмотрим 1-й шаг.
|
Вклад |
Проект |
Остаток |
Прибыль из матрицы |
Прибыль за шаг |
|
Прибыль на шаге |
|
S0 |
Х2 |
S2 |
f (x2) |
F2 |
f+F |
F1 |
|
100 |
0 |
100 |
0 |
15 |
15 |
15 |
|
20 |
80 |
3 |
12 |
15 |
||
|
40 |
60 |
4 |
9 |
13 |
||
|
60 |
40 |
9 |
6 |
15 |
||
|
80 |
20 |
11 |
3 |
14 |
||
|
100 |
0 |
12 |
0 |
12 |
Анализ результатов:
Максимальная прибыль равна 15 д.ед. Расположить денежные средства между проектами можно несколькими способами:
1)1 проект – 0 д.ед., 2 проект – 0 д.ед., 3 проект – 60 д.ед., 4 проект – 40 д.ед.
2)1 проект – 0 д.ед., 2 проект – 100 д.ед., 3 проект – 0 д.ед., 4 проект – 0 д.ед.
3)1 проект – 20 д.ед., 2 проект – 0 д.ед., 3 проект – 60 д.ед., 4 проект – 20 д.ед.
4)1 проект – 60 д.ед., 2 проект – 0 д.ед., 3 проект – 20 д.ед., 4 проект – 20 д.ед.
5)1 проект – 60 д.ед., 2 проект – 0 д.ед., 3 проект – 0 д.ед., 4 проект – 40 д.ед.
-
Задача распределения средств на четыре года
Для
двух предприятий выделено 1400 единиц
денежных средств. Как распределить все
средства в течение 4 лет, чтобы доход
был наибольшим, если известно, что доход
от х
единиц, вложенных в первое предприятие
равен
,
а доход от у
единиц, вложенных в первое предприятие
равен
.
Остаток средств к концу года составляет
-
для первого предприятия,
-
для второго предприятия. Решить задачу
методом динамического программирования.
Решение
Процесс распределения средств разобъем
на 4 этапа – по соответствующим
годам.
Обозначим 
-
средства, которые распределяются на
к–ом шаге как сумма средств по
предприятиям.
Суммарный доход от обоих предприятий на к–ом шаге:
Остаток средств от обоих предприятий на к–ом шаге:
Обозначим
- максимальный доход, полученный от
распределения средств 
между двумя предприятиями с к-го
шага до конца рассматриваемого
периода.
Рекуррентные соотношения
Беллмана для этих функций
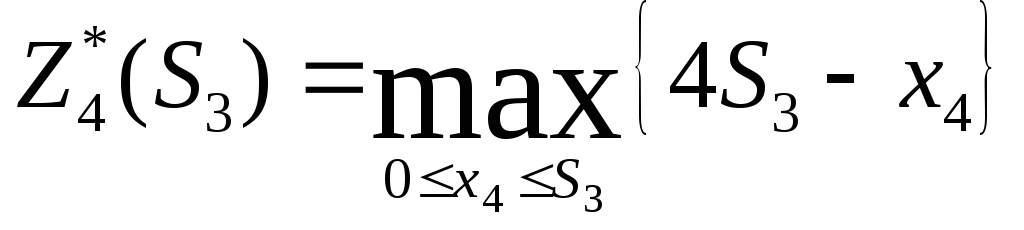
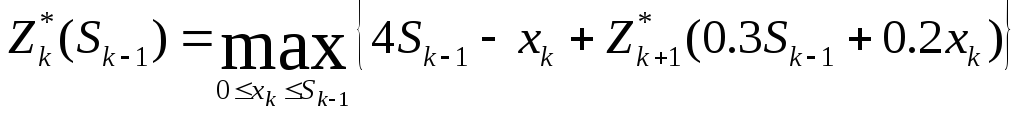
Проведем оптимизацию, начиная с четвертого шага:
4-й шаг.
Оптимальный доход
равен:
,
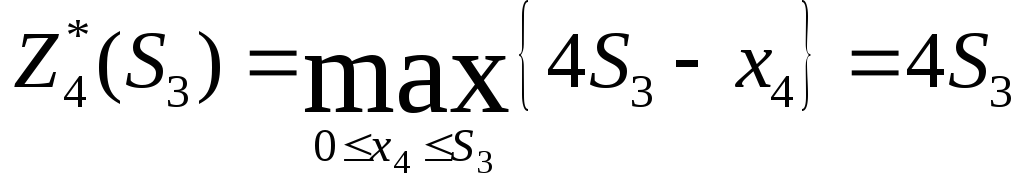т.к. линейная убывающая функция достигает
максимума в начале рассматриваемого
промежутка, т.е. при
3-й шаг.
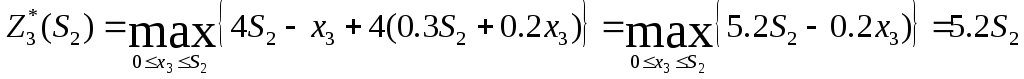
т.к. линейная убывающая функция
достигает максимума в начале
рассматриваемого промежутка, т.е. при
2-й шаг.
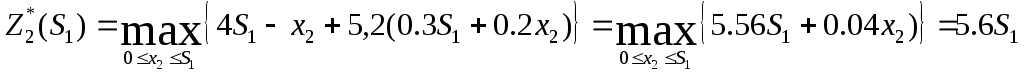
т.к. линейная возрастающая функция
достигает максимума в конце рассматриваемого
промежутка, т.е. при
.
1-й шаг.
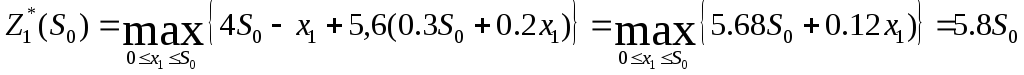
т.к. линейная возрастающая функция
достигает максимума в конце рассматриваемого
промежутка, т.е. при
.
Результаты оптимизации:
Определим количественное распределение средств по годам:
Т.к.
и
,
то
.
Получаем
Представим распределение средств в виде таблицы:
|
предприятие |
год |
|||
|
1 |
2 |
3 |
4 |
|
|
1 |
1400 |
700 |
0 |
0 |
|
2 |
0 |
0 |
350 |
105 |
При таком распределении средств за 4 года будет получен доход, равный
