mathematics_part_1_hamov

системы есть множество векторов параллельных (коллинеарных) между собой. Поэтому, если выбрать один ненулевой век-

тор (например, a a12 ; 1 ), то любой другой вектор, координаты

1 a11

a12 ≠ 0 (в противном случае система имеет нулевые коэффициенты). В этом случае y=0, x — свободная переменная и любая пара чисел (x,0), x — действительное число является решением системы. Таким образом, однородная система имеет ненулевые решения в том и только в том случае, когда ее определитель равен нулю.

Пример 5.1. Решить систему:

101

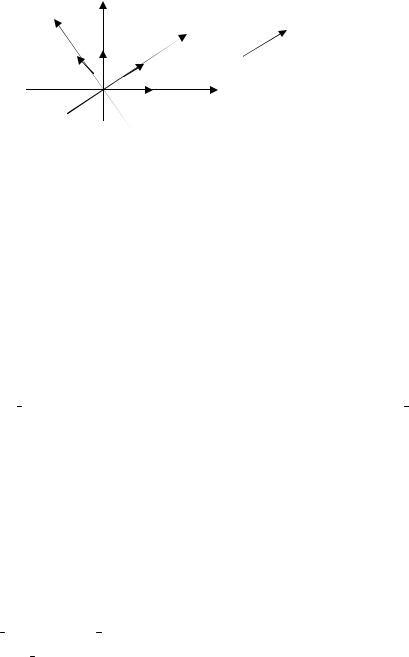
§ 2. Изменение координат вектора при изменении системы координат (поворот системы вокруг центра)

y

Рис. 5.1

Даны две прямоугольные системы координат (x 0 y) и (x′0 y′)

динаты вектора i ′, второй столбец – координаты вектора j′, называется матрицей перехода от системы координат (x 0 y) к системе (x′0 y′). Возьмем на плоскости произвольный вектор x , найдем его координаты (проекции на оси) в первой и во второй системах:

Записываем формулы (5.3) в матричном виде:

102

Таким образом, формулы (5.3), (5.4), (5.5) устанавливают зависимость между координатами одного и того же вектора x в двух различных системах координат (x 0 y) и (x′0 y′).

Пример 5.2. Новая система координат определена ортого-

Найти координаты вектора x {2; −3} в новой системе координат. Решение. Составляем матрицу перехода от системы коор-

динат, определяемой векторами i , j к системе, определяемой векторами i ′, j′.

Полученное матричное уравнение решаем одним из следующих двух способов:

1) Перемножаем матрицы, стоящие в правой части, а затем приравниваем соответствующие элементы матриц левой и правой частей. Получаем систему

2) Для матрицы T находим обратную матрицу T −1 , а далее находим X ′ по первой формуле (5.5):

103

Пример 5.3. Найти зависимость между координатами вектора в системах координат, если вторая система получена из первоначальной поворотом плоскости вокруг центра системы на угол α .

Рис. 5.2

Решение. Находим координаты векторов i ′, j′ в системе координат (xOy) (рис. 5.2)

i ′ = cosαi + cos (900 −α)j = cosαi +sin α j

j′ = cos (900 +α)i + cosα j = −sinαi + cosα j .

Матрица перехода от системы (x 0 y) к (x′0 y′) имеет вид:

Зависимость между координатами вектора x в первой и второй системах координат находится по формулам (5.5)

104

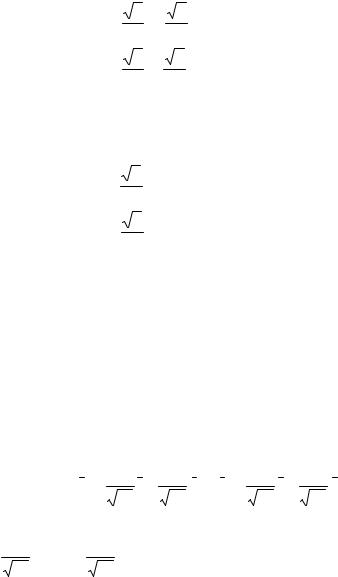
Пример 5.4. Преобразовать уравнение гиперболы x y =1 , используя формулы, полученные в предыдущем примере для случая, когда поворот плоскости осуществлен на угол α = 450.

Решение. При повороте на угол α = 450 матрица перехода от одной системы координат к другой имеет вид

Формулы преобразования координат точки (x; y) в (x′; y′):

Подставляя в уравнение x y =1 получим уравнение той же

Задания для самостоятельной работы

1. Новая система координат определена ортогональными

2. Новая система координат получена из первоначальной поворотом плоскости вокруг центра на угол 300. Найти матрицу переходаикоординаты вектора x{3; − 2} вновойсистеме координат.

105

задают линейное преобразование, переводящее точку плоскости с координатами (x1 , y1 ) (или вектор a1 {x1 ; y1 }) в точку с координатами (x2 ; y2 ) (или вектор a2 {x2 ; y2 }). Поэтому говорят, что задается отображение плоскости в себя. Перейдем к матричной записи системы (5.6), обозначая

Матрицу A называют матрицей линейного преобразования плоскости, которое определено формулами (5.6) или (5.7). Заметим, что любому линейному преобразованию, заданному формулами (5.6) соответствует единственная матрица A и обратно, любой матрице A соответствует единственное линейное преобразование вида (5.6) или (5.7).

Выясним, как изменяется матрица линейного преобразования, если от системы координат (x 0 y) перейти к новой системе (x′0 y′). . По формулам (5.5) получим:

106

матрица линейного преобразования в новой системе координат по формуле (5.10) имеет вид:

заданного в системе координат (x 0 y), в системе (x′0 y′) , опреде-

107

§ 4. Собственные числа, собственные векторы квадратной матрицы. Условия, при которых матрица подобна диагональной

число λ называют собственным значением (или собственным числом) матрицы A.

являются собственными векторами с собственными значениями соответственно λ1 = 5, λ2 =1, так как

108

X= x , что

y

AX = λX <=> AX −λX = 0 <=> AX −λEX = 0,

ственное значение тогда и только тогда, когда существует ненулевой вектор X , являющийся решением матричного уравнения

Матричное уравнение (5.12) равносильно однородной системе линейных уравнений:

Система (5.13) имеет ненулевые решения тогда и только тогда, когда ее определитель равен нулю:

Теорема доказана.

109

Определение 5.2. Уравнение (5.11) называют характеристическим уравнением матрицы A.

Из доказанной теоремы следует, что собственные числа матрицы A являются корнями характеристического уравнения (5.11). Для нахождения собственных чисел надо раскрыть определитель стоящий в левой части равенства (5.11), получим квадратное уравнение относительно λ , его корни — собственные числа A.

Для нахождения собственных векторов составляем однородную систему (5.13) для каждого из двух (или одного, если корни характеристического уравнения равны) собственных чисел. Ее решения – собственные векторы. Каждому собственному числу будет соответствовать бесконечное множество собственных векторов, но все они между собой имеют пропорциональные координаты. Матрица размера 2 ×2 может иметь не более двух собственных векторов с непропорциональными координатами. Если матрица A имеет два собственных вектора с непропорциональными координатами:

соответствующих собственным значениям λ1 , λ2 , то матрица A

венство:

причем столбцы матрицы T есть собственные векторы, соответ-

длины (орты). Тогда матрица T (см. 5.5) будет матрицей перехода от прямоугольной системы координат (x 0 y), определяемой векторами i , j к прямоугольной системе координат (x′0 y′), опре-

110