5.4. Множественный корреляционный анализ
В процессе осуществления строительства на результирующий показатель часто влияет не один, а несколько взаимозависимых факторов. Для учета их совокупного влияния необходимо использовать методы множественной корреляции.
Количественно
тесноту связи при множественной
корреляции можно оценить с помощью
множественного коэффициента корреляции
R.
Для этого необходимо определить парные
коэффициенты корреляции 
между
всеми факторами 
,
входящими в модель, результирующим
показателем y
и все парные коэффициенты корреляции
между факторами. Все коэффициенты
корреляции записываются в квадратную
симметричную матрицу:
Множественный коэффициент корреляции определяется по формуле:
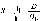
где D - определитель матрицы парных коэффициентов корреляции;
-
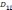
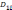определитель той же матрицы с вычеркнутыми
первой строкой и первым столбцом, т.е.
определитель матрицы парных коэффициентов
корреляции между факторами.
Для случая зависимости от двух факторов:
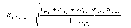
где р - истинный коэффициент корреляции.
Для определения влияния только одного i-ого фактора на результирующий показатель с исключением влияния других факторов используется частный коэффициент корреляции
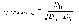
где
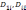
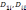соответственно
определители матрицы с вычеркнутой
первой строкой иi-м
столбцом и с вычеркнутой i-й
строкой и i-м
столбцом.
При множественной корреляции от двух факторов коэффициент частной корреляции первого фактора равен:
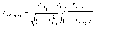
а коэффициент частной корреляции для второго фактора:
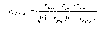
Частный
коэффициент корреляции отражает "чистое"
влияние фактора на результирующий
показатель и отличается от коэффициента
парной корреляции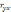 
.
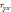При линейной форме связи множественный коэффициент корреляции является оценкой точности аппроксимации (определения) и равен корреляционному отношению; при нелинейных формах связи для оценки точности аппроксимации (оценки адекватности модели) применяются корреляционное отношение и ошибка аппроксимации, определяемые так же, как и при парной корреляции.
Существуют следующие формы зависимости при множественной корреляции - линейная, является частным случаем параболической зависимости; степенная и показательная, частным случаем последней является экспоненциальная зависимость. Методы определения многофакторных зависимостей излагаются в прикладной математике.
Вопросы для самопроверки
1. Пояснить смысл терминов:
- модель линейного программирования,
- целевая функция,
- оптимальное решение,
- система линейных уравнений.
2. Пояснить смысл терминов:
- максимизация и минимизация,
- множество допустимых решений,
- выпуклое множество,
- матрица,
- весовой коэффициент.
3. Объясните, как вы понимаете термины:
- транспортная задача,
- задача о назначениях.
4. Объясните, как вы понимаете следующие термины:
- сетевой график,
- критический путь,
- узел, вершина,
- дуга, ребро,
- путь.
5. Объясните, как вы понимаете следующие термины:
- динамическое программирование,
- принцип оптимальности,
- рекурсивное соотношение,
- оптимальная стратегия.
6. Объясните, как вы понимаете следующие термины с точки зрения теории управления запасами:
- рациональный объем поставок,
- рациональный объем складских помещений,
- длительность планового периода,
- выпуклая функция,
- вогнутая функция.
Задание на практическую работу
Составьте (опишите) пять задач, относящихся к области организации, планирования и управления строительством, требующих оптимизации получаемого решения.
Для каждой из пяти задач необходимо определить:
1. Критерий оптимизации.
2. К какой математической форме относится задача.
3. Каким методом задача может быть решена.
4. Какая проблема решается.
5. Почему для описания рассматриваемой в задаче ситуации необходимо пользоваться математической моделью.
6. Как можно было бы применить результаты проведенного анализа на практике.
Контрольные вопросы для самопроверки