Асимптоты графика функции

Определение. Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.

Прямая называется асимптотой графика функциидля, если разность- бесконечно мала для.

Асимптоты функции

Вертикальные, , если хотя бы одно из двух предельных значений являются бесконечными

Невертикальные, если то уравнениеопределяет наклонную асимптоту. Еслито асимптотаявляется горизонтальной.

СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ

I.

1) область определения;

2) область значений;

3) наличие точек разрыва и их характер; определить невертикальные (наклонные и горизонтальные) асимптоты;

4) четность, нечетность (указать характер поведения графика функции);

5) периодичность;

6) нули (указать точки пересечения с осями координат).

II. Интервалы монотонности и экстремумы

1) определить интервалы монотонности;

2) определить критические точки І рода и значения функции в них;

3) указать точки экстремума.

III.Промежутки выпуклости и точки перегиба

1) определить промежутки выпуклости графика;

2) определить точки перегиба и значения функции в них.

ІV. Внести данные в таблицы.

V. Построить график функции в декартовой системе координат.

Пример 5.Дана функция. Найти.

Решение:

Продифференцировать левую и праву части, учитывая, что является функцией от.

.

Решим данное уравнение относительно :

.

Пример 6.Найти производную функции, заданной уравнением:

Решение:

тогда

Пример 7.Найти уравнение касательной и нормали к кривойв точке.

Решение:

Уравнение касательной: .

.

Уравнение касательной: .

Уравнение нормали: ,

- уравнение нормали.

Пример 8.Найти, если

Решение:

Пример 9.Вычислить

Решение:

Имеем неопределенность вида . Воспользовавшись правилом Лопиталя, получим:

Пример 10.Вычислить

Решение:

Имеем неопределенность вида . Воспользовавшись правилом Лопиталя, получим:

Пример 11.Исследовать функциюи построить ее график.

Решение:

1. Область определения:

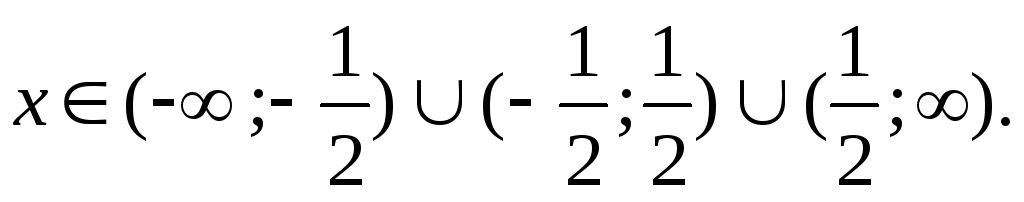
2. Функция имеет разрывы при

3. 

Ведь - вертикальная асимптота.

.Асимптоты

- вертикальные

Невертикальные

- горизонтальная асимптота.

4. Исследуем функцию на четность:

Функция является четной и ее график симметричен относительно оси Оу, функция непериодичная.

5. Интервалы монотонности и экстремумы:

Критические точки:

x	()		()	0	()		()
f /(x)	+	Не	+	0	–	Не	–
f(x)	возрастает	существует	возрастает	0	убывает	существует	убывает

– точка максимума:

6. Интервалы выпуклости и вогнутости, точки перегиба:

точек перегиба функция не имеет, так как в точке функция не определена:

x	()		()		()
f //(x)	+	Не	–	Не	+
f(x)	вогнутая	существует	выпуклая	существует	вогнутая

7. Построим график функции .

Пример 12. Найти наибольшее и меньше всего значения функциина отрезке

Решение

Имеем т.о.- критическая точка

Вычислим значения функции на концах отрезка:

Наименьшее значение функции равно –1 и принимается функцией во внутренней точке отрезка, а наибольшее значение равно 3 и принимается на левом конце отрезка.

Пример 13.Найти промежутки выпуклости кривойи точки перегиба.

Решение:

Находим

Здесь критической точкой является точка , где вторая производная имеет разрыв. Очевидно, что

на промежуткеи на этом промежутке функциявыпуклая вверх;

на промежуткеі на и на этом промежутке функциявыпуклая вниз;

Кривая имеет при точку перегиба