
- •22 Математический анализ
- •1. Функция
- •Способы задания функций
- •Свойства функций
- •Обратная функция
- •Сложная функция
- •2. Числовые последовательности
- •Свойства сходящихся последовательностей
- •3. Предел функции.
- •Односторонние пределы
- •Предел функции при х →∞
- •Бесконечно малая функция
- •Сформулируем некоторые теоремы о бесконечно малых функциях.
- •Для вычисления пределов надо пользоваться некоторыми правилами. Эти правила формулируются в виде теорем, которые мы сформулируем ниже. Для доведения этих теорем используется следующая теорема:
- •Следствие. Постоянный множитель можно выносить за знак предела:
- •Смысл производной
- •4. Дифференциал функции.
- •Геометрический смысл дифференциала
- •Основные теоремы дифференциального исчисления
- •5. Применение производной к исследованию функции и построения ее графика Монотонность функции
- •Максимумы и минимумы функции
- •Необходимое условие экстремума:
- •Наибольшее и наименьшее значение функции:
- •Выпуклость графика функции. Точки перегиба.
- •Асимптоты графика функции
- •Асимптоты функции
Для вычисления пределов надо пользоваться некоторыми правилами. Эти правила формулируются в виде теорем, которые мы сформулируем ниже. Для доведения этих теорем используется следующая теорема:
Теорема.
Для того чтобы функция у=f(х)
в точке х=х1
имела предел число
![]() необходимо и достаточно, чтобы она была
представлена в окрестности данной
точки в виде суммы
необходимо и достаточно, чтобы она была
представлена в окрестности данной
точки в виде суммы![]() ,
,
где![]() -бесконечно малаяфункция в окрестноститочких=х1
.
-бесконечно малаяфункция в окрестноститочких=х1
.
Теорема. Предел алгебраической суммы(разности) конечного числа функций, которые имеют предел в точке х=х0 , равен сумме(разности) пределов слагаемых:
![]()
Доказательство.
Пусть ![]() Тогда
по теореме о связи функции, ее предела
и б.м.в. можно записать:
Тогда
по теореме о связи функции, ее предела
и б.м.в. можно записать: ![]() и
и ![]() Следовательно
Следовательно
![]()

Следствие Функция может иметь только один предел при х→х1

Теорема. Предел произведения конечного числа функций, которые имеют пределы в точке х=х1 , равен произведению пределов сомножителей:

Следствие. Постоянный множитель можно выносить за знак предела:
 .
.
Следствие.Предел степени с натуральным показателем равен той же степени предела:
 ,
в частности
,
в частности
 ,
nN
,
nN
Теорема.
Если функция у=f(х)
имеет в точке х=х1
предел, отличный
от нуля, то функция
![]() - ограничена в окрестности данной точки.
- ограничена в окрестности данной точки.
Теорема. Предел частного двух функций, имеющих пределы, равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
 ,
если
,
если
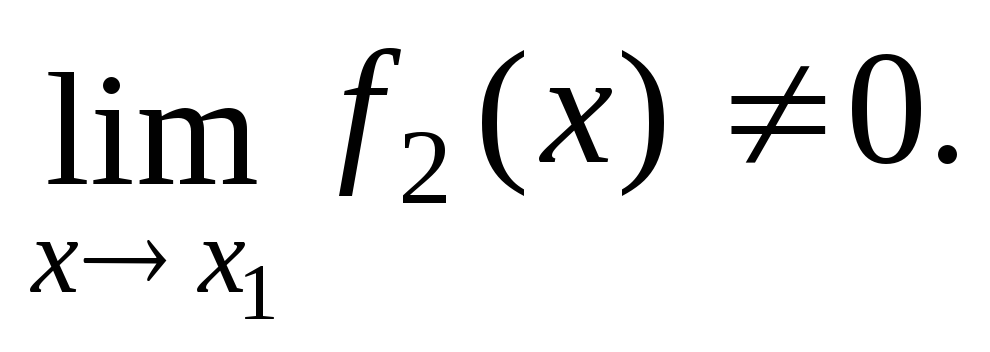
Сформулируем признака существования пределов:
Теорема.
Если значение функции f(х)
находится между соответствующими
значениями функций f1(х)
и f2(х),
которые при х=х1
стремятся к одному
пределу а,
то f(х)
при х=х1
также имеет предел число
![]() ,
т.е., если
,
т.е., если
![]()
и если

то

Свойства пределов
5.

Важные пределы
|
Первый замечательный предел |
Второй замечательный предел |
|
|
Эквивалентные бесконечно малые и основные теоремы о них
Среди бесконечно малых функций одного порядка особую роль играют так называемые эквивалентные бесконечно малые.
Если
![]() ,
то α и β называются эквивалентными
бесконечно малыми (при х → хо);
это обозначается так: α ~ β.
,
то α и β называются эквивалентными
бесконечно малыми (при х → хо);
это обозначается так: α ~ β.
Например, sin
х ~x при х → О, т. к![]() ;
tg х~ х при х→ О , т.к.
;
tg х~ х при х→ О , т.к.![]()
Применение эквивалентных бесконечно малых функций
Вычисление пределов
Для раскрытия
неопределённостей вида
![]() часто бывает полезным применять принцип
замены бесконечно малых эквивалентными
и другие свойства эквивалентных
бесконечно малых функций. Как известно,
sin х~x при х →х0, tg х~ х при х→ О.
Приведем еще примеры эквивалентных б.м
.ф.
часто бывает полезным применять принцип
замены бесконечно малых эквивалентными
и другие свойства эквивалентных
бесконечно малых функций. Как известно,
sin х~x при х →х0, tg х~ х при х→ О.
Приведем еще примеры эквивалентных б.м
.ф.
Пример.
![]()

Пример.
![]()

Пример.
![]()
Решение. Так как
 то
то
![]()
Ниже приведены важные эквивалентности, которые используются при вычислении пределов:

Пример.
![]()

3. Производная функции
При изучении различных материальных процессов, например движения тела, течения химических реакций, экономических процессов (спроса и затрат), мы встречаемся с задачей определения скорости изменения соответствующих величин. В большинстве случаев такие задачи не могут быть решены с помощью элементарной математики. Для их решения пользуются дифференциальным исчислением.
Итак, рассмотрим более детально задачу о прямолинейном движении некоторого твердого тела.
Предположим, что между пройденным телом путем и временами, за который пройден этот путь, существует зависимость S = f(t). (5.1)
Предположим также, что движение началось в т.0 при t=0(рис.1).
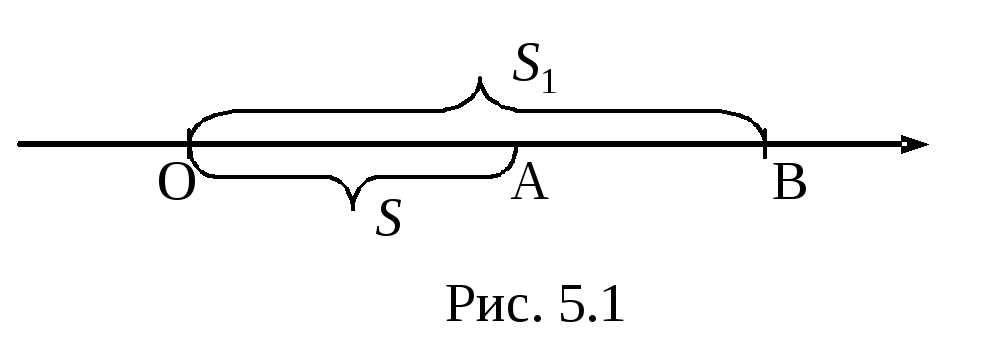
За время tтело прошло путьS = f(t)и оказалось в точкеА, а в следующий момент времениt+Δt оно оказалось в точкеВ. Обозначим путь, который прошло тело за времяt+Δt, через S1. Итак, за времяΔtтело прошло путь S1-S= f(t+ Δt)- f(t)Тогда средняя скорость движения тела на отрезкеАВбудет определяться по формуле (5.2)
![]() . (5.2)
. (5.2)
Но эта скорость не будет мгновенной
скоростью в момент t. Если говорят,
например, что поезд двигается со скоростью
100 км/ч, то это не означает, что он имеет
такую скорость все время, понятно, что
в начале движения и в конце его скорость
меньше. Чем меньше промежуток времени,
на котором измеряется средняя скорость,
тем ближе результат измерения к
фактической скорости в момент времениt. Итак, мгновенная скорость тела в
момент времениtбудет равна
![]() . (5.3)
. (5.3)
К такому же результату мы придем, если будем определять скорость химической реакции, скорость выпаривания вещества и т.п. Итак, разные с физической точки зрения задачи приводят к необходимости выполнения одинаковых с математической точки зрения действий, а именно, вычисления предела отношения приращения функции к приращению аргумента при условии, что последний стремится к нулю.
Приращением
функции f(х) в точке х0
называется разность между значением
функции в точке
![]() и ее значением в точкех0
и ее значением в точкех0
![]() .
.
Определение:
производной функции у=f(х)
в точке х называется предел отношения
приращения функции Δу в точке х к
приращению аргумента Δх, при условии,
что приращение аргумента стремится к
нулю![]() .
.
Дифференцирование функции f(х) - это операция нахождения ее производной.



