Модуль 5. Комплексные числа

Определения. Основные понятия.

Комплексными числами называют числа вида ,

где a и b – действительные числа, которые называются:

a – действительная часть комплексного числа ,

b - мнимая часть комплексного числа ,

i – мнимая единица (символ), причем i²=-1.

Множество комплексных чисел обозначают С. Любое действительное число а можно представить в виде комплексного: z=a+0·i

Отношения между комплексными числами

Комплексно - спряженные: .

, если

и - противоположны, если .

- ноль, - единица.

Геометрическая интерпретация

Комплексное число z=a+b·i можно изобразить:

• точкой М(a;b) координатной плоскости;

• радиус-вектором r=ОМ, проекции

x

которого на координатные оси соответственно:

хОу – комплексная плоскость;

Ох – действительная ось;

Оу – мнимая ось.

Модуль r комплексного числа z равен расстоянию от точки М(a;b) до начала координат

.

Аргумент комплексного числа – это угол, который образует радиус-вектор с положительным направлением оси Ох :

Главное значение аргумента удовлетворяет условию ―π < φ < π

Формы записи комплексных чисел

Алгебраическая	Тригонометрическая	Показательная
z=a+b·i	z=r(cosφ+i·sinφ)	z= r· еiφ

Формулы перехода.

a= r· cosφ	b = r·sinφ
;
;	,

r -модуль комплексного числа

φ - аргумент комплексного числа

Алгоритм нахождения аргумента

1. определить, в какой четверти находится точка z=a+b·i (использовать геометрическую интерпретацию комплексного числа);

2. найти в этой четверти угол , решив уравнения

Действия над комплексными числами в алгебраической форме

Пусть заданы два комплексных числа: и , тогда:

Сумма
Разность
Модуль разности		Изображает расстояние между точками и .
Произведение		Выполняют по правилу умножения многочленов, причем
Произведение комплексно-спряженных	.	Произведение комплексно - спряженных чисел равно сумме квадратов действительной и мнимой части комплексного числа.
Частное		Домножают числитель и знаменатель на число, комплексно-спряженное к знаменателю.

Действия над комплексными числами в тригонометрической форме

Пусть заданы два комплексных числа:

,

.

Произведение		При умножении модули перемножаются, а аргументы складываются.
Частное		При делении модули делят, а аргументы отнимают.
		При возведении в степень, модуль возводят в степень, а аргументы умножают на показатель степени.
Формула Муавра.
Корень n-й степени из числа где		Точки, которые соответствуют разным значениям корня, размещаются в вершинах правильного n - угольника с центром в точке О и имеют полярные координаты:.

Действия над комплексными числами в показательной форме

.

Формула Эйлера: е^iφ=(cosφ+i·sinφ).

Следствия:

Произведение z = z1 · z2	z = z1 · z2 = r1· r2· .
Частное .	.
Возведение в степень.
Извлечение корня n-й степени

Пример І. Изобразить на комплексной плоскости данные числа , , и выполнить действия: 1) ; 2); 3) , если ; ; .

Решение

Чтобы построить комплексное число необходимо на оси Ох отложить 5 – действительную часть комплексного числа; на оси Оу отложить 6 – мнимую часть (рис. 1). Потом построить вектор, который идет с начала координат к полученной точке. Этот вектор и будет изображением комплексного числа . Аналогично строим и .

Рис. 1

Выполним следующие действия над комплексными числами ,,:

1. Сложение, вычитание и умножение на число комплексных чисел в алгебраической форме выполняется по правилам алгебры.

.

2. Умножение двух комплексных чисел выполняется по правилам алгебры, учитывая, что :

.

3. Чтобы поделить два комплексного числа в алгебраической форме нужно числитель и знаменатель дроби умножить на число, спряженное к знаменателю (комплексно-спряженные числа - это такие числа, которые отличаются знаками только мнимой части).

.

Нужно учесть, что произведение двух комплексно-спряженных чисел равно сумме квадратов соответствующей действительности и коэффициента мнимой части, то есть.

Пример 2. Заданы два комплексных числа , .

1. Перейти от алгебраической к тригонометрической и показательной формам комплексного числа;

2. Выполнить следующие действия: 1) ; 2) ; 3) , 4) .

Решение

1. Алгебраическая форма комплексного числа имеет вид

, (1)

2. Тригонометрическая – , (2)

3. Показательная –. (3)

Чтобы перейти от алгебраической к тригонометрической и показательной форме, нужно определить модуль и аргумент комплексного числа по формулам:

, (4)

(5)

где - действительная часть комплексного числа, - мнимая часть комплексного числа.

Перейдем от алгебраической формы комплексного числа к тригонометрической и показательной форме.

Сначала запишем , . По формуле (4) определим модуль комплексного числа :

.

Изобразим комплексное число на комплексной плоскости (рис. 2).

Рис. 2.

Из рисунка видно, что аргумент . Найдем значение аргумента по формуле(5). Поскольку , то .

По формулам (2) и (3) соответственно запишем в тригонометрической и в показательной форме ,

.

Аналогично представим число в тригонометрической и в показательной форме (рис. 3) , .

.

Рис. 3

,

.

.

2. Выполним действия:

1) в тригонометрической форме.

Чтобы умножить два комплексных числа в тригонометрической форме, нужно перемножить их модули, а аргументы сложить:

.

2) в показательной форме.

Чтобы поделить два комплексных числа в показательной форме, нужно поделить их модули, а аргументы отнять.

.

3) в тригонометрической форме.

Чтобы возвести комплексное число в -ю степень, используется формулу Муавра .

.

В примере учтено то, что ; .

4) в показательной форме.

Чтобы извлечь корень - й степени из комплексного числа, используется формула , где .

.

, .

Если , то ;

; то .

то .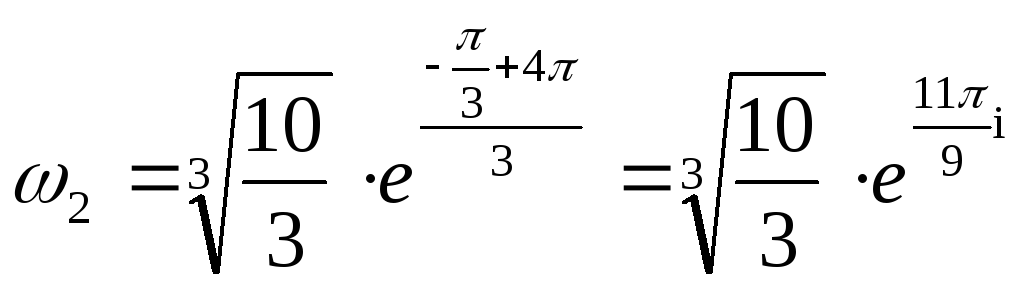

Пример 2. Найти действительные числа из условия равенства двух комплексных чисел:

Решение

.

Выделим в обеих частях равенства действительные и мнимые части:

Используя условие равенства двух комплексных чисел, составим систему:

Ответ:

Пример 3. Найти модуль и главные значения аргумента комплексных чисел:

Решение

а) , так как вектор, изображающий комплексное число, лежит на положительной полуоси Оу;

б) так как вектор, изображающий комплексное число, лежит на отрицательной полуоси Оу;

в)

г)

д)

или

е)

є)

.

Пример 4. Вычислить:

а)	в)
б)	г)