
Сб. тезисов Наукоемкие технологии 20 марта 2014
.pdf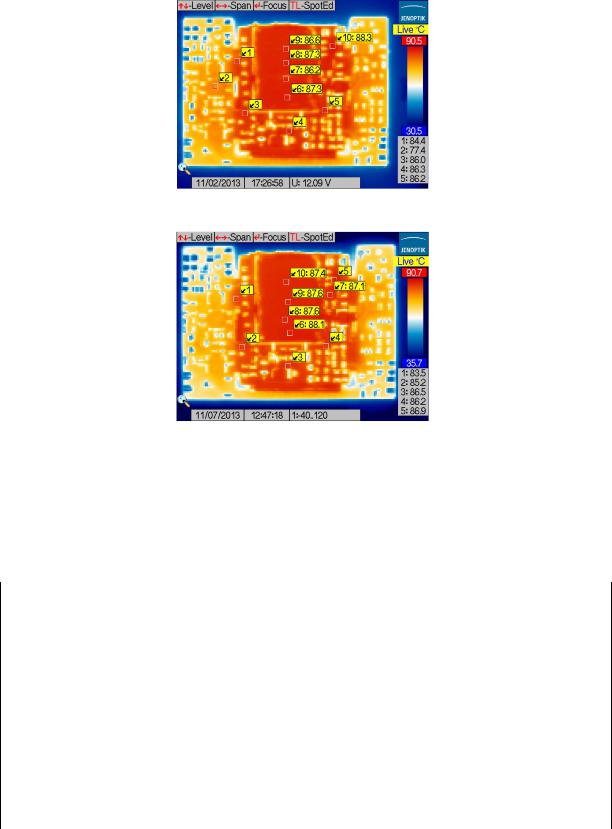
Рисунок 4 – Один слой лака с примесью сажи
Рисунок 5 – Два слоя лака с примесью сажи
Экспериментальные данные с примерами различных покрытий занесены в табл. 2.
Таблица 2 – Полученные опытные данные с применением различных покрытий
Покрытие |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Неокрашенный |
79 |
79,3 |
80,8 |
82,2 |
84,1 |
87,5 |
- |
- |
- |
- |
2 слоя: |
|
|
|
|
|
|
|
|
|
|
гуашь+лак |
77,9 |
79,6 |
79,8 |
82,4 |
82,2 |
84,8 |
80,1 |
80,3 |
80,5 |
80,7 |
Гуашь рез. |
80,5 |
81,8 |
82,3 |
82,7 |
- |
88,5 |
82,0 |
81,9 |
82,1 |
81,8 |
Гуашь+лак |
77,7 |
79,7 |
78,7 |
80,0 |
- |
85,7 |
78,8 |
80,4 |
80,5 |
80,4 |
Покрытие |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Неокрашенный |
1,1 |
-0,3 |
1 |
-0,2 |
1,9 |
2,7 |
- |
- |
- |
- |
2 слоя: |
|
|
|
|
|
|
|
|
|
|
гуашь+лак |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Гуашь рез. |
2,6 |
2,2 |
2,5 |
0,3 |
|
3,7 |
1,9 |
1,6 |
1,6 |
1,1 |
Гуашь+лак |
-0,2 |
0,1 |
-1,1 |
-2,4 |
|
0,9 |
-1,3 |
0,1 |
0 |
-0,3 |
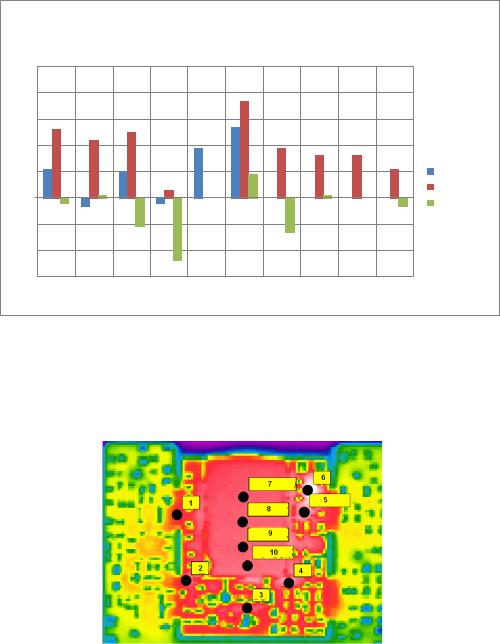
График зависимости температур от различных применяемых полимерных материалов, способа и количества нанесения окраски представлен на рис. 6.
121
|
Разницатемпературвразныхточкахгенератора№6294 |
|||||||||
|
|
|
взависимостиотспособаокраски. |
|
||||||
|
|
(Занулевуюлиниюпринятызначениятемпературприспособе2слояг+л) |
||||||||
|
5 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
С |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
температур, |
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Неокрашенный |
|
|
|
|
|
|
|
|
|
|
Гуашьрез |
|
Разница |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Гуашь+лак |
||
|
|
|
|
|
|
|
|
|
||
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
-3 |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
Номерточки |
|
|
|
|
|
Рисунок 6 – График зависимости температур от различных применяемых |
||||||||||
|
|
|
полимерных материалов и способа |
|
||||||
Оценка распределения температуры по заданным критическим точкам представлена на рис.7.
Рисунок 7 – Термограмма исследуемого генератора
Данный метод измерения тепловых характеристик показал положительный результат, но требует дальнейшей доработки.
Литература
1.Пономаренко В.П., Филачев А.М. Инфракрасная техника и электронная оптика: изд. 3-е, испр. и доп. – М.: Физматкнига, 2013.
2.Технические характеристики тепловизионной системы InfraTec VarioCAM hr head (Электронный ресурс) URL: http://www.diaworld.ru (дата доступа 01.03.2014)
3.ТУ 6-21-14-90. Лаки эпоксидно-уретановые УР-231 и УР-231Л.
122
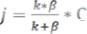
УДК 661.097.3
КРИТИЧЕСКИЕ ЯВЛЕНИЯ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ
Ш.О. Омаров, Е.А. Власов
Санкт-Петербургский государственный технологический институт (Технический университет)
Аннотация. Важным параметром при критическом условии воспламенения поверхности катализатора окисления является температура зажигания. В настоящей работе на основе теории теплового горения газовых смесей и экспериментальных данных по каталитическому окислению водорода рассчитаны температуры зажигания твердого катализатора.
Ключевые слова: температура зажигания, теплоотвод, критическое условие воспламенения.
При проведении экзотермических необратимых реакций в адиабатических реакторах полного смешения скорость выделения теплоты от температуры будет представлена в виде S-образной кривой, характер которой обусловлен совместным влиянием температуры и концентрации реагентов. Выше определенной температуры, называемой температурой «зажигания» (первое критическое явление), скорость реакции резко возрастает, увеличивается также и тепловыделение. При снижении температуры процесса скорость химической реакции при температуре «затухания» (второе критическое явление) резко уменьшается.
Температура зажигания является одной из важных характеристик катализатора и всего процесса. Ее можно определить как минимальную температуру, при которой каталитический процесс начинает идти с достаточной для практических целей скоростью. В стационарном режиме при температуре зажигания скорость выделения теплоты (для экзотермических реакций) становится равной скорости отвода теплоты (расходу теплоты на нагрев исходной реакционной смеси и выносу теплоты с продуктами реакции) [1,2]. Данная характеристика катализатора является чисто технической, и поэтому для каждого отдельного типа реактора для одного и того же катализатора она может быть разной.
В [1] показано, что для реакции, истинная кинетика на поверхности которой удовлетворяет первому порядку, скорость определяется уравнением:
, |
(1) |
123

где j – количество вещества, реагирующее на единице поверхности за единицу времени;
k – константа скорости гетерогенной реакции на поверхности катализатора;
β – коэффициент массоотдачи.
Стационарная температура поверхности, на которой идет реакция, может быть найдена как решение уравнения
(2)
где ∆Н – тепловой эффект химической реакции, Дж/моль; С – концентрация реагирующего вещества в объеме; α – коэффициент теплоотдачи, кДж/(м2×с×К).
Из соотношения (2) можно получить критическое условие воспламе-
нения
(3)
Известно, что
где α – коэффициент теплопроводности, м2/с; ср – изобарная удельная объемная теплоемкость, Дж/(м3×К); D – коэффициент диффузии, м2/с;
NuT NuD – критерии Нуссельта (тепловой и диффузионный).
Можно показать, что в (2)
Затем, подставляя эти соотношения в (2) и допуская, что NuT≈NuD (при отсутствии конвекции) и D = α, получим упрощенную формулу
(4)
Левая часть уравнения (4) показывает зависимость степени превращения окисляемого газа на поверхности катализатора, а на рис. 1 показано графическое решение уравнения (4).
В итоге получаем, что уравнение (4) в некотором приближении эквивалентно (2). В первом приближении можно принять, что решением (4) является уравнение (3), но при условии замены α на ср.
124
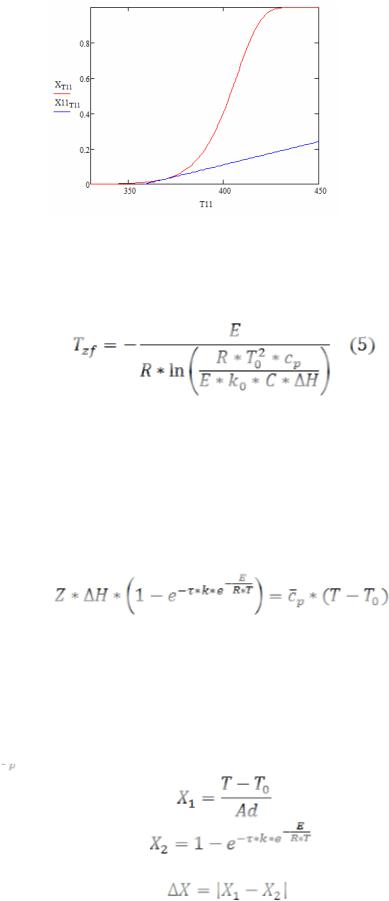
Рисунок 1 – Графическое решение уравнения (4)
Выражая из формулы (3) Т, получим уравнение для вычисления температуры зажигания Tzf:
где T0 – температура среды, куда происходит теплоотвод, К; Е – энергия активации процесса, Дж/моль;
R – универсальная газовая постоянная.
Определение температуры зажигания по зависимости X=f(T)
В этом методе для определения температуры зажигания получено решение уравнения, описывающее критическое условие воспламенения
(4):
(6)
Графическим решением этого уравнения является точка пересечения или касания S-образной кривой (левая часть) с прямой линией (правая часть уравнения). Для расчета температуры зажигания нас интересует только точка касания (рис. 1).
Поиск решения производился программным расчетом. Необходимо было вычислить два значения степени превращения Х по уравнениям (Аd=Z× ∆H/ 
 – адиабатический коэффициент):
– адиабатический коэффициент):
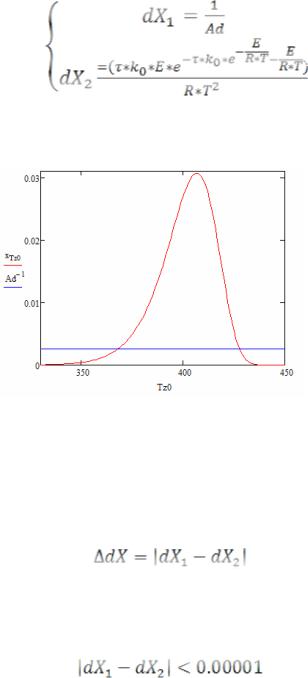
(7)
и далее найти минимальную абсолютную разность:
(8)
125
Как следует из уравнений (7), при расчете Х1 необходимо знать начальную температуру газовой смеси (Т0), которая затем возрастает до Т, осуществляя таким образом теплоотвод от поверхности разогретого катализатора. Для избавления от этой неопределенности оба уравнения были продифференцированы по температуре:
(9)
Графическое решение этой системы уравнений показано на рис. 2.
Рисунок 2 – Графическое решение уравнения (9)
Как видно из рис. 2, имеется две точки пересечения: левая определяет температуру зажигания, правая – температуру затухания.
Суть программного расчета заключалась в нахождении минимальной разности, в соответствии с уравнением (10), только вместо значений X брались значения dX, вычисляемые по формулам (9):
(10)
Так как при расчете изменяли температуру процесса, то в программе задавали цикл, изменяющий температуру с шагом 0,01 градуса, и далее вычисляли разность по уравнению (10) для каждой температуры, которая, с достаточной точностью анализа, должна удовлетворять неравенству:
(11)
После расчета получили массив температур, отвечающих условию (11), из которого находили среднее арифметическое, что и принималось за температуру зажигания Tz.
126
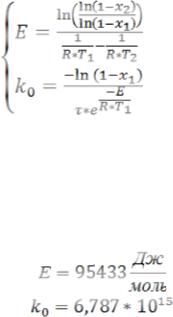
Пример расчета Tz катализатора окисления водорода
Этапы расчета:
1)Расчет энергии активации Е и коэффициента k0.
2)Расчет времени контакта газовой смеси с навеской катализатора.
3)Вычисление адиабатического коэффициента Ad.
4)Подстановка получившихся значений в систему уравнений (9) и программный поиск решения (в MathCad или в специальной программе).
Первоначально проводился эксперимент для снятия S-образной кривой: Х=f(T) на алюмооксидном катализаторе, содержащем 0,5 масс.% Pd. Опыты проводили при расходе газовой смеси Vp= 60 дм3/ч, объеме навески катализатора V= 4 см3, средней начальной концентрации водорода (C(вх)) в газовой смеси – 0,493 об. %, начальная температура – 296,15 К.
Таблица 1 – Изменение концентраций и степени окисления Н2 в зависимости от температуры (рис.3)
T, K |
C(вх), об.% |
С(вых), об.% |
Х, % |
296,15 |
0,430 |
0,380 |
11,6 |
298,15 |
0,496 |
0,415 |
16,3 |
303,15 |
0,496 |
0,299 |
39,7 |
315,15 |
0,507 |
0,064 |
87,4 |
323,15 |
0,507 |
0,024 |
95,3 |
329,15 |
0,534 |
0,012 |
97,8 |
331,15 |
0,480 |
0,005 |
98,9 |
Из табл. 1 взяли первые две точки, так как предположительно между ними лежит Tz.
Далее составили систему уравнений для вычисления Е и k0:
(12)
В уравнения (12) подставили выбранные значения T1, T2, x1, x2. Исходя из прямолинейного участка кривой в интервале температур
300-315К, несколько раз выбирали определенные значения Ti, xi. Вычислив значения Е и k0 для 7 промежутков, при их усреднении
получили следующие значения:
127
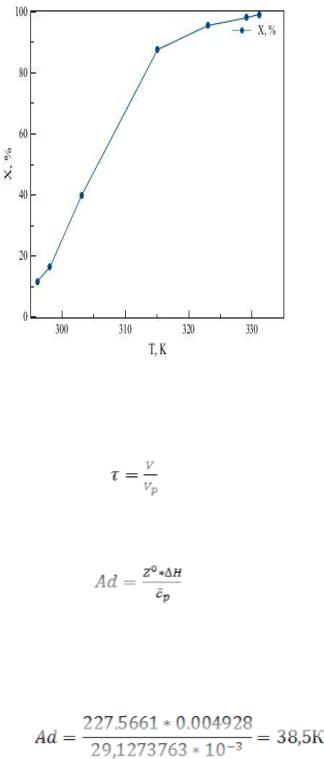
Рисунок 3 – Изменение степени окисления в зависимости от температуры
Расчет времени контакта газовой смеси с катализатором производили по уравнению (13):
(13)
и для данных условий эксперимента получили τ=0,24 c.
Вычисление адиабатического коэффициента производили по уравне-
нию
(14)
Для упрощения расчетов использовали средние значения энтальпии реакции и изобарной мольной теплоемкости на данном промежутке температур: ∆Н = 227,5661 кДж/моль (в расчете на 1 моль водорода);
ср = 29,1273×10-3 кДж/(моль×К) [3].
Тогда
Графически решение нахождения Т, при которой будет выполняться условие системы (9) представлено на рис. 4: Tz = 317 K.
Если ранее было неизвестно значение начальной температуры газовой смеси (T0), то теперь ее можно вычислить, преобразовав уравнение (6) к следующему виду:
128
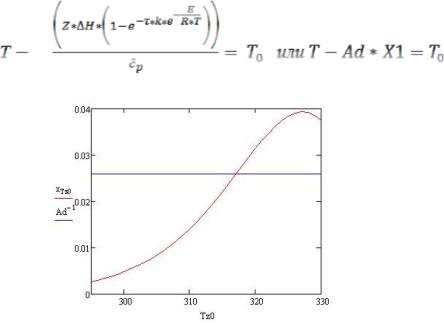
(15)
Рисунок 4 – Графическое определение температуры воспламенения при окислении водорода
Подставив вместо Т найденное выше Tz и все остальные параметры,
получим T0 = 306,845К.
Подставив значение T0 в (4), получимTzf = 302,069 К.
Зависимости Tz от концентрации водород
Из анализа системы уравнений (9) можно сделать вывод о зависимости Tz от начальной концентрации окисляемого водорода при постоянной объемной скорости газового потока. Действительно, в табл. 2 показаны полученные по разработанному нами методу и по уравнению (5) значения Tz в зависимости от изменения концентрации водорода.
Таблица 2 – Значения Tz по методу Х=f(Т) и по формуле (5)
C, об.% |
Tz, К |
Tzf, К |
0,4 |
320,36 |
303,85 |
0,5 |
316,92 |
301,94 |
1,0 |
309,01 |
296,21 |
1,5 |
305,09 |
292,96 |
2,0 |
302,47 |
290,71 |
2,5 |
300,51 |
288,98 |
3,0 |
298,94 |
287,59 |
3,5 |
297,64 |
286,43 |
4,0 |
296,52 |
285,42 |
4,5 |
295,55 |
284,55 |
5,0 |
294,69 |
283,77 |
129
Анализ проведен только для макроконцентраций водорода:
С% > 0,3 об.%,
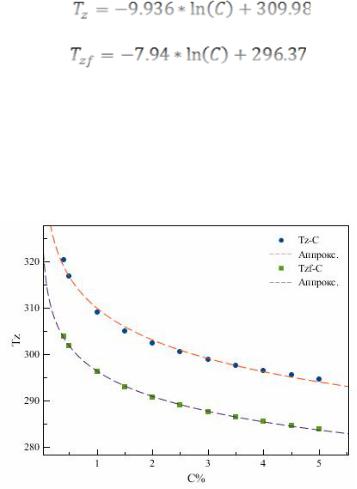
так как для таких концентраций, вследствие неизменности механизма окисления [4], можно принять Е и k0 постоянными величинами. Точки Tz=f(С) аппроксимированы зависимостью
(16)
Точки функции Tzf=f(С) аппроксимированы зависимостью (17):
(17)
Точность аппроксимации составила более 99%.
Из уравнения (5) следует, что Tz фактически зависит как от концентрации окисляемого газа, так и от T0. Из проводимых опытов нельзя экспериментально определить конкретное значение Т0 в момент зажигания, поэтому Т0 вычисляли по уравнению (15) и подставляли в (4).
Аппроксимация результатов эксперимента показана на рис. 5.
Рисунок 5 – Кривые аппроксимации результатов эксперимента
Как видно из представленных данных (рис.5), разница между результатами вычисления Tz не превышает 5,2 К. При необходимости повышения точности расчета, по-видимому, следует учесть конвективные эффекты при выводе соотношения (4), а также более надежное экспериментальное определение температуры поверхности катализатора.
Таким образом, предложенная методика расчета параметра воспламенения газовой смеси (температуры зажигания), хорошо согласуется с экспериментальными данными окисления водорода.
Литература
1.Голодец Г.И. Гетерогенно-каталитические реакции с участием молекулярного кислорода. – Киев: Наукова думка, 1977. 360 с.
130
