Зачет матан 1 семестр

68)Условием существования и единственности обратной матрицы

является то,что матрицы A и A−1 должны быть квадратными и причем одного и того же порядка.

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть ее определитель не равен нулю ( ≠0) .

Для такой матрицы A существует следующая обратная матрица:

­знак транспонирования.

70)A * X = B, где A­ основная матрица системы, B и X ­ столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на

A−1 − матрицу,обратную к матрице A : A−1 * (AX) = A−1 * B.

Так как A−1 * A = E, получаем X = A−1 * B. Пример решения.

1.Вычислим алгебраические дополнения для элементов матрицы, состоящей из коэффициентов при неизвестных

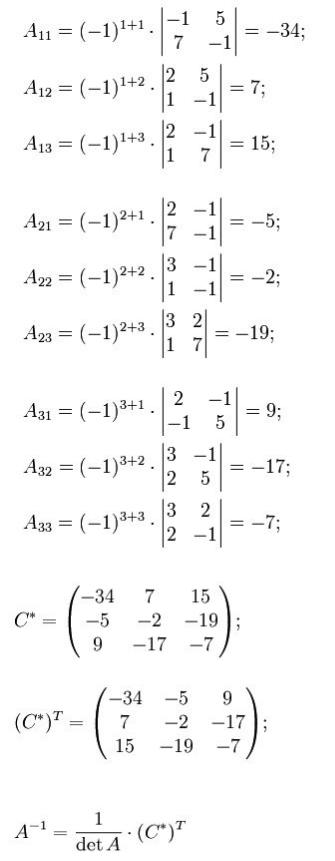
2.Транспонируем матрицу

3.Подставим переменные в формулу

получим:

4.Найдем неизвестные.Для этого перемножим обратную матрицу и столбец

Ответ: X=2, Y=1, Z=4.

71) Базисный минор матрицы. Определение.

Базисный минор матрицы ­ каждый отличный от нуля минор, порядок которого равен рангу данной матрицы

72) Ранг матрицы. Определение Ранг матрицы А есть наибольшийпорядокееминоров, отличныхотнуля. Обозначается r(A)

73) Теорема о базисном миноре:

74)​Система линейных алгебраических уравнений. Общие понятия​.

Совокупность уравнений Совокупность уравнений

относительна неизвестных x1, x2, ..., xn­1, xn называется ​системой

линейных алгебраических уравнений.

Числа aij — коэффициентысистемы,bi— правыечастисистемы i=1,2, ..., m; j = 1, 2, ..., n.

Совокупность значений неизвестных, удовлетворяющая всем уравнениям системы, называется ​решением системы​.

Система, имеющая хотя бы одно решение, называется совместной. Система, у которой нет решений, называется ​несовместной​.

Каждое решение совместной системы называется ​частным решением. Совокупность всех решений совместной системы называется ​общим решением​.

Если среди правых частей bi системы есть хоть одна, отличнаяотнуля, то система называется ​неоднородной​системой линейных уравнений.

Если все правые части системы равны нулю, то система называется

однородной​.

75) ​Теорема Крамера

Пусть задана система n уравнений с n неизвестными

A – матрица этой системы, а B – столбец свободных членов

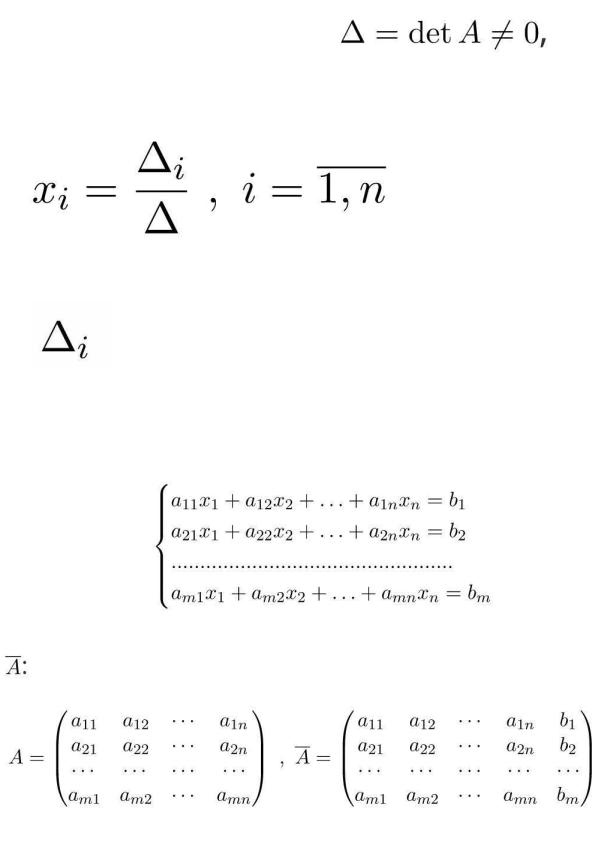
Если определитель матрицы системы ,​то системы линейных уравнений (1) имеет единственное решение, которое вычисляется по формулам

где – определителиматриц, которыеполучаютсяизматрицы A заменой i­го столбца на столбец свободных членов​B.

76)​Теорема Кронекера­Капелли

Рассмотрим систему n линейных алгебраических уравнений (СЛАУ) с m

неизвестными:

Выпишем основную матрицу этой системы A и расширенную матрицу

ТЕОРЕМА!!! ​СЛАУ совместна тогда и только тогда,

когда ранг её основной матрицы A равен рангу её

расширенной матрицы

Причём система имеет единственное решение, если ранг равен числу

77)​Каноническое уравнение эллипса. Геометрический смысл

коэффициентов

Каноническим уравнением эллипса (в канонической системе координат)

В этомслучаеосикоординатявляютсяосямисимметрииэллипса, аначало координат является его центром симметрии.

Вершинами эллипса​являются ​точки​A1(a,0), A2(­a,0), B1(0,b) и B2(0,­b).

Если параметры a и b удовлетворяют условию a > b, то они называются соответственно ​большой и малой полуосью​эллипса.

Расстояние от начала координат до фокусов равно c и определяется

соотношением .​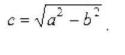

Если параметры a и b удовлетворяют условию a < b, то фокусы эллипса

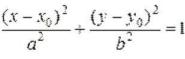
расположены на оси Oy в точках F1(0, c) и F2(0, ­c), а .​ Если центр эллипса смещен относительно начала координат в точку

Приведение общего уравнения эллипса к нормальному виду проводится

методом выделения полных квадратов по переменным x и y.

78) Каноническое уравнение окружности:

X^​2​+Y^​2​=R​^2

79) Уравнение гиперболы:

(x^2/a^2)­(y^2/b^2)=1

​Геометрический смысл коэффициентов в уравнении гиперболы:

Найдем точки пересечения гиперболы с осью абсцисс (вершины гиперболы). Подставляя в уравнение y=0, находим абсциссы точек пересечения: x=​+​a. Следовательно, вершины имеют координаты (­a,0),(a,0). Длина отрезка, соединяющеговершины, равна 2a. Этототрезок называется действительной осью гиперболы, а число a — действительной полуосью гиперболы. Подставляя x=0, получаем y=​+​ib. Длинаотрезкаоси ординат, соединяющего точки (0,­b),\,(0,b), равна 2b. Этот отрезок называется мнимой осью гиперболы, а число b — мнимой полуосью гиперболы. Гипербола пересекает прямую, содержащую действительную ось, и не пересекает прямую, содержащую мнимую ось.

80)​Уравнение параболы: y^2=2px, где р> 0

81) Многочлены. Теорема Безу

Многочленом n – ой степени относительно переменной x называется выражение: anxn + an−1xn−1 + an−2xn−2 + ... + a1x1 + a0 = 0

Теорема Безу. ​Еслимногочлен P(x) разделитьна (x­a), тоостатокот деления равен P(a).

Следствия: 1) число a является корнем многочлена P(x) тогда и только тогда, когда P(x) кратно (x − a) .

3) Число различных корней многочлена степени n не больше, чем

его степень. Число a называется корнем кратности k, если

P(x) = (x − a)k

82.​Формулировка Основной теоремы алгебры: ​любой многочлен нулевой степени имеет хотя бы один комплексный корень

83.​Комплексные числа ­ числа вида X+Yi, где X и Y ­ вещественные числа, i ­ мнимая единица (величина, для которой выполняетсяравенство: i^2= ­1). множество упорядоченных парвещественныхчисел, видкоторых определен операциями умножения, сложения и т.д

Z=x+yi

84.Алгебраическая форма комплексного числа: Z=x+yi

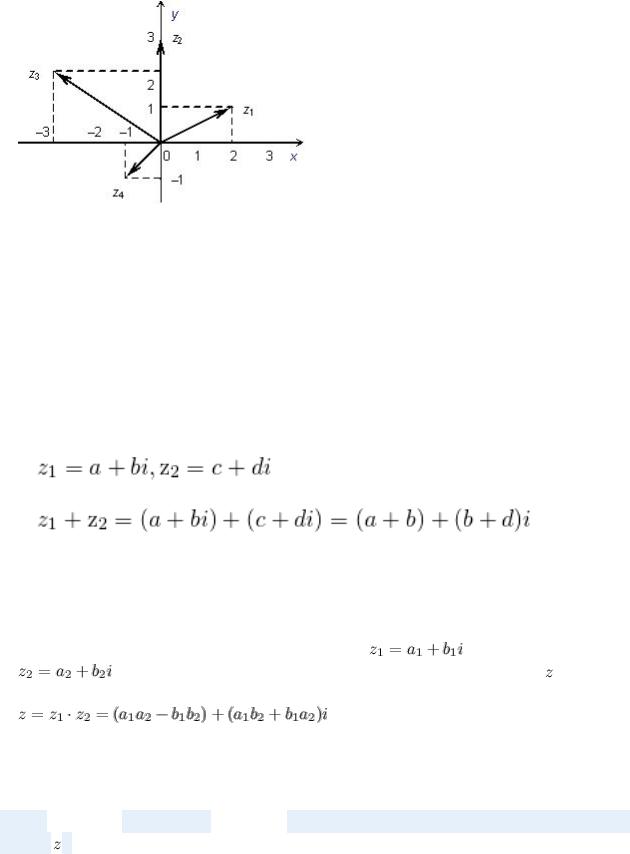
85)​Изображение комплексного числа на комплексной плоскости

Изобразим на комплексной плоскости числа , , , ​, ​: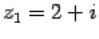

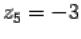86)​Операция сложения комплексных чисел в алгебраической форме

Сумма двух комплексных чисел, записанных в алгебраической форме, — этокомплексноечисло, действительнаячастькоторогоикоэффициентпри мнимой части равны соответственно сумме действительных частей и сумме коэффициентов при мнимых частях слагаемых.

Сложение комплексных чисел в алгебраической форме

можно записать с помощью формулы:

87)​Умножение комплексных чисел в алгебраической форме

.

88 ​Комплексно сопряженные числа.Изображение на комплексной

плоскости.

Если ,​то число называется комплексным сопряженным к числу ​.

То есть у комплексно сопряженных чисел действительные части равны, а мнимые отличаются знаком.

На комплексной плоскости комплексно сопряжённые числа получаются зеркальным отражением друг друга относительно действительной оси. Комплексно­сопряженные числа на плоскости изображаются точками, симметричными относительно оси Ox; противоположные комплексные числа — точками, симметричными относительно точки O (начала координат).Например,

89 Деление комплексных чисел в алгебраической форме.Алгоритм.

На практике деление комплексных чисел проводят по следующей схеме:

1.сначала делимое и делитель умножают на число, ​комплексно сопряженное делителю, после чего делитель становится действительным числом;