MEHANIKA

Здесь учтено, что произведение плотности на объем тела равно его массе, а в качестве скорости использована скорость центра масс тела, поскольку она такая же, как и скорость любой другой точки. Таким образом, при поступательном движении тела его кинетическая энергия рассчитывается по формуле аналогичной формуле (4.45) для кинетической энергии материальной точки.

Рассмотрим теперь вращательное движение твердого тела (рис. 26). Бесконечно малый элемент, находящийся на расстоянии h =

где использовано выражение (4.25) для момента инерции тела относительно оси вращения. Полученное соотношение показывает, что при поступательном и вращательном движениях кинетическая энергия тела вычисляется схожим образом (формулы (4.48) и (4.49)). Аналогия, отмеченная при анализе количественных характеристик поступательного и вращательного движений, сохраняется и здесь.

При плоскопараллельном движении твердого тела его полная кинетическая энергия складывается из кинетической энергии поступательного и кинетической энергии вращательного движения вокруг полюса. Если в качестве полюса вновь выбрать центр масс твердого тела, то для вычисления полной кинетической энергии при этом виде движения следует объединить соотношения (4.48) и (4.49):

Здесь Jz – момент инерции твердого тела относительно оси, перпендикулярной плоскости движения и проходящей через центр масс.

Выясним теперь, за счет чего может измениться величина кинетической энергии механической системы. Для этого рассмотрим сначала одну материальную точку. Движение материальной точки подчиняется уравнению (4.1): m W = F, где F – равнодействующая всех сил, действующих на точку. Умножим обе части этого уравнения скалярно на вектор скорости точки:

81

mW V = F V.

Правая часть полученного равенства, согласно (4.35), равна мощности N сил, действующих на точку. Левая часть может быть преобразована следующим образом:

Следовательно, производная по времени от кинетической энергии материальной точки равна алгебраической сумме мощностей всех сил, действующих на точку (или мощности их равнодействующей):

В случае механической системы, состоящей из n материальных точек, предыдущее утверждение справедливо для каждой из точек:

Просуммируем левые и правые части всех этих равенств. Тогда слева, согласно (4.46), получим полную кинетическую энергию механической системы, а справа – сумму мощностей всех действующих в системе сил:

Следовательно, производная по времени от кинетической энергии механической системы равна алгебраической сумме мощностей всех сил, действующих в системе. Это означает, что скорость изменения кинетической энергии определяется величиной мощности всех сил, вызывающих движение.

Соотношение (4.52) справедливо для данного момента времени. Если требуется установить, насколько изменилась кинетическая энергия тела за некоторый конечный промежуток времени от 1 до 2, то предыдущее равенство нужно проинтегрировать по времени в пределах указанного промежутка:

82

В правой части этого соотношения, согласно (4.37), получим алгебраическую сумму работ всех действующих на тело сил, а в левой части – изменение полной кинетической энергии тела за промежуток времени ( 1 , 2): Т = Т( 2) – Т( 1). Таким образом, изменение кинетической энергии механической системы за некоторый конечный промежуток времени равно алгебраической сумме работ всех сил:

Сформулированное утверждение является одним из наиболее важных в механике, поскольку оно справедливо для любого вида движения твердого тела.

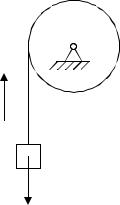
В качестве иллюстрации эффективности использования энергетического подхода рассмотрим следующую задачу. Пусть требуется определить силу натяжения каната подъемной машины в начальный момент подъема груза, когда он приходит в движение из состояния покоя (рис. 28). Будем считать известными массу груза m, момент инерции барабана J и его радиус R, а также величину вращающего момента М, приложенного к барабану.

М

W

Рисунок 28

mg

Решение. Полная кинетическая энергия системы «барабан-груз» в любой момент времени складывается из кинетической энергии груза и кинетической энергии барабана. Груз движется поступательно, его кинетическая энергия определяется соотношением (4.48). Кинетическая энергия вращающегося барабана вычисляется с помощью формулы (4.49). Следовательно, полная кинетическая энергия Т системы равна:

83

Здесь использовано соотношение (3.24), связывающее линейную скорость V при вращательном движении с угловой скоростью .

Воспользуемся равенством (4.52) для скорости изменения кинетической энергии. Левая часть этого равенства в условиях рассматриваемой задачи равна:

Определим теперь сумму мощностей всех сил, действующих в системе «барабан-груз». К указанным усилиям относятся вес груза, вращающий момент, вес барабана и опорная реакция. Две последние силы мощности не имеют, поскольку приложены к неподвижным точкам. Найдем мощности веса груза и вращающего момента. Вес груза, согласно (4.35), имеет мощность N = - mgV. Знак минус учитывает то обстоятельство, что сила веса направлена в сторону, противоположную направлению движения. Вращающий момент, согласно (4.41), имеет мощность N = M = MV / R. Сумма мощностей будет, таким образом, равна:

Приравнивая полученный результат и правую часть (4.54), для ускорения груза имеем:

В соответствии с принципом Даламбера (подраздел 4.3) натяжение каната равно сумме веса груза и силы инерции: ( mg + mW ) = mg ( 1 + W / g ). Отсюда видно, что влияние силы инерции определяется величиной ускорения груза по сравнению с величиной ускорения свободного падения.

4.11. Динамика простейших колебательных систем

Колебательные движения играют огромную роль при эксплуатации химического оборудования. Чаще всего инженер-технолог сталкивается с частным видом колебаний – вибрациями (колебания с

84

малой амплитудой, но большой частотой). С точки зрения работоспособности технологических машин и аппаратов вибрации крайне нежелательны, поскольку оборудование при этом испытывает переменные во времени циклические нагрузки. Большинство конструкционных материалов сопротивляется таким нагрузкам гораздо хуже, чем статическим.

В подразделе 4.2. уже рассматривалось колебательное движение материальной точки, но проведенный анализ был неполным и привел к результату, противоречащему практике. Причина противоречия заключалась в том, что анализ не учитывал сил сопротивления. Любая реальная колебательная система состоит из нескольких обязательных составляющих: упругого элемента, источника вынуждающей силы, инерционного элемента (принципиальная схема простейшей колебательной системы приведена на рис. 29). Упругий элемент порождает появление упругой силы Fупр, которая, как уже отмечалось ранее, в любой момент времени направлена в сторону нейтрального недеформированного положения, и величина которой пропорциональна расстоянию до него. Вынуждающая сила F( ) является внешней причиной колебаний. Она, как правило, периодически меняется во времени. Инерционный элемент определяется массой колебательной системы m. Он вызывает появление сил инерции.

c

m F(τ)

k

Рисунок 29

В реальных колебательных системах, помимо перечисленных сил, всегда существуют силы, препятствующие поддержанию движения. Это силы трения и силы гидравлического сопротивления. Если колебания элементов оборудования особенно нежелательны, то в конструкции вводятся специальные устройства, предназначенные для демпфирования (подавления) колебаний. В любом случае сила сопротивления Fсопр пропорциональна скорости движения колеблющегося тела и направлена в сторону, противоположную направлению движения.

Приведенные предварительные замечания позволяют перейти к описанию поведения колебательных систем. Основой описания является уравнение движения (4.17), в котором за центр масс принят

85

центр масс колеблющегося тела. Пусть движение происходит в горизонтальном направлении вдоль координатной оси Ох. Совместим начало координат с положением центра масс при нейтральном состоянии колебательной системы и спроектируем уравнение на координатную ось. При этом проекция силы тяжести инерционного элемента будет равна нулю. В результате получим:

m dd2 x2C F( ) Fсопр Fупр

Сила сопротивления с учетом сделанных замечаний может быть

сопротивления), а сила упругости пропорциональна координате х: Fупр = - с х (с – коэффициент упругости или жесткости). Вынуждающая сила при гармоническом характере внешних воздействий может быть аппроксимирована следующим выражением: F( ) = F0 sin ς , где ς – частота колебаний возмущающей силы. Подставляя все выражения для сил в предыдущее уравнение, получим дифференциальное уравнение, описывающее движение центра масс простейшей колебательной системы:

Это уравнение сводится к уравнению свободных незатухающих колебаний (4.5) при отсутствии вынуждающей силы (F0 = 0) и сопротивления движению (k = 0). При этом инерционный элемент

будет совершать колебания (4.6) с частотой mc , которая

называется собственной частотой колебаний колебательной системы.

Учет сил сопротивления в уравнении (4.55) в условиях отсутствия вынуждающей силы (k 0, F0 = 0) приведет к однородному дифференциальному уравнению второго порядка с постоянными

Непосредственной подстановкой нетрудно убедиться, что общим решением этого уравнения является функция:

86

где А1 и А2 – постоянные интегрирования, значения которых находятся

сил сопротивления. Функция (4.57) описывает затухающие колебания, поскольку сомножитель перед скобкой убывает с течением времени. Причем, при центр масс колеблющегося тела неограниченно приближается к началу координат, т. е. к положению равновесия. При этом, чем большей инерционностью обладает колебательная система, тем медленнее происходит затухание колебаний. Таким образом, влияние сил сопротивления проявляется двояко: в смещении частоты колебаний и в их полном подавлении с течением времени.

Рассмотрим теперь наиболее важный для практики случай, когда колебания обусловлены действием вынуждающей силы. Для простоты будем пренебрегать силой сопротивления, поскольку их эффект уже проанализирован. В этом случае общее уравнение (4.55) примет вид:

Из курса математики известно, что общим решением уравнений такого вида является сумма общего решения соответствующего однородного уравнения (с нулевой правой частью) и частного решения неоднородного. Общее решение однородного уравнения получено ранее. Оно задается соотношением (4.6). Частное решение неоднородного уравнения будем искать в виде:

Подставляя это выражение в уравнение (4.58), после несложных преобразований убеждаемся, что функция (4.59) будет удовлетворять уравнению, если величина коэффициента В равна:

B F0 . m( 2 2 )

Следовательно, общее решение уравнения (4.58), описывающее закон движения центра масс колебательной системы при вынужденных колебаниях, будет иметь вид:

87

Из полученного решения видно, что вынужденные колебания складываются из двух движений: из чисто вынужденных колебаний

(первое слагаемое в (4.60)) и из сопровождающих колебаний

(второе и третье слагаемые). Чисто вынужденные колебания происходят с частотой вынуждающей силы, в то время как частота сопровождающих колебаний определяется свойствами самой колебательной системы. При совпадении указанных частот сомножитель в первом слагаемом обращается в бесконечность. В реальности с учетом сил сопротивления это означает, что амплитуда колебаний становится значительно больше, чем при несовпадении частот вынужденных и собственных колебаний. Это явление называется резонансом.

Достижение резонанса, как правило, приводит к разрушению механической системы. Поэтому при эксплуатации химического оборудования, когда возникают колебания некоторых его элементов, резонанса пытаются всячески избежать. Это можно сделать с помощью ряда мер, которые непосредственно подсказывает вид решения (4.60). Например, можно снизить амплитуду вынуждающей силы, уменьшив величину F0, за счет улучшения балансировки движущихся узлов оборудования. Иногда удается избежать резонанса путем изменения собственной частоты системы. Поскольку

собственная частота равна mc , это можно сделать, изменив

массу колеблющихся элементов оборудования или жесткость упругих элементов. Еще один путь – установка специальных демпферов, гасящих колебания.

4.12.Контрольные вопросы

1.Что изучает динамика ?

2.В чем состоят первая и вторая задачи динамики ?

3.В чем смысл первой аксиомы динамики ?

4.Сформулируйте основной закон механики.

5.Запишите дифференциальное уравнение движения материальной точки.

6.Запишите дифференциальное уравнение движения материальной точки в естественных осях.

7.Что такое сила инерции и от чего зависит ее величина ?

8.Сформулируйте принцип Даламбера. В чем состоит его смысл ?

88

9.Чему равны нормальная и касательная составляющие силы инерции для вращающегося тела ?

10.Что такое центр масс механической системы ?

11.Как вычисляется скорость и ускорение центра масс ?

12.Запишите дифференциальное уравнение поступательного движения твердого тела.

13.Что такое количество движения механической системы ?

14.Сформулируйте теорему об изменении количества движения механической системы.

15.Как определяется импульс силы за некоторый промежуток времени ?

16.В чем состоит содержание теоремы импульсов ?

17.Могут ли внутренние силы, действующие в механической системе, изменить ее количество движения ?

18.Как определяется момент инерции механической системы и твердого тела относительно некоторой оси ?

19.Что такое момент количества движения механической системы ?

20.Существует ли аналогия между количественными характеристиками поступательного и вращательного движения ?

21.За счет чего может измениться кинетический момент механической системы ?

22.Запишите дифференциальное уравнение вращательного движения твердого тела.

23.Запишите дифференциальное уравнение плоскопараллельного движения твердого тела.

24.Как определяется мощность силы ? От чего она зависит ?

25.Как определяется работа силы за некоторый промежуток времени ?

26.Могут ли мощность и работа силы принимать отрицательные значения ?

27.Чему равна работа сил при вращении твердого тела ?

28.Чему равна работа силы тяжести ?

29.Что такое кинетическая энергия механической системы ?

30.Чему равна кинетическая энергия при поступательном движении твердого тела ?

31.Чему равна кинетическая энергия при вращательном движении ?

32.За счет чего может измениться кинетическая энергия механической системы ?

33.Чему равно изменение кинетической энергии механической системы за некоторый промежуток времени ?

34.Какие элементы включает простейшая колебательная система ?

35.Какие силы учитываются при анализе колебательных систем ?

36.Запишите дифференциальное уравнение движения центра масс колебательной системы.

37.Что такое резонанс, в чем он выражается ?

89

5. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ЭЛЕМЕНТАХ ОБОРУДОВАНИЯ, МОДЕЛИРУЕМЫХ В ФОРМЕ СТЕРЖНЯ

Основная задача инженера технолога на химическом предприятии состоит в обеспечении безотказной работы оборудования, находящегося в сфере его ответственности. Безотказная работа оборудования означает, что оно находится в работоспособном состоянии, когда все параметры, характеризующие функционирование установки, аппарата или машины, находятся в пределах, установленных нормативно-технической документацией

(например, технологическим регламентом). Потеря работоспособности (отказ) может быть вызвана несколькими причинами (разрушением одного из элементов оборудования, недопустимо большими деформациями деталей, нарушением герметичности рабочего объема и т. д.). Каждая из этих причин связана, в конечном счете, с некоторыми изменениями в конструкционном материале под действием внешних нагрузок. Провести анализ таких изменений в рамках представлений об абсолютно твердом теле, конечно, нельзя. Поэтому в настоящем разделе и во всех последующих используется расчетная схема деформируемого тела.

5.1. Упругость, перемещения и деформации твердых тел

Абсолютно твердых недеформируемых тел, которые рассматривались в предыдущих разделах, на самом деле не существует. В процессе эксплуатации оборудования все его детали под действием внешних нагрузок и физико-химических воздействий изменяют свои первоначальные размеры и форму, то есть деформируются, корродируют, изнашиваются. Эти изменения при неограниченном возрастании указанных воздействий могут привести либо к разрушению конструкции, либо к недопустимому для дальнейшей эксплуатации искажению ее формы и размеров. Поэтому первое, с чего следует начать изучение поведения реальных тел под действием нагрузок, это введение количественных характеристик для изменений их размеров и формы.

Пусть при деформировании детали под действием сил некоторая точка М переместится в пространстве в новое положение М1. Вектор ММ1, имеющий начало в точке М недеформированного тела, а конец в той же точке М1 деформированного тела, называется вектором полного перемещения точки. Его проекции u, v, w на оси координат декартовой системы координат носят название перемещений точки по осям. Величина вектора перемещения и его направление при заданных нагрузках зависят от положения точки М.

Для характеристики интенсивности локального изменения размера и формы тела существует понятие деформации в точке. Мысленно

90