MEHANIKA

dm m аdxdz mdxdz hвв hв

С учетом того, что координата у = 0, интегрирование в формуле (4.25) сведется к интегрированию по координатам х и z в пределах их изменения:

Аналогично может быть получено выражение для момента инерции Jх относительно оси Ох. Оно равно Jх = mв2 / 12. Позднее нам понадобится значение момента инерции диска радиуса R и массы m относительно оси, проходящей через его центр. Он равен J = mR2/2.

Из приведенного примера видно, что величина момента инерции относительно некоторой оси зависит от квадрата поперечного по отношению к данной оси размера тела. Кроме того, она зависит от положения оси, относительно которой вычисляется момент инерции. С помощью аналогичных вычислений можно показать, что момент инерции относительно оси Оz параллельной Оz и отстоящей от нее на расстоянии р равен: Jz = Jz + mp2. Отсюда следует, что, зная значение момента инерции тела относительно некоторой оси, нетрудно определить его значение относительно любой оси, параллельной данной. Другой вывод, который может быть сделан:

момент инерции тела относительно оси, проходящей через центр масс (или центр тяжести), является наименьшим из всех моментов инерции относительно осей, параллельных ей.

4.7. Момент количества движения материальной точки и механической системы

При анализе сил, действующих на твердое тело, отмечалось, что вращательный эффект силы определяется ее моментом относительно некоторой точки или оси. Величина момента силы в общем случае находится по формуле (2.10) как векторное произведение радиусвектора, проведенного в точку приложения силы, на вектор самой силы: M(F) = r x F. Точно так же для количественного описания вращательного движения служит особая характеристика - момент количества движения. Она определяется аналогично понятию момента силы, а именно: моментом количества движения МО(mV) материальной точки относительно некоторой центра О называется векторное произведение:

71

Направление вектора МО(mV) определяется по обычным правилам для векторного произведения. Единицей измерения момента количества движения служит кг м2/с.

Моментом количества движения механической системы (или

кинетическим моментом) называется векторная сумма моментов количества движения всех точек, составляющих систему:

Здесь моменты количества движения всех материальных точек, составляющих систему, вычисляются относительно одного и того же центра О. В том случае, когда механическая система представляет собой твердое тело, суммирование в формуле (4.27) заменяется на интегрирование по всему объему тела.

z

dmv

h

ω

y

x

Рисунок 26

Рассмотрим, как связаны кинематические характеристики вращающегося тела и его момент количества движения. Пусть твердое тело вращается с угловой скоростью вокруг неподвижной оси Оz (рис. 26). Выделим в теле бесконечно малый элемент массой

dm, находящийся на расстоянии h от оси вращения: h = 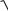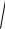x2 y2 , где

х и у – координаты выделенного элемента. Траекторией его движения является окружность с центром на оси вращения. Скорость движения элемента направлена по касательной к траектории, а ее величина равна h. Так что вектор количества движения направлен также по

касательной к траектории, и величина его равна dm x2 y2 .

72

Момент количества движения выделенного элемента относительно оси Оz равен его моменту количества движения относительно любой точки на этой оси (так же как в случае момента силы относительно оси). В качестве такой точки возьмем точку пересечения оси Оz и плоскости движения рассматриваемого элемента (рис. 26). Тогда плечом вектора количества движения служит величина h, а момент количества движения равен:

dLz dm h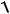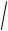x2 y2 dm x2 y2 .

Момент количества движения всего тела получим путем интегрирования этого выражения по его объему:

Здесь использовано соотношение (4.25) для момента инерции твердого тела. Таким образом, кинетический момент вращающегося тела равен произведению угловой скорости вращения на момент инерции тела относительно оси вращения.

Нетрудно увидеть аналогию между количественными характеристиками поступательного и вращательного движения. При поступательном движении количество движения механической системы определяется по формуле: К = m VC. При вращательном движении аналогом этой формулы служит соотношение (4.28): Lz = Jzω. Следовательно, кинетический момент Lz является аналогом количества движения К, т. е. служит мерой вращательного движения. При этом мерой инерционности является момент инерции Jz.

Выясним, что может быть причиной изменения момента количества движения. Сначала рассмотрим движение одной материальной точки. Оно подчиняется уравнению (4.1): m W = F, где F – равнодействующая всех сил, действующих на точку. Умножим векторно левую и правую части уравнения движения на радиус-вектор точки относительно некоторого центра О:

Справа от знака равенства стоит момент силы относительно точки О: MO(F) = r F. Левая часть равенства может быть преобразована следующим образом:

73

Здесь использованы свойства производной и векторного

Следовательно, векторно перемножаются два параллельных вектора. Такое произведение, как известно из курса математики, равно нулю. Произведение r mV, согласно (4.26), представляет собой момент количества движения материальной точки МО(mV) относительно центра О. В результате из предыдущего вытекает уравнение:

которое показывает, что причиной изменения момента количества движения материальной точки является вращательный эффект действующих на нее сил. Уравнение (4.30) устанавливает количественную сторону этой связи.

В механической системе, состоящей из N точек, для каждой из них можно составить уравнение (4.30):

Просуммируем левые и правые части всех этих уравнений. Сумма левых частей, согласно (4.27), может быть представлена в виде:

В правой части в результате суммирования уравнений получим сумму моментов всех сил (главный момент), действующих на точки механической системы. При этом сумма слагаемых, включающих внутренние силы, будет равна нулю. Действительно, каждой силе, действующей внутри механической системы, соответствует равная по величине и противоположная по направлению сила (аксиома 3). Поэтому моменты этих двух сил будут уравновешивать друг друга. В итоге получаем уравнение:

Полученное уравнение представляет собой символьную запись

теоремы об изменении кинетического момента: производная по времени от кинетического момента механической системы относительно некоторой точки равна главному моменту внешних

74

сил, действующих на точки системы, относительно той же точки.

Сформулированная теорема является основной при изучении вращательного движения твердых тел.

Для вращающегося вокруг оси Оz тела, согласно (4.28), кинетический момент равен: Lz = Jz . Если во время вращения форма тела не меняется, то момент инерции Jz = const, и уравнение (4.31) в этом случае примет вид:

Полученное уравнение называется дифференциальным уравнением вращательного движения твердого тела. В его правой части суммирование ведется по всем силам, действующим на тело.

Используя обозначение для углового ускорения dd , предыдущее

уравнение можно записать в форме аналогичной уравнению (4.17), описывающему поступательное движение твердого тела:

Jz Mz (Fj ) . j

4.8. Дифференциальные уравнения плоского движения твердого тела

Из кинематики известно (подраздел 3.4.), что плоскопараллельное движение твердого тела представляет собой наложение поступательного и вращательного движений. Оно полностью описывается тремя уравнениями (3.31), два из которых задают движение полюса, а третье характеризует вращение тела вокруг полюса. В динамике при составлении уравнений плоского движения в качестве полюса всегда выбирается центр масс тела С. Такой выбор объясняется тем, что центр масс является единственной подвижной точкой, для которой теорема об изменении кинетического момента (4.31) имеет такой же вид, как и для неподвижной точки.

При выбранном полюсе поступательная часть движения подчиняется векторному уравнению (4.17), которое в проекциях на оси декартовой системы координат равносильно двум скалярным уравнениям:

75

Здесь Fjx и Fjy – проекции на координатные оси внешних сил, действующих на тело, хС и уС – координаты центра масс (в поле сил тяжести – центра тяжести) тела.

Вращательная часть движения тела подчиняется векторному уравнению (4.31), проектируя которое на ось Оz, перпендикулярную плоскости движения тела и проходящую через его центр масс получим:

Здесь моменты инерции и моменты внешних сил вычисляются относительно оси Оz.

Уравнения (4.33) и (4.34) называются дифференциальными уравнениями плоскопараллельного движения твердого тела.

4.9. Работа и мощность механических сил

Эффект действия сил на механические системы не ограничивается изменением их количества движения или кинетического момента. Другие характеристики сил – мощность и работа. Мощность силы N при ее действии на механическую систему определяется скалярным произведением силы на скорость точки ее приложения:

Если известны проекции силы и скорости на оси декартовой системы координат, то выражение для мощности силы можно представить в виде:

Здесь x, y и z – координаты точки приложения силы.

Из предыдущих выражений следует, что мощность силы положительна, если угол между вектором силы и скорости острый. В этом случае сила оказывает разгоняющий эффект на твердое тело. Наоборот, если угол между силой и скоростью тупой, то сила оказывает на тело замедляющее воздействие, и мощность силы отрицательна. Наконец, если сила перпендикулярна направлению скорости, то мощность силы равна нулю. Сила не имеет мощности и тогда, когда она приложена к неподвижной точке (V = 0). Размерностью мощностью, как это следует из ее определения,

76

является ватт: Н м / с = Вт. Мощность является характеристикой силы в текущий момент времени.

Работа в отличие от мощности представляет собой интегральную характеристику силы, определяющую ее воздействие на тело в течение некоторого промежутка времени. Работой силы А за промежуток времени от 1 до 2 называется величина:

Если мощность в течение указанного промежутка времени остается постоянной, то работа силы равна произведению мощности на величину промежутка времени: А = N ( 2 - 1). Отсюда следует, что единицей измерения работы является джоуль: Вт с = Н м = Дж. Работа, как и мощность, может принимать положительные, отрицательные, а также нулевые значения.

Рассмотрим бесконечно малый промежуток времени d . За этот промежуток сила совершит работу, равную dA = N d . Используя соотношение (4.35) можем записать: dA = F V d . Заменим теперь вектор скорости с помощью соотношения (3.6). Тогда для элементарной работы dA получим выражение dA = F dr . Величина работы за промежуток времени от 1 до 2 может быть получена с помощью интегрирования элементарной работы:

Здесь r1 и r2 – радиусы-векторы точки приложения силы в моменты времени 1 и 2 соответственно.

Выражение (4.38) для вычисления величины работы удобно использовать тогда, когда характер движения тела не известен, и мощность силы в каждый момент времени не может быть подсчитана. При этом зависимость силы F от положения точки, к которой она приложена должна быть задана. В частности, если сила постоянна, а движение тела происходит по прямой, то работа определяется по

77

Рассмотрим несколько примеров вычисления работы сил, которые часто встречаются при функционировании технологического оборудования.

Работа силы тяжести. Пусть тело массой m перемещается в поле силы тяжести. При этом на него действует направленная вертикально вниз постоянная по величине сила равная mg (g – ускорение свободного падения). Если r1 и r2 – радиусы-векторы, характеризующие положение центра тяжести тела в начальном и в конечном положении, то из соотношения (4.38) следует:

Вектор (r2 – r1) соединяет начальное и конечное положение центра тяжести тела (рис. 27). Скалярное произведение этого вектора на вектор ускорения свободного падения g равно перепаду высот h между начальным и конечным положением тела. Поэтому величина работы силы тяжести может быть представлена в виде:

r2

r2 -r1

g

Рисунок 27

Знак «+» в полученном выражении (работа положительна) берется тогда, когда угол между векторами (r2 – r1) и g острый, т. е. тело под действием силы тяжести движется вниз. Работа отрицательна (в выражении (4.40) выбирается знак «-»), если тело движется вверх, преодолевая действие силы тяжести.

Работа сил во вращательном движении. Пусть сила F действует на твердое тело, которое вращается вокруг оси Оz с угловой скоростью . Вектор скорости V точки приложения силы направлен по касательной к траектории в сторону движения точки, а по величине он равен h, где на сей раз h – расстояние от точки приложения силы до оси вращения. В определении мощности (4.35) произведение F cos

78

(F,ˆ V) есть не что иное, как проекция силы F на направление касательной Fm. Следовательно, величину мощности при вращательном движении определяет только касательная составляющая силы. При этом мощность равна: N = Fm h. Но произведение Fm h равно моменту силы F относительно оси Оz. Поэтому мощность может быть вычислена с помощью формулы:

Знак в этом выражении выбирается в зависимости от того, является ли сила разгоняющей или замедляющей.

Если на тело действует не одиночная сила, а пара сил с моментом М, то выражение (4.41) сохранит свой вид, только вместо момента силы Mz(F) следует подставить момент пары М.

По известной мощности работу силы за промежуток времени от 1 до 2 можно найти по формуле (4.37):

т. е. работа крутящего момента равна произведению его величины на угол поворота. Знак выбирается из тех же соображений, что и в соотношении (4.41).

Работа силы упругости. Как уже отмечалось, сила упругости пропорциональна расстоянию х до некоторой фиксированной точки О (обычно она соответствует положению упругого элемента в недеформированном состоянии): F = - cx. Пусть в момент времени 1 упругий элемент занимал положение х1, а в момент времени 2 – положение х2. Воспользуемся формулой (4.38). В рассматриваемом случае она примет вид:

Таким образом, работа силы упругости пропорциональна коэффициенту жесткости и разности квадратов координат начального

79

и конечного положения упругого элемента. Если упругий элемент удаляется от нейтрального недеформированного положения ( х2х1 ), то работа силы упругости отрицательна. В противном случае – положительна.

4.10. Кинетическая энергия материальной точки и механической системы

Понятие механической энергии является одним из центральных понятий механики. Из курса физики известно, что энергия может существовать в различных видах. Для движущихся механических систем основной вид энергии – кинетическая энергия.

Кинетическая энергия Т материальной точки, обладающей массой m и скоростью V, равна:

Кинетическая энергия механической системы, состоящей из N

материальных точек, равна сумме их кинетических энергий:

Из определения кинетической энергии следует, что ее размерностью является джоуль: кг м2 /с2 = Н м = Дж. Однако, в отличие от работы кинетическая энергия не может быть отрицательной.

Для твердых тел последнюю сумму следует заменить интегрированием по всему объему тела D:

Здесь - плотность (масса единицы объема) вещества, из которого состоит твердое тело.

Приведенные общие формулы для расчета кинетической энергии существенно упрощаются для типовых видов движения твердого тела. Так, при поступательном движении, как известно из кинематики, все точки тела обладают одинаковой скоростью. Поэтому функция, стоящая под знаком интеграла в (4.47), постоянна и может быть вынесена за знак интегрирования. Оставшийся интеграл равен объему тела. Следовательно, величина кинетической энергии при поступательном движении тела может быть рассчитана по формуле:

80