MEHANIKA

многоугольник сил и многоугольник моментов сил при равновесии свободного твердого тела должны быть замкнутыми.

В проекциях на оси декартовой системы координат равенства (2.16) дадут шесть соотношений вида:

В силу произвольности выбора системы координат эти соотношения означают, что в случае равновесия свободного твердого тела алгебраическая сумма проекций всех сил, действующих на него, на три взаимно перпендикулярные оси равна нулю (первые три равенства), а также алгебраическая сумма моментов всех сил относительно этих же осей равна нулю (другие три равенства).

2.8. Силы трения

Силы трения – одни из самых распространенных сил в природе и технике. При работе машин и механизмов их, как правило, нельзя не учитывать. Они могут играть положительную роль (например, во фрикционных передачах), но чаще всего их влияние носит отрицательный характер и связано с потерями полезной энергии.

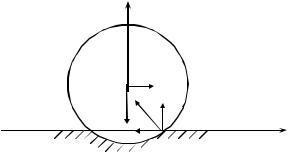
Различают трение скольжения и трение качения, природа которых различна. Трение скольжения проявляется в виде

равна сдвигающей силе Р по величине и противоположна ей по направлению. При увеличении сдвигающей силы будет увеличиваться и сила трения. Однако при достижении силой Р некоторого значения равновесие тела нарушится, и начнется его скольжение по поверхности.

В момент нарушения равновесия сила трения Fтр будет иметь наибольшее значение, которое называется силой трения покоя. Опыт показывает, что она пропорциональна нормальной составляющей N опорной реакции:

31

Коэффициент пропорциональности f называется коэффициентом трения скольжения. Его величина зависит от степени шероховатости контактирующих поверхностей, от материалов тела и поверхности, а также от физических свойств соприкасающихся тел. В каждом конкретном случае он определяется экспериментально.

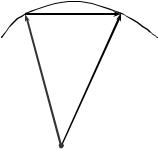
Трение качения проявляется в виде сопротивления перекатыванию

Опорная поверхность под действием веса цилиндра деформируется (на рисунке деформации показаны в сильно преувеличенном виде). Реакция опорной поверхности смещается на некоторое расстояние а от вертикали, проходящей через центр цилиндра. Вертикальная составляющая реакции равна весу цилиндра G, а горизонтальная составляющая – величине перекатывающей силы Р. Таким образом, цилиндр находится в равновесии под действие двух пар.

Уравнение равновесия, составленное при максимальном значении перекатывающей силы Рmax (на пороге равновесия), позволяет для

где R – радиус цилиндра. Если Р Рmax , цилиндр остается неподвижным. При Р Рmax цилиндр начнет движение. Величину а смещения в сторону движения точки приложения реакции называют плечом силы трения качения или коэффициентом трения качения. Она зависит от упругих свойств материалов перекатывающихся тел, прижимающей силы (в рассмотренном случае веса цилиндра), относительной угловой скорости тел.

Безразмерная величина а / R в соотношении (2.19), как правило, значительно меньше коэффициента трения скольжения f в (2.18). Поэтому в технических устройствах для уменьшения сопротивления и снижения потерь энергии на трение стремятся заменить трение

32

скольжения трением качения с помощью подшипников, катков, колес, роликов и т. д.

2.9.Контрольные вопросы

1.Какие системы сил называются эквивалентными?

2.Что такое равнодействующая системы сил?

3.Какие системы сил называются уравновешенными?

4.В чем состоят основные задачи статики?

5.В чем различие между внешними и внутренними силами, действующими на точки механической системы?

6.Сформулируйте основные аксиомы статики.

7.В чем состоит принцип отвердевания?

8.Какие силы называются активными, а какие пассивными?

9.Перечислите типы связей. Какие реакции они вызывают?

10.В чем различие связей, моделируемых гладкой поверхностью и шарнирно-подвижной опорой?

11.Какие силы называются сходящимися?

12.Как строится силовой многоугольник?

13.Сформулируйте условия уравновешенности плоской системы сходящихся сил.

14.Что такое момент силы относительно точки?

15.Что такое момент силы относительно оси?

16.Сформулируйте теорему Вариньона для плоской системы сил.

17.Что такое главный вектор и главный момент системы сил?

18.Чему равна равнодействующая параллельных сил и как найти ее линию действия?

19.Сформулируйте условия равновесия пространственной системы

сил.

20.Что такое пара сил и какое воздействие на твердые тела она оказывает?

21.Почему момент пары сил является свободным вектором?

22.Как найти пару сил, эквивалентную системе пар?

23.Чем отличается трение скольжения от трения качения? Какова физическая природа того и другого?

24.Что такое коэффициент трения скольжения и от чего он зависит?

25.Что такое коэффициент трения качения? От каких факторов зависит его величина?

33

3. КИНЕМАТИКА

Как уже отмечалось во введении, один из разделов механики изучает количественные характеристики различных типов движения материальных тел, отвлекаясь от причин, вызвавших это движение. Этот раздел называется кинематикой. Здесь также реализуется принцип «от простого к сложному». Сначала рассматриваются кинематические характеристики точки, затем простейшие виды движения твердого тела и, наконец, сложное движение точки. В заключение даются общие понятия о сферическом движении и движении свободного твердого тела.

3.1 Способы задания движения точки

При движении тела все его точки совершают определенные перемещения в пространстве. Поэтому анализ движения тела целесообразно начать с изучения движения отдельной точки. Задать движение точки означает указать такой способ, с помощью которого можно точно указать ее положение в любой момент времени в некоторой заранее выбранной системе координат. Существует три способа задания движения точки: векторный, координатный и естественный.

При векторном способе задания движения положение точки М в

пространстве задается радиус-вектором r , начало которого в любой момент времени совпадает с началом системы координат, а конец – с точкой М. Таким образом, векторное уравнение

однозначно определяет местоположение точки М в произвольный момент времени. С течением времени конец вектора r ( ) описывает в пространстве некоторую непрерывную линию, которая называется

траекторией точки М. Следовательно, траектория представляет собой геометрическое место точек пространства, через которые последовательно проходит точка М.

При координатном способе задания движения положение точки

М определяется тремя координатами (например, декартовыми), которые, также как и радиус-вектор r ( ), являются функциями времени:

34

Нетрудно видеть, что способы задания движения точки (3.1) и (3.2) связаны между собой, поскольку проекциями радиус-вектора на оси координат являются координаты конца вектора r:

где i, j, k – единичные орты декартовой системы координат.

Естественный способ задания движения точки используется тогда, когда траектория ее движения заранее известна. В этом случае на траектории выбирается некоторая фиксированная точка О (начало отсчета) и положительное направление от точки О вдоль траектории. Тогда положение точки М будет однозначно определено длиной дуги s по траектории от начала отсчета О – дуговой координатой. Ее величина при движении точки М будет функцией времени:

Следует различать величину пройденного пути от значения дуговой координаты. Разница между этими понятиями очевидна, например, при движении точки по замкнутой кривой.

3.2. Скорость и ускорение движущейся точки

Основными кинематическими характеристиками движения являются скорость и ускорение. При различных способах задания движения они вычисляются по разному.

По своему физическому смыслу скорость является мерой изменения во времени положения точки. Пусть точка М движется по криволинейной траектории (рис. 13), а ее положение в моменты времени и 1 определяется радиусвекторами r и r1.

М М1

r

r r1

О

Рисунок 13

Изменение положения точки М за промежуток времени = 1 - характеризуется вектором r. Отношение Vср = r / представляет

35

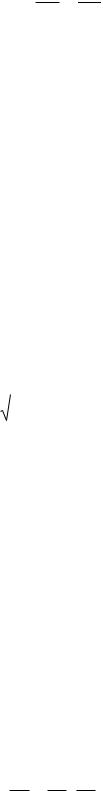
собой среднюю за промежуток скорость точки М. Очевидно, что вектор Vср направлен по секущей ММ1. В пределе при 0 точка М1 будет неограниченно приближаться к точке М, секущая ММ1 займет положение касательной к траектории в точке М, а вектор Vср будет равен мгновенному значению скорости точки V в момент времени :

Таким образом, скорость точки в данный момент времени при векторном способе задания ее движения равна производной от радиус-вектора по времени и направлена по касательной к траектории движения.

Для того чтобы получить скорость точки при координатном способе задания движения воспользуемся соотношением (3.3). Дифференцирование его по времени в соответствии с (3.5) для скорости точки М дает:

Следовательно, проекции вектора скорости точки на координатные оси могут быть получены путем дифференцирования зависимостей (3.2) по времени. Тогда модуль вектора скорости равен:

а его направление задается углами, которые образует вектор скорости с осями координат. Косинусы этих углов (направляющие косинусы) определяются с помощью формул:

При естественном способе задания движения точки каждому значению дуговой координаты s соответствует определенное положение радиус-вектора r. Другими словами, радиус-вектор точки является функцией дуговой координаты, которая, в свою очередь, согласно (3.4), зависит от времени. Это значит, что векторная величина r может рассматриваться как сложная функция : r = r(s( )). Правила дифференцирования сложной функции позволяют записать:

Vdr dr ds d ds d

36

С помощью рис. 13 нетрудно понять, чему равен первый сомножитель, который является пределом отношения r / s. В этом отношении знаменатель представляет собой длину дуги от точки М до точки М1. Когда последняя неограниченно приближается к точке М, длина дугиs неограниченно приближается к длине вектора r. Следовательно, в пределе получится единичный вектор, который, как отмечалось выше, направлен вдоль касательной к траектории движения в точке М. Обозначим единичный вектор касательной через m. Тогда на основании предыдущего равенства справедливо соотношение:

Из полученного соотношения следует, что при естественном способе задания движения модуль скорости V равен производной от дуговой координаты по времени, а вектор V направлен по касательной в сторону движения точки.

Мерой изменения во времени величины и направления скорости служит ускорение точки. Следовательно, при векторном способе задания движения ускорение W определяется равенством:

С учетом (3.3) и (3.6) проекции ускорения на оси декартовой системы координат вычисляются по формулам:

Модуль вектора ускорения и его направление можно найти с помощью соотношений, аналогичных (3.7) и (3.8):

Предыдущие соотношения позволяют вычислить ускорение точки при векторном и координатном способах задания ее движения. При естественном способе скорость определяется выражением (3.9). Тогда для ускорения можно записать:

37

Здесь учтено, что при движении точки по криволинейной траектории с течением времени меняются оба сомножителя в скобках. Производная dm / d характеризует скорость изменения направления единичного вектора касательной m, проведенной к траектории в точке М при ее движении, т. е. при изменении дуговой координаты s. Ее можно записать в виде:

dm dm ds dmV d ds d ds

В дифференциальной геометрии доказывается, что вектор dm /ds направлен вдоль внутренней нормали n к кривой, а его длина обратно пропорциональна локальному радиусу кривизны кривой в данной точке. С учетом сказанного равенство (3.14) примет вид:

Следовательно, при естественном способе задания движения точки ее ускорение может быть найдено как сумма двух векторов. Один вектор Wm направлен вдоль касательной m к траектории движения (рис. 14), его величина определяется быстротой изменения модуля

Wm

m

M

n

Wn W

Рисунок 14

скорости точки М:

Вектор Wm называется касательным ускорением. Касательное ускорение существует при неравномерном криволинейном движении, направлено по касательной к траектории при ускоренном движении (в

38

сторону положительного отсчета дуговой координаты) и в обратном направлении – при замедленном.

Другой вектор Wn направлен по нормали n к траектории в сторону ее вогнутости (рис. 14), его величина определяется быстротой изменения направления скорости движения точки. Вектор Wn называется нормальным ускорением. Величина нормального ускорения всегда положительна и равна:

Модуль полного ускорения W может быть найден через величины касательного и нормального ускорений:

Соотношения (3.16) и (3.17) позволяют проанализировать некоторые частные случаи движения точки. Так, если траекторией движения точки служит прямая линия, то радиус кривизны ρ = ∞, и нормальное ускорение, согласно (3.17), равно нулю. В этом случае полное ускорение совпадает с касательным. При этом если направления векторов скорости и ускорения совпадают, то движение точки ускоренное, если их направления противоположны, то – замедленное.

При равномерном движении модуль скорости точки V dds = const.

Поэтому, согласно (3.16) касательное ускорение равно нулю, и полное ускорение совпадает с нормальным. Интегрирование последнего равенства позволяет получить уравнение равномерного движения:

которое определяет величину дуговой координаты в любой момент времени. Объединяя оба рассмотренных случая, приходим к равномерному прямолинейному движению, при котором и касательное, и нормальное ускорения отсутствуют.

Наконец, при равнопеременном движении точки величина ее касательного ускорения постоянна: Wm = const. Дважды интегрируя соотношение (3.16) можно получить закон изменения скорости и дуговой координаты при этом типе движения:

39

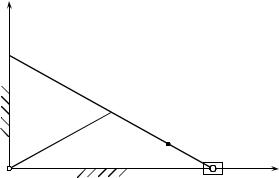
В качестве примера использования приведенных соотношений рассмотрим следующую задачу. При работе механизма, изображенного на рис. 15, кривошип ОС равномерно вращается вокруг шарнира О. Ползуны В и D перемещаются по направляющим, роль которых на рисунке выполняют оси координат Ох и Оy. На шатуне ВD находится точка М, совершающая в плоскости Охy движение, заданное уравнениями:

Требуется найти траекторию движения точки М, ее скорость и ускорение в те моменты времени, когда она пересекает ось Оy.

y

В

C

М D

Рисунок 15

Для нахождения траектории исключим время из уравнений движения точки М. Разделим первое уравнение на а, второе уравнение - на b и воспользуемся тригонометрическим тождеством: sin2 + cos2 = 1. В результате получим соотношение, связывающее координаты точки М в произвольный момент времени:

Полученное уравнение, как известно, является уравнением эллипса с полуосями а и b и с центром в начале координат. Таким образом, траекторией любой точки на шатуне служат эллипсы. Поэтому механизм, изображенный на рис. 15, называется эллипсограф.

Найдем моменты времени, когда точка М пересекает ось Оу. Для точек на этой оси х = 0. Приравнивая первое уравнение движения к нулю, получаем: i = ( / 2 + i) / k.

Проекции скорости на координатные оси определим, дифференцируя уравнения движения точки М по времени:

40