
MEHANIKA
.pdf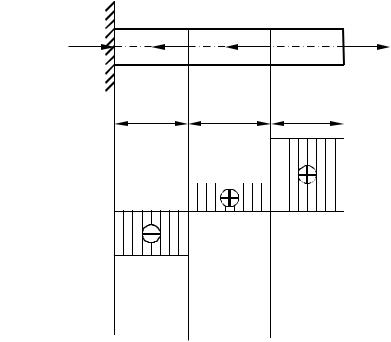
Таблица исходных данных
Номер |
м |
м |
м |
|
|
|
м |
м |
м |
|
|
|
|
строки |
|
|
|
|
|
|
|||||||
, кН/ |
, кН/ |
, кН/ |
, кН |
, кН |
, кН |
, кН |
, кН |
, кН |
м |
м |
м |
||
|
|||||||||||||
|
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
|
|
q |
q |
q |
F |
F |
F |
M |
M |
M |
, |
, |
, |
|
|
l |
l |
l |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
40 |
30 |
20 |
10 |
30 |
20 |
20 |
40 |
60 |
4 |
2 |
4 |
|
1 |
20 |
10 |
30 |
40 |
20 |
30 |
30 |
50 |
20 |
1 |
2 |
1 |
|
2 |
20 |
30 |
20 |
40 |
30 |
20 |
30 |
50 |
10 |
3 |
4 |
2 |
|
3 |
40 |
20 |
20 |
60 |
50 |
30 |
20 |
40 |
30 |
3 |
5 |
3 |
|
4 |
30 |
40 |
20 |
50 |
30 |
60 |
20 |
50 |
10 |
2 |
4 |
2 |
|
5 |
30 |
50 |
20 |
20 |
40 |
60 |
40 |
20 |
40 |
2 |
4 |
1 |
|
6 |
30 |
50 |
40 |
40 |
20 |
40 |
20 |
20 |
40 |
2 |
5 |
2 |
|
7 |
30 |
50 |
10 |
60 |
40 |
20 |
40 |
20 |
20 |
2 |
5 |
1 |
|
8 |
30 |
50 |
5 |
60 |
20 |
60 |
20 |
40 |
20 |
2 |
4 |
2 |
|
9 |
30 |
50 |
20 |
40 |
20 |
60 |
10 |
20 |
40 |
2 |
5 |
2 |
Пример решения
Задача 1. Определим величину продольной силы на каждом грузовом участке прямолинейного стержня, нагруженного системой внешних сил, линии действия которых совпадают с осью стержня (см. рис.). Затем по полученным результатам построим эпюру продольной силы.
Исходные данные. F1 = 40 kH; F2 = 30 kH; F3 = 40 kH. Направления сил и сечения их приложения указаны на рисунке.
|
F =40 kH |
F2=30 kH |
|
R=30 kH |
3 |
|
F1=40 kH |
|
|
+
I II III
ℓ1 = 1м ℓ2 = 2м ℓ3 = 1м
40
10 
N, kH
30
261
Решение. Проектируя внешние силы на ось стержня, найдем реакцию R в опоре:
R + F1 – F2 – F3 = 0; R = 40 + 30 – 40 = 30 kH.
Проведем сечение I-I в пределах I грузового участка и мысленно отбросим правую часть стержня. Направим вектор искомой продольной силы N вдоль внешней нормали к сечению (см. рис.). Составим уравнение равновесия для рассматриваемой части стержня, из которого определим величину продольной силы на первом
грузовом участке:
I
R + N = 0; N = - R = - 30 kH. |
|
R=30 kH |
N |
|
|
|
|
||
|
|
|
|
|
Знак минус означает, что истинное |
|
|
||
направление |
продольной |
силы |
|
I |
противоположно |
выбранному (см. |
рис.). |
|
|
Следовательно, вектор N направлен вдоль внутренней нормали к сечению, и материал в пределах первого грузового участка испытывает сжатие силой 30 кН. Поскольку сечение I-I проведено в произвольном месте первого грузового участка, а значение N не зависит от координаты сечения, то во всех сечениях этого грузового участка продольная сила одинакова, равна 30 кН, направлена по внутренней нормали и вызывает деформацию сжатия материала.
Аналогично получим значения N на втором и третьем грузовых участках. Для второго участка
N + R – F = 0; N = 40 – 30 =10 kH. |
F3=40 kH II |
|||||
|
3 |
|
|
R=30 kH |
|
|
|
|
|
|
|
||
Следовательно, во всех сечениях |
|
|||||
второго грузового участка продольная |
II |
|||||
сила направлена |
вдоль |
внешней |
||||
нормали, равна 10 кН и вызывает |
|
|||||
деформацию растяжения. Для третьего участка |
|
|||||
N + R – F2 – F3 = 0; N = 30 + 40 – 30 = 40 kH. |
|
|||||
Следовательно, |
во |
всех |
|
F2=30 kH |
||
сечениях |
третьего |
грузового |
R=30 kH |
|||
|
||||||
участка |
продольная |
сила |
|
|||
направлена |
вдоль |
внешней |
|
|
||
нормали к сечению, равна 40 кН |
F3=40 kH |
|||
и |
вызывает |
деформацию |
||
|
||||
растяжения.
N
III
N
 III
III
262
Полученные результаты представляются в виде эпюры. Она строится непосредственно под расчетной схемой. Рядом указывается, для какой величины построена эпюра и в каких единицах измеряется эта величина. Выше нулевой линии откладываются положительные значения, ниже – отрицательные значения.
В данной задаче зависимость силы N от продольной координаты носит ступенчатый характер. Из эпюры видно, что наибольшие растягивающие усилия возникают на третьем грузовом участке, тогда как на первом участке материал испытывает наибольшие сжимающие усилия.
Ответ. Роль итогового ответа по задаче играет построенная эпюра.
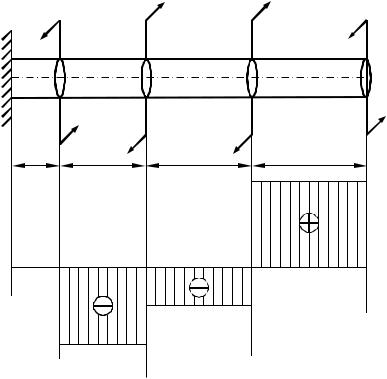
Задача 2. Определим величину крутящего момента на каждом грузовом участке стержня, нагруженного системой скручивающих моментов (см. рис.). Затем по результатам решения построим эпюру крутящего момента Т.
T4=40 кНм T3=20 кНм T2=80 кНм T1=60 кНм
T0=0 кНм |
|
|
|
|
|
|
I |
|
II |
|
III |
|
IV |
ℓ1=1м ℓ2=2м |
|
ℓ3=3м |
|
ℓ4=3м |
||
60
T, кНм
20
40
Решение. Последовательность решения этой задачи точно такая же, как и предыдущей. Прежде всего, найдем реактивный момент в заделке Т0, составив уравнение равновесия для всего стержня:
Т0 + Т1 + Т4 – Т2 – Т3 = 0; Т0 = 80 + 20 – 60 – 40 = 0 кН∙м.
Проведем сечение I-I в пределах I грузового участка и мысленно отбросим правую часть стержня. Направим искомый крутящий момент
263

Т в положительном направлении, т. е. |
|
|
I |
||
так чтобы он вращал сечение против |
|
|
|||
|
|
Т |
|||
часовой стрелки, если смотреть со |
|
|
|||
|
|
|
|||
стороны внешней нормали к сечению |
|
|
|
||
(см. рис.). |
Составим уравнение |
Т0 |
= 0 |
n |
|
равновесия |
для оставшейся части |
||||
|
|
|
|||
стержня, из которого определим |
|
величину крутящего момента на |
|
первом грузовом участке: |
I |
|
|
Т0 + Т =0; Т = - Т0 = 0 кН∙м. |
|
Таким образом, на первом грузовом участке материал кручения не испытывает.
Найдем величину крутящего момента на втором грузовом участке. Для этого мысленно проведем в произвольном сечении этого участка
сечение II-II и отбросим правую |
|
|
II |
|||
часть |
стержня |
как |
более |
|
Т4 |
|
нагруженную. Составляя уравнение |
|
Т |
||||
равновесия для этой части стержня, |
|
|
||||
|
|
|
||||
получим значение момента Т на |
|
|
|
|||
втором грузовом участке: |
Т0 |
= 0 |
|
n |
||
|
|
|
|
|||
Т + Т0 + Т4 = 0;
Т = - 40 – 0 = - 40 кН∙м
II
Знак минус показывает, что истинное направление крутящего момента противоположно выбранному (см. рис.).
Совершенно аналогично найдем, что значение крутящего момента на третьем грузовом участке равно – 20 кН∙м, а на четвертом грузовом участке 60 кН∙м.
По полученным результатам непосредственно под расчетной схемой строим эпюру крутящего момента, которая является ступенчатой, поскольку в пределах каждого грузового участка момент постоянен. Из эпюры видно, что наибольшие внутренние усилия возникают на участке IV, где крутящий момент имеет максимальное значение (60 кН∙м).
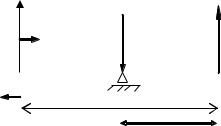
Задача 3. Определим зависимость поперечной силы и изгибающего момента от продольной координаты для балки, расчетная схема которой приведена ниже. Затем полученные зависимости представим в виде соответствующих эпюр.
264
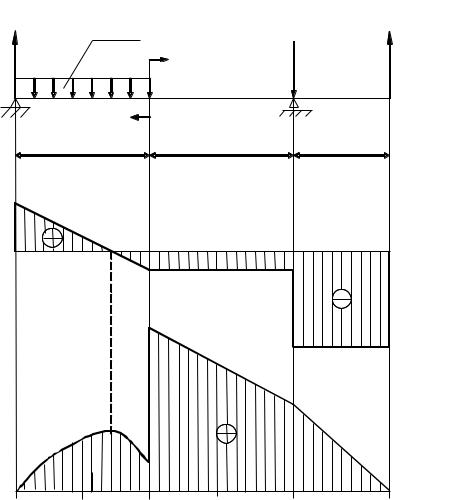
YA=28kH |
q=20kH/м |
YВ=60kH |
F=72kH |
||
|
|
||||
|
|
М=80kHм |
|
|
|
I |
|
|
II |
|
III |
|
l1=2м |
l2=2м |
|
l3=1м |
|
28 |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
Qx, kH |
|
|
12 |
|
|
|
|
|
96 |
|
|
|
|
|
|
|
|
72 |
|
19,6 |
|
|
72 |
|
|
16 |
|
|
|
|
|
|
|
|
|
M , kHм |
|
|
|
|
|
, x |
Решение. Прежде всего, определим опорные реакции YA (левая |
|||||
опора) и YB (правая опора), составив уравнение равновесия балки в |
|||||
форме (2.9'): |
|
|
|
|
|
МА 0 ; - q ∙2∙ 1 – M – 4 ∙ YB + 5 ∙ F = 0; YB = 60 kH.
Знак плюс означает, что предварительно выбранное направление реакции YB (вниз) оказалось правильным.
МВ 0 ; q ∙2 ∙3 – M – 4 ∙ YA + 1 ∙ F = 0; YA = 28 kH.
Реакция в левой опоре направлена вверх.
Для того чтобы убедиться, что реакции опор найдены правильно, составим уравнение по равновесия по силам в проекциях на вертикальное направление:
YA - q ∙2 - YB + F = 28 – 40 – 60 + 72 = 0.
265

Как и должно быть, уравнение равновесия выполняется.
Проведем сечение I-I на первом грузовом участке на расстоянии х от левой опоры балки (0 ≤ x ≤ 2) и рассмотрим
ее левую часть. В сечении введем локальную систему координат так, как указывалось в
подразделе 5.2 (рис. 31, г). Именно, ось Оу направим вниз, ось Оz – «на наблюдателя». Положительные направления искомых
внутренних силовых факторов ( Qy и Mz ) совпадают с положительными направлениями осей.
Составим два уравнения равновесия действующих на рассматриваемую часть равновесия по силам:
Qy – YA + qx = 0; Qy = YA – qx = 28 – 20x (kH).
Уравнение равновесия по моментам относительно рассматриваемого сечения:
Mz + 0.5 qx2 – YAx = 0; Mz = - 0.5 qx2 + YAx = - 10x2 + 28x (kH∙м).
Полученные зависимости для поперечной силы и изгибающего момента показывают, что в данной задаче внутренние силовые факторы меняются от сечения к сечению. Поперечная сила линейно зависит от координаты х, а изгибающий момент – по параболическому закону. Графическое представление этих зависимостей приведено на эпюре непосредственно под первым грузовым участком расчетной схемы. Нетрудно подметить закономерность, связывающую эпюры поперечной силы и изгибающего момента. Там, где Qy положительна, момент Mz возрастает. Там, где Qy отрицательна, момент Mz убывает. Наконец, в тех точках, где Qy обращается в нуль, изгибающий момент достигает локального экстремума. Такая связь между эпюрами имеет место в силу того, что в каждом сечении справедливо следующее соотношение:
dM z ( x) Q ( x) , dx
которое можно использовать для самопроверки при решении данной задачи.
Найдем внутренние силовые факторы на втором грузовом участке. Проведем сечение в пределах этого участка, мысленно отбросим левую часть балки (как более нагруженную) и рассмотрим равновесие
266
оставшейся части. Здесь локальная координата х меняется от 1 до 3. Как указывалось в подразделе 5.2, теперь в сечении следует ввести правую систему координат, т. е. ось Оу направим вверх, ось Оz – «от наблюдателя». Тогда положительные направления поперечной силы и
изгибающего момента будут такими, |
|
|
|
|
|
|
|
|
||
|
|
|
Qy |
|
|
F=72kH |
||||
|
|
|
YВ=60kH |
|||||||
как показано на рисунке. Составим |
|
|
|
|||||||
|
|
|
|
|
|
|||||
уравнения |
равновесия |
для |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
оставшейся части балки. Уравнение |
Mz |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
равновесия по силам: |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
x |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Qy + F – YB = 0; Qy = YB – F = - 12 кН.
Видим, что на втором грузовом |
|
ℓ3=1м |
||
участке поперечная сила |
от |
|
|
|
координаты х не зависит. |
|
|
|
|
Уравнение |
равновесия |
по |
моментам |
относительно |
рассматриваемого сечения:
Mz + YB (x – 1) – Fx = 0; Mz = Fx – YB (x – 1) = 12x + 60 кН.
Полученные зависимости отобразим на эпюрах.
Аналогичные построения и выкладки сделаем для третьего грузового участка. В результате получим: Qy = - 72 кН; Mz = 72х кН∙м. Эти зависимости также перенесем на эпюры.
В заключение еще раз обратим внимание на связь между поперечной силой и изгибающим моментом, которая прослеживается на эпюрах по всей длине балки. Кроме того, в сечениях, где приложены сосредоточенная сила или сосредоточенный момент, соответствующая эпюра терпит скачок, величина которого в точности равна величине приложенной здесь внешней нагрузки.
Контрольная работа № 5.
Расчет на прочность и жесткость при простых видах нагружения стержня
Настоящая контрольная работа является продолжением предыдущей и основана на полученных в ней результатах. Контрольная также состоит из трех задач.
Задача 1. Для расчетной схемы первой задачи предыдущей контрольной работы из условия прочности выбрать стандартный стержень квадратного поперечного сечения при условии, что сечение постоянно на всех грузовых участках; найти величину нормальных напряжений в опасном сечении выбранного стержня и построить эпюру распределения напряжений по поперечному сечению стержня;
267
определить осевые перемещения сечений стержня и построить эпюру перемещений; проверить выполнение условия жесткости.
Если условие жесткости не выполняется, выбрать стандартный стержень новых размеров поперечного сечения.
Исходные данные. Эпюра продольной силы, построенная в предыдущей контрольной работе, допускаемое напряжение на растяжение – сжатие [σ]= 150 МПа, модуль продольной упругости Е = 2∙1011 Па, допускаемое значение удлинения стержня [Δℓ] = Σℓi∙10-4 м, где ℓi – длины грузовых участков.
Задача 2. Для расчетной схемы второй задачи предыдущей контрольной работы из условия прочности выбрать стандартный стержень круглого поперечного сечения, определить величину касательного напряжения вдоль диаметра опасного сечения и построить его эпюру, вычислить углы закручивания сечений выбранного стержня и построить эпюру углов закручивания, проверить выполнение условия жесткости.
Если условие жесткости не выполняется, определить новый стандартный диаметр стержня сплошного круглого сечения.
Исходные данные. Эпюра крутящего момента, построенная в предыдущей контрольной работе, допускаемое напряжение на кручение [τ] = 90 МПа, модуль сдвига G = 8∙1010 Па, допускаемый относительный угол закручивания [Φ]=1,2∙10-2 рад/м.
Задача 3. Для расчетной схемы третьей задачи предыдущей контрольной работы из условия прочности по нормальным напряжениям подобрать по сортаменту прокатной стали (приложение А) стандартную балку двутаврового поперечного сечения, для выбранной балки построить эпюру нормальных напряжений σ по высоте опасного сечения, где Mx=|Mxmax|, проверить прочность балки по касательным напряжениям, построить эпюру распределения касательных напряжений τ по высоте опасного сечения, в котором Qx=|Qxmax|, определить углы поворота и прогибы сечений построить их эпюры, проверить условие жесткости.
Если условие жесткости не выполняется, по сортаменту проката определить новый номер двутавра.
Исходные данные. Эпюры поперечных сил и изгибающих моментов, построенные в предыдущей контрольной работе, допускаемые нормальные и касательные напряжения при изгибе [σ] = 160 МПа, [τ] = 100 МПа, модуль продольной упругости Е = 2∙1011 Па, допускаемый прогиб балки [y] = ℓ/300 – для пролетной части балки и [y] = ℓ/100 – для консоли.
Пример решения
Задача 1. Рассмотрим расчетную схему стержня, нагруженного внешними силами, которые действуют строго вдоль его оси. Эпюра
268

продольной силы для этого случая нагружения была получена при решении примера для предыдущей контрольной работы.
|
F =40 kH |
|
F2=30 kH |
|
F0=30 kH |
3 |
|
|
F1=40 kH |
|
|
|
||
|
I |
II |
III |
|
|
ℓ1 = 1м ℓ2 = 2м ℓ3 = 1м |
|
||
|
|
|
|
40 |
10 
N, kH
30 |
5,19 |
Δℓ∙104, м
1,73
5,19
а) Для определения размеров постоянного по длине поперечного стержня квадратного сечения воспользуемся условием прочности (5.11):
max |
|
N max |
, |
|
|
A |
|
где σmax – максимальное значение нормального напряжения при растяжении – сжатии; |Nmax| – максимальное значение продольной силы, определяемое по эпюре; А – площадь поперечного сечения
стержня. В нашем случае |Nmax| = 40 кН (см. эпюру), [σ]= 150 МПа. Решая предыдущее неравенство относительно площади А, получаем:
A |
Nmax |
|
40 103 |
2,67 10 |
4 м2. |
. |
тр |
|
|
150 106 |
|
|
|
|
|
|
|
|
Поскольку по условию задачи поперечное сечение имеет форму квадрата, то сторона квадрата:
aтр 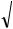 Aтр
Aтр 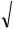 2,67 10 4 1,63 10 2 м 16,3мм.
2,67 10 4 1,63 10 2 м 16,3мм.
269

Расчетное значение стороны квадрата а округляем до ближайшего большего значения из стандартного ряда поперечных размеров стального прутка круглого и квадратного поперечного сечения: (по ГОСТ 6636-69, ряда Ra40), мм: 10; 10,5; 11; 11,5; 12; 13;
14; 15; 16; 17; 18; 19; 20; 21; 22; 24; 25; 26; 28; 30; 32; 34; 36; 38; 40; 42; 45; 48; 50; 53; 56; 60; 63; 67; 71; 75; 80; 85; 90; 95; 100; 105; 110; 120; 125; 130; 140; 150; 160; 170; 180; 190;200; 210; 220; 240; 250; 260; 280;
300 и т.д. Для нашего случая стандартное значение а = 17 мм. Тогда А
= 172 = 289 мм2 = 2,89∙10-4м2.
б) Нормальные напряжения в материале при растяжениисжатии стержней определяются по формуле (5.8):
|
|
|
N max |
|
3 |
|
Па 138МПА. |
|
|
|
|
40 10 4 1,38 10 8 |
|||||
|
|
|
A 2,89 10 |
|
|
|
||
Внешние силы действуют строго |
|
σ, МПА |
||||||
по оси |
стержня. |
Следовательно, |
|
|||||
|
|
138 |
||||||
напряжения |
в |
сечении |
будут |
|
|
|||
17 |
|
|
||||||
|
|
|||||||
распределены равномерно. |
Выбранное |
|
|
|||||
стандартное сечение стержня и эпюра |
|
|
|
|||||
возникающих |
в |
нем |
напряжений |
|
17 |
|
||
показаны на рисунке. |
|
|
|
|
|
|
||
в) |
Деформация на i |
- |
м участке |
|
|
|
||
стержня при растяжении – сжатии определяется по закону Гука (5.10), записанному для деформаций:
xi x(i 1)k |
Nxi xi |
, |
|
E A |
где Δℓx(i-1)k – перемещение крайнего сечения i - 1 грузового участка на границе с i -м участком.
Nxi – продольная сила на i - м участке;
xi – координата произвольного сечения на i-м участке относительно его начала.
Нумерацию участков при построении эпюры Δℓ рекомендуется вести от заделки стержня, так как сечение в заделке неподвижно и его перемещение всегда равно нулю.
I – й грузовой участок 0 ≤ x1 ≤ 1:
x1 0 |
0 |
30 103 0 |
|
0 , |
||
11 |
2,89 |
10 |
4 |
|||
|
2 |
10 |
|
|
||
x 1 |
0 |
30 103 |
1 |
4 |
5,19 10 4 м, |
|
1 |
2 |
11 |
2,89 |
10 |
|
|
|
10 |
|
|
|||
270
