
MEHANIKA
.pdfременная, цепная и другие механические передачи вращательного движения от двигателя к рабочему органу агрегата могут быть названы в качестве примеров механизмов.
Важную роль при работе ХТС имеют трубопроводы и трубопроводная арматура для управления материальными потоками обрабатываемых веществ (задвижки, запорные и регулирующие клапаны, пробковые и шаровые краны, затворы дисковые и т. д.).
С точки зрения особенностей конструкции и габаритов промышленному химическому оборудованию свойственно огромное разнообразие. Поэтому важным вопросом является вопрос о его рациональной классификации. В качестве основного признака для классификации машин и аппаратов целесообразно принять их функциональное (технологическое) назначение. Так, аппараты для проведения теплообменных процессов называются теплообменниками, для проведения процессов выпаривания – выпарными аппаратами, для проведения процессов сушки – сушилками и т. д.
Классификация по признаку назначения распространяется не только на машины и аппараты, но и на их крупные блоки – сборочные узлы с четким функциональным назначением. Например:
-рабочие органы машин, непосредственно взаимодействующие с обрабатываемым веществом, - колеса насосов, вентиляторов, газодувок, мешалок, валки дробилок, барабаны центрифуг и барабанных сушилок;
-прессформы для прессования деталей из пластмасс;
-корпусные (базовые) блоки машин и аппаратов;
-блоки сальниковых, торцовых, манжетных, фланцевых и других устройств для герметизации рабочего объема оборудования и трубопроводов, содержащих экологически опасные обрабатываемые среды;
-опорные устройства для аппаратов, а также для вращающихся валов, осей, барабанов в виде подшипников качения, скольжения или в виде специальных вращающихся роликов;
-электромеханические, пневматические, гидравлические приводы машин и механизмов;
-муфты для соединения рабочего ротора машины с ее приводом.
Всвою очередь сборочные узлы могут состоять из большого числа самых разнообразных деталей (деталью называется часть агрегата, которую можно изготовить без применения сборочных операций – вал, болт и т. п.).
Детали в курсе «Механика» с точки зрения анализа их работоспособности делятся на три класса в зависимости от их геометрической формы: стержни, тонкостенные оболочки и массивные твердые тела. Точные определения этих понятий будут даны ниже.
11
1.2. Технологические нагрузки и воздействия
Характер нагрузок и воздействий, которые испытывают элементы химико-технологического оборудования обусловлен условиями проведения промышленных процессов в химической, нефтехимической и смежных областях промышленности. Основной особенностью большинства таких производств является переработка огромных масс высоко-агрессивных веществ в условиях высоких температур и давлений. В результате оборудование подвергается значительным нагрузкам механической, физико-механической и химической природы.
Внешние силовые воздействия на детали и узлы во время эксплуатации оборудования непосредственно связаны с функциональным назначением этих изделий. Так, например, внешние силовые воздействия на ротор молотковой дробилки и на корпус теплообменника совершенно различны как по характеру, так и по интенсивности.
Для установления, а затем и для количественного учета наиболее важных внешних воздействий любую деталь условно рассматривают изолированно от других деталей, заменяя при этом действие мысленно отброшенных деталей (в том числе и их связей - опорных устройств) внешними силами, которые принято называть нагрузками.
По способу приложения различают нагрузки поверхностные и объемные. Непосредственное взаимодействие деталей между собою и с окружающей средой (в том числе и с обрабатываемой в оборудовании рабочей средой) происходит по некоторым поверхностям контакта, что и определило термин - поверхностная нагрузка. Величина нагрузки, действующая на единицу поверхности контакта, называется интенсивностью нагрузки или давлением. Она измеряется в Паскалях: Па = Н/м2. В качестве примеров можно указать давление рабочей среды на стенки аппаратов, ветровую нагрузку на корпус ректификационной колонны и др.
Если площадь приложения нагрузки имеет малую ширину по сравнению с длиной, то для упрощения расчетов целесообразно заменить поверхностную нагрузку распределенной по линии нагрузкой. Такая нагрузка имеет размерность Н/м и называется погонной нагрузкой. В тех случаях, когда участок действия погонной нагрузки мал по сравнению с размерами детали, ее можно рассматривать как сосредоточенную (приложенную в точке). Размерность сосредоточенной нагрузки Н.
Кроме сосредоточенных сил, детали оборудования бывают нагружены внешними сосредоточенными моментами сил,
характеризующими внешнее вращательное воздействие на деталь и имеющими размерность Н м.
12
Если внешние силы не являются результатом контактного взаимодействия двух тел, а приложены к каждой точке объема материала детали (силы собственного веса, силы инерции, центробежные силы и др.), то они называются объемными и имеют размерность Н / м3.
Детали технологического оборудования часто оказываются под воздействием тепловых нагрузок, возникающих при стесненности
свободного температурного перемещения детали. Такие перемещения возникают при нагревании или охлаждении детали до любой температуры, отличающейся от температуры сборки изделия. Кроме того, тепловые нагрузки возникают и вследствие непостоянства температуры детали по ее поверхности, толщине и т. п.
По характеру изменения во времени нагрузки бывают статические и динамические. К статическим нагрузкам относят постоянные во времени или нагрузки, изменяющиеся настолько медленно, что вызываемые ими ускорения и силы инерции пренебрежимо малы (например, снеговая нагрузка на крышку резервуара).
Динамические нагрузки бывают мгновенно приложенными (ударными, например, при столкновении двух тел) и повторнопеременными, которые изменяются во времени по тому или иному закону. Процесс динамического нагружения деталей сопровождается значительными их ускорениями и силами инерции, подлежащими обязательному учету. Практика эксплуатации показывает, что почти все современные машиностроительные материалы сопротивляются динамическим нагрузкам значительно хуже, чем статическим.
По продолжительности действия нагрузки делятся на постоянные и временные. К постоянным относят нагрузки, действующие в течение всего срока службы агрегата (например, собственный вес его деталей). Временные нагрузки действуют лишь на протяжении отдельных периодов эксплуатации или монтажа объекта (например, повышенное давление в аппарате на стадии его гидроиспытаний).
1.3. Основные допущения и расчетные схемы
Как уже отмечалось во введении, при анализе поведения детали или элемента конструкции под действием нагрузок, используется метод целесообразных упрощений. Он заключается в создании идеализированной упрощенной картины взаимодействия объекта и внешних сил, которая служит своего рода моделью реального физического явления. Такую модель часто называют расчетной схемой. В модели должны быть учтены все наиболее существенные факторы, влияющие на поведение реального объекта. Но вместе с тем модель не должна быть загромождена второстепенными
13
факторами, учет которых только неоправданно усложняет анализ и расчет изучаемого явления.
Очень важно четко представлять, в рамках каких упрощений построена модель. Целый ряд упрощений касается свойств конструкционного материала, из которого изготовлены элементы оборудования:
1.Материал в механике предполагается однородной изотропной сплошной средой, не зависящей от особенностей его микроструктуры. Однородность означает идентичность механических свойств материала в его различных объемах. Свойство изотропности предполагает неизменность этих свойств в различных направлениях. Наконец, свойство сплошности позволяет не учитывать молекулярную природу вещества и считать его равномерно «размазанным» по занятому материалом объему. Это позволяет использовать аппарат непрерывных функций при изучении напряжений и деформаций, возникающих в материале.
2.Материал деталей является идеальной упругой средой, способной восстанавливать свою первоначальную форму и размеры после снятия нагрузки. Поэтому деформации, которые полностью исчезают после снятия нагрузки, соответственно называются упругими в отличие от пластических, или остаточных, не исчезающих после разгрузки. При решении некоторых задач целесообразно считать изучаемый объект абсолютно недеформируемым (абсолютно твердым).
3.Перемещения нагруженных деталей настолько малы, что размеры деталей можно считать постоянными, а взаимное расположение нагрузок в пространстве неизменным. Это допущение позволяет пренебречь влиянием деформаций материала на распределение внешних сил.
Важные упрощения при составлении расчетной схемы вносятся в геометрию изучаемого элемента оборудования. Все многообразие форм деталей и конструкций сводится к трем типовым геометрическим формам твердого тела: стержню, тонкостенной оболочке и массиву.
Стержнем называется тело, длина которого значительно (по крайней мере, на порядок) превышает размеры поперечного сечения. Геометрическое место точек, являющихся центрами тяжести поперечных сечений, называется осью стержня. В зависимости от формы оси стержень может быть прямым, кривым или пространственно изогнутым.
14
Расчетная схема стержня используется при анализе работоспособности таких элементов оборудования как валы и оси, опорные балки и стойки, а также колонные аппараты большой высоты.
Тонкостенной оболочкой (пластиной) называется тело, одно из измерений которого (толщина) мало по сравнению с двумя другими. Условная поверхность пластины или оболочки, находящаяся на равном расстоянии от внутренней и наружной поверхности, называется срединной. По форме срединной поверхности различают сферические, конические, цилиндрические и другие типы оболочек. Расчетная схема тонкостенной оболочки используется при анализе работоспособности элементов корпусов технологических аппаратов, трубных решеток в теплообменниках, трубопроводов.
Массивом называется тело, у которого все три измерения являются
величинами одного порядка. Под расчетную схему массива подпадают, например, элементы толстостенных корпусов аппаратов высокого давления.
Реальные детали технологического оборудования с достаточной для практики точностью часто могут быть представлены в виде сочетания указанных трех моделей геометрической формы. Например, расчетную схему болта можно представить в виде сочетания длинного резьбового стержня и массивной его головки, протяженную трубу с фланцевым разъемом – как сочетание тонкостенного стержня-трубы с кольцевой пластинкой.
15
2. СТАТИКА
Разделы «Статика», «Кинематика», «Динамика» традиционно излагаются в аксиоматическом построении. Это вовсе не значит, что положения этих разделов претендуют на безусловную точность подобно математическим теоремам. Наоборот, именно здесь используются наиболее сильные абстракции, такие как материальная точка или абсолютно твердое тело. Поэтому нужно отдавать себе отчет в том, что в каждом из перечисленных разделов рассматривается лишь одна сторона многогранной картины поведения деформируемых тел под действием внешних сил.
В настоящем разделе анализируются различные виды систем сил, излагаются методы их преобразования, формулируются условия равновесия систем сил.
2.1. Основные понятия и аксиомы статики
Любое материальное тело под действием сил может находиться либо в состоянии покоя, либо совершать определенное движение. Каждое из этих состояний в механике называется кинематическим состоянием тела. Изменение кинематического состояния означает изменение характера движения тела, в том числе нарушение состояния покоя или, наоборот, его достижение.
Изменение кинематического состояния механической системы (в частности, твердого тела) происходит вследствие действия на нее сил со стороны других тел или физических полей. Поэтому силу можно рассматривать как меру механического действия одного материального тела на другое. Сила характеризуется численным значением, точкой приложения и линией действия. Следовательно, сила – величина векторная. Совокупность нескольких сил {Fi}n называется системой сил (векторные величины, в отличие от скалярных, обозначаются жирными буквами).
Две системы сил {Fi}n и {Qi}m называются эквивалентными, если при замене одной из них на другую кинематическое состояние свободного тела не изменится. Для эквивалентных систем сил используется обозначение:
{Fi}n ~ {Qi}m.
Одна сила R, эквивалентная некоторой системе сил {Fi}n,
называется ее равнодействующей:
R ~ {Fi}n .
16

Если система сил {Fi}n эквивалентна нулевой силе, то она называется уравновешенной. Уравновешенная система сил не меняет кинематического состояния тела. В частности, если оно находилось в состоянии равновесия, то после приложения уравновешенной системы сил состояние равновесия не будет нарушено.
Основные задачи статики как раздела механики состоят в изложении методов преобразования одних систем сил в другие, им эквивалентные, а также в установлении условий, которым должны удовлетворять системы сил, чтобы они были уравновешенными. Указанные условия можно рассматривать как условия равновесия материального тела, если до приложения к нему сил оно находилось в состоянии покоя.
Все силы по отношению к данной механической системе делятся на внешние и внутренние. Внешними называются силы, которые действуют на точки данной механической системы со стороны тел или точек, не входящих в эту систему. Внутренними силами называются силы взаимодействия точек самой системы.
Основные положения статики выводятся из нескольких простых и наглядных аксиом, справедливость которых подтверждена опытом.
Аксиома 1. Система из двух сил, действующих на тело, является уравновешенной в том случае, если эти силы имеют общую линию действия, равны по величине и направлены в противоположные стороны.
F1 A B F2
Рисунок 1
Используя ранее введенное обозначение, для системы сил, изображенной на рис. 1, можно написать:
{F1, F2} ~ 0, если F1 = F2.
Из первой аксиомы следует, что система из одиночной силы не может быть уравновешенной.
Аксиома 2. Две системы сил, отличающиеся друг от друга на уравновешенную систему сил, эквивалентны.
Согласно этой аксиоме действие любой системы сил на твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил.
17

Аксиома 3. Система двух сил, приложенных в одной точке, имеет равнодействующую, равную их векторной сумме и приложенную в той же точке.
Из векторной алгебры известно, что сумма двух векторов может быть представлена диагональю параллелограмма, построенного на этих векторах как на его сторонах. Следовательно, равнодействующая R двух сил F1 и F2 может быть получена с помощью несложного построения (рис.2), а ее величина по теореме косинусов равна:
R F2 |
F2 |
2FF cosб, |
(2.1) |
|
1 |
2 |
1 |
2 |
|
где α – угол между силами.
Следует подчеркнуть, что аксиома 3 справедлива для сил, линии действия которых пересекаются. Если это не так, то силы могут не иметь равнодействующей.
F1 |
α |
R |
A |
|
|
|
F2 |
|
Рисунок 2
Аксиома 4. При взаимодействии двух тел они действуют друг на друга с силами, равными по модулю, имеющими общую линию действия и направленными по ней в противоположные стороны.
В отличие от аксиомы 1, в этой аксиоме речь идет о двух силах, приложенных к разным телам. Поэтому силы взаимодействия двух тел не составляют уравновешенную систему. С другой стороны, внутренние силы, действующие между отдельными точками одной и той же механической системы, всегда уравновешивают друг друга.
Аксиома 5. Равновесие деформируемого тела не изменится, если оно станет абсолютно твердым.
Последнюю аксиому часто называют принципом отвердевания. Она позволяет рассматривать деформируемые тела, находящиеся в равновесии, как абсолютно твердые. Следовательно, все результаты, полученные в статике, могут быть использованы при анализе равновесия элементов оборудования и конструкций, деформации которых нельзя не учитывать.
Шестая аксиома статики будет сформулирована после введения ряда необходимых понятий.
18
2.2. Виды связей и вызываемые ими реакции
Движение элементов химического оборудования, как правило, не может быть произвольным. Соседние с ними элементы ограничивают их перемещение в некоторых направлениях, что сказывается на характере их возможного движения. Тела, ограничивающие перемещение рассматриваемого элемента, называются связями, а силы, за счет которых связи препятствуют его перемещению в определенном направлении, называются реакциями связей.
Таким образом, на любое материальное тело со стороны других тел могут действовать два рода сил. К первому относятся силы, способные привести в движение первоначально покоящееся тело. Они называются активными. Активные силы не зависят от величины и направления действия других сил.
Ко второму роду сил относятся реакции связей. Они называются пассивными. Пассивные силы возникают лишь тогда, когда под действием активных сил тело оказывает давление на связь. Согласно аксиоме 4 реакция связи будет равна по величине такому давлению и направлена в противоположную сторону. Следовательно, пассивные силы зависят не только от характера связи, но и от величины и направления активных сил.
Одна из важнейших задач статики – определение реакций связей, наложенных на механическую систему при равновесии. Их величина необходима для расчета внутренних усилий в конструкционном материале элементов технологического оборудования, а также непосредственно участвует при расчете опор, фундаментов, подвесок, кронштейнов и т. д.
Определение реакций связей основано на принципе освобождаемости, который составляет содержание еще одной аксиомы механики.
Аксиома 6. Всякое тело, на перемещения которого наложены ограничения, можно рассматривать как свободное, если мысленно отбросить связи, а их действие заменить соответствующими реакциями связей.
Для правильного применения принципа освобождаемости необходимо четко различать характер различных связей. Рассмотрим наиболее часто встречающиеся типы связей и их реакции, учитывая, что последние всегда направлены в сторону, противоположную направлению недопустимого перемещения.
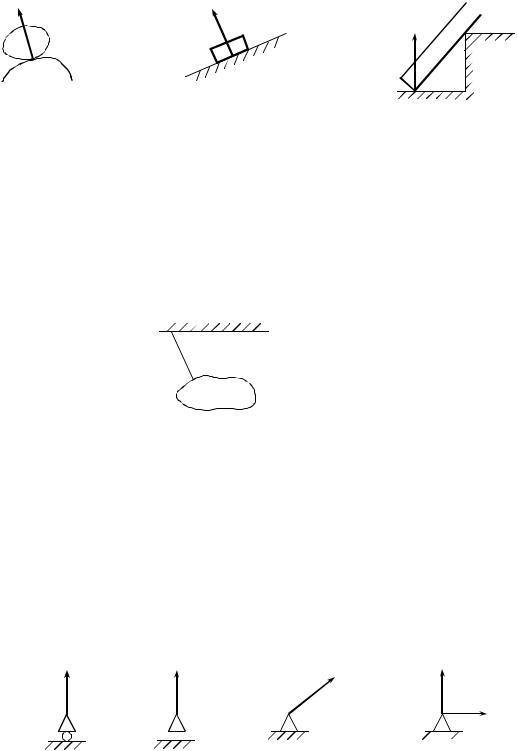
1. Гладкая поверхность. Поверхность называется гладкой, если движение по ней происходит без трения. Связь этого типа исключает перемещение тела вдоль внутренней нормали к поверхности в данной точке. Поэтому реакция связи будет направлена вдоль внешней нормали и приложена в точке касания тела и поверхности (рис. 3).
19
а R б R в R2 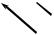
R1
 Нормаль
Нормаль
Рисунок 3
В случае угловой опоры (угловая точка нормали не имеет) реакция направлена по нормали к поверхности тела в точке соприкосновения с углом (рис. 3, в).
2. Гибкая нерастяжимая невесомая нить. Этот вид связи моделирует ограничения на перемещения тел, которые закреплены канатами, тросами и т. п. Реакция всегда направлена вдоль нити к точке ее закрепления (рис. 4).
R1 
 R2
R2
Рисунок 4
3. Шарнирно-подвижная опора. Так же как и гладкая поверхность, эта связь допускает движение тела по касательной, но препятствует перемещению как по внутренней, так и по внешней нормали к опорной поверхности. Поэтому реакция направлена перпендикулярно к ней. На практике такой тип связи реализуется при использовании опор с катками. Возможность свободного перемещения вдоль поверхности отражена в принятых для шарнирно-подвижных опор обозначениях
(рис. 5, а, б).
а R |
б R |
в |
R |
г Ry |
Rx |
|
|
|
|
|
Рисунок 5
4. Шарнирно-неподвижная опора. Этот тип связи, в отличие от предыдущей, исключает и перемещение по касательной к опорной поверхности. Реакция связи имеет неизвестное направление. Ее удобно разложить на две составляющие: по касательной и по нормали к опорной поверхности (рис. 5, в, г). При этом направление и величина
20
