MEHANIKA

Для оценки этих сил и вызванных ими напряжений рассмотрим кольцо радиуса R, вращающееся с постоянной угловой скоростью ω (рис. 43,а). Пусть А площадь поперечного сечения кольца. Величина центростремительного ускорения согласно (3.26) равна: Wn = Rω2. Определим центробежную силу, которая в данном случае играет роль силы инерции, действующую на единицу длины кольца. Масса единицы длины кольца m равна произведению объема 1∙ А на плотность ρ материала кольца: m = ρА. Тогда сила инерции Fц, действующая на единицу длины кольца, будет равна:

Fц АR 2 .

Воспользуемся методом мысленных поперечных сечений и рассмотрим силы, которые приложены к половине кольца (рис. 43,б). На обоих торцах полукольца действуют продольные силы N, которые уравновешивают всю совокупность центробежных сил, равномерно распределенных по материалу кольца. Длина элемента кольца, выделенного двумя радиусами с углом между ними dφ, равна Rdφ. Следовательно, на этот элемент будет действовать центробежная сила Fц Rdφ, проекция которой на вертикальную ось составит величину Fц Rdφ sin φ = ρAR2 ω2 sin φ dφ. Интегрируя по всему полукольцу, получаем:

2 N AR 2 2 sin d 2 AR 2 2 ,

0

откуда следует, что напряжения в материале кольца, вызванные центробежными силами равны:

Полученное выражение позволяет оценить предельные значения угловых скоростей вращающихся узлов машин, превышение которых может привести к появлению в материале опасных напряжений.

Особую роль среди динамических нагрузок играют ударные нагрузки. За счет больших ускорений при ударе возникают значительные силы инерции, которые, в конечном счете, и определяют воздействие удара. Однако точно определить величину ускорения при ударе невозможно. Поэтому воспользоваться формулой (6.14) для оценки динамических напряжений нельзя. Анализ напряжений и деформаций при ударе основан на энергетическом подходе, который приводит к результату аналогичному формуле

141

(6.14). Именно, напряжения и деформации при ударных нагрузках превышают соответствующие величины при статическом нагружении в число раз, равное динамическому коэффициенту kд. Так, при падении груза на горизонтальную балку с высоты h (рис. 44) величина динамического прогиба lд в произвольном сечении равна:

Здесь lст – величина прогиба в том же сечении при статическом нагружении.

x

yд

ℓ

Рисунок 44

Напряжения при ударе также выражаются через напряжения при статическом нагружении и динамический коэффициент kд.

Следовательно, для того чтобы рассчитать деталь на прочность и жесткость при ударных нагрузках, достаточно научиться рассчитывать

еепри внешних усилиях, не зависящих от времени.

Из формулы (6.17) можно сделать интересный вывод. Если груз не

падает с высоты, а прикладывается внезапно (h = 0), то Δσд = 2 Δσст,

т. е. при внезапном приложении нагрузки напряжения в два раза превышают напряжения, возникающие при статическом нагружении.

Поскольку, как уже отмечалось, поведение конструкционных материалов при ударно действующих нагрузках сильно отличается от поведения при статическом характере нагружения, их способность переносить мгновенное приложение внешних сил определяется с помощью специальных испытаний на удар. При этих испытаниях непосредственно измеряется количество работы, необходимой для

142

ударного излома образца. Отношение затраченной работы к площади сечения образца называется относительной вязкостью материала при ударной нагрузке. Эта величина необходима при проектировании частей машин и аппаратов, которые при эксплуатации могут подвергаться воздействию сил ударного характера.

6.4. Усталостная прочность материалов

Многие элементы химического оборудования испытывают нагрузки, периодически меняющиеся во времени. При этом в материале этих элементов возникают переменные напряжения. Характерным примером таких элементов являются вращающиеся валы, нагруженные поперечными силами. За время одного оборота каждая точка попеременно оказывается то на выпуклой, то на вогнутой стороне вала. Следовательно, в данной точке возникают то напряжения растяжения, то напряжения сжатия. Такие напряжения называют знакопеременными или циклическими. Практика показывает, что при циклических напряжениях, действующих в детали длительное время, она может разрушиться внезапно без заметных остаточных деформаций при напряжениях значительно меньше предела прочности. Это явление называют усталостью материалов. С другой стороны, способность материала сопротивляться действию циклических напряжений называют выносливостью материала. Выносливость материала характеризуется пределом выносливости.

Прежде чем дать понятие о расчетах на прочность при переменных напряжениях, рассмотрим параметры меняющихся во времени напряжений. Число периодических изменений (циклов) напряжений в единицу времени называют частотой. Максимальное σmax и минимальное σmin значения напряжений характеризуют крайние величины напряжений в данной точке материала. Их отношение

напряжения σmax и σmin равны по абсолютной величине, но противоположны по знаку. Такой цикл изменения напряжений является симметричным. При симметричном цикле среднее

напряжение σср = (σmax + σmin) / 2 равно нулю. Если σmax и σmin не одинаковы по абсолютной величине, то цикл называют

несимметричным. Наконец, при r = 0 или r = ∞ циклическое изменение напряжений называется пульсирующим.

При расчете деталей, в которых действуют циклические напряжения, основной характеристикой прочности является предел усталости (или выносливости). Под этой величиной понимают

наибольшее напряжение, которое материал в состоянии выдержать при данном значении коэффициента асимметрии

143

неограниченно большое число циклов. Значение коэффициента асимметрии указывается потому, что значения предела усталости, соответствующие различным значениям σср, различны. Если значение коэффициента r не указывается, то подразумевается предел усталости при симметричном цикле.

Для определения предела усталости проводятся специальные испытания материалов на усталость. Испытательные машины, на которых проводятся такие испытания, позволяют нагружать образец переменными нагрузками с частотой 3000 циклов в минуту и более. Поскольку предел усталости при симметричном цикле имеет наименьшее значение, то испытания обычно проводят при одинаковых по абсолютной величине σmax и σmin. Разумеется, при испытаниях образец не нагружают неограниченным числом циклов, как того требует определение предела усталости. Практика свидетельствует, что если стальной образец выдержал, не разрушаясь, 107 циклов, то он может выдержать сколь угодно большое количество циклов.

Пределы усталости определяют для различных видов деформации в зависимости от того, какие нагрузки будет испытывать та или иная деталь или элемент конструкции. Интересно сопоставить пределы усталости сталей при симметричных циклах в условиях растяжениясжатия σ-1р, изгиба σ-1 и кручения τ-1 и пределом их прочности σпр. Опытами установлено, что между перечисленными величинами существует следующая приближенная связь:

В справочной литературе обычно приводятся значения предела выносливости для конструкционных материалов, полученные при испытаниях образцов небольших диаметров (5 – 12 мм). Однако, как показывает опыт, предел выносливости зависит от размера деталей, уменьшаясь с их увеличением. Кроме того, он заметно уменьшается, если деталь имеет так называемые концентраторы напряжений. К ним относятся резкие локальные изменения формы или сечения (выточки, сверления, пазы и т. п.). На величину предела выносливости влияет также ткачество обработки поверхности. Поверхностные дефекты (царапины, риски, следы обработки) играют роль своего рода концентраторов напряжений.

Все перечисленные факторы необходимо учитывать при расчетах элементов конструкций на усталость. Они учитываются при выборе величины допускаемого напряжения, которое определяется пределом усталости, коэффициентом запаса прочности, а также коэффициентами снижения выносливости, учитывающими влияние перечисленных факторов.

144

6.5.Контрольные вопросы

1.Что называют напряженным состоянием материала в точке ?

2.Чем определяется напряженное состояние ?

3.Каков физический смысл компонент тензора напряжений?

4. В чем состоит закон парности касательных напряжений ?

5.Что такое главные площадки, главные оси и главные напряжения ?

6.Когда возникают объемное, плоское и линейное напряженные состояния материала ?

7.Сформулируйте обобщенный закон Гука.

8.Что называется предельным (или опасным) состоянием материала ?

9.Что такое эквивалентное напряжение? Какую роль оно играет при расчетах на прочность элементов конструкций, находящихся в условиях объемного напряженного состояния ?

10.Что постулирует первая гипотеза прочности? Для каких материалов она используется?

11.Сформулируйте вторую гипотезу прочности. Какое выражение для эквивалентного напряжения вытекает из этой гипотезы?

12.Какой физический механизм возникновения опасного состояния материала лежит в основе третьей гипотезы прочности?

13.Какое выражение для эквивалентного напряжения вытекает из третьей гипотезы прочности?

14.С чем связывает возникновение опасного состояния материала четвертая гипотеза прочности?

15.В каких случаях нагрузки следует считать динамическими?

16.В чем отличие динамических нагрузок от статических по характеру воздействия на детали и узлы машин и аппаратов?

17.Как используется принцип Даламбера при учете динамического характера нагрузок?

18.Что связывает динамический коэффициент? От чего зависит его величина?

19.Чем объясняется эффект нагрузок ударного действия?

20.Какие напряжения называются циклическими?

21.Что такое усталостное разрушение конструкционных материалов?

22.Что является количественной мерой способности материалов сопротивляться воздействию циклических напряжений?

23.Как проводятся испытания материалов на усталость?

24.От каких факторов зависит предел усталости (выносливости) материалов?

145

7. НАПРЯЖЕННОЕ СОСТОЯНИЕ ЭЛЕМЕНТОВ ОБОРУДОВАНИЯ, МОДЕЛИРУЕМЫХ В ФОРМЕ ОБОЛОЧКИ

Вразделе 5 были рассмотрены основы расчета на прочность, жесткость и устойчивость элементов оборудования, имеющих расчетную схему стержня. Однако для многих элементов оборудования эта расчетная схема неприменима. В первую очередь это корпуса технологических аппаратов, днища и крышки емкостей и резервуаров, перегородки и трубные решетки теплообменников, распределительные устройства скрубберов и многое другое. Перечисленные элементы оборудования приходится моделировать более сложной расчетной схемой – оболочкой. Напомним, что

оболочкой называется геометрическое тело, одно из измерений которого (толщина) существенно меньше двух других его измерений.

Внастоящем разделе расчетная схема оболочки применена в первую очередь к элементам корпусов химико-технологических аппаратов, работающих при повышенном давлении или при разрежении. Правомерность такого применения оправдана только для так называемых тонкостенных аппаратов. Тонкостенными принято считать такие сосуды и аппараты, у которых толщина стенок, по крайней мере, на порядок меньше внутреннего диаметра. Обычно тонкостенные аппараты используются для проведения технологических процессов при рабочем давлении не более 10 МПа

(100 атм).

7.1. Типовые оболочки химико-технологических аппаратов

Корпуса технологических аппаратов состоят из набора пластин и оболочек различной конфигурации, соединенных между собой как неразъемными (например, сварными), так и разъемными (например, фланцевыми) соединениями. Любая оболочка имеет две основных поверхности: внутреннюю и наружную. Условная поверхность, точки которой находятся на одинаковом расстоянии от двух основных поверхностей, называется срединной. Анализ и классификация оболочек определяются видом именно срединной поверхности.

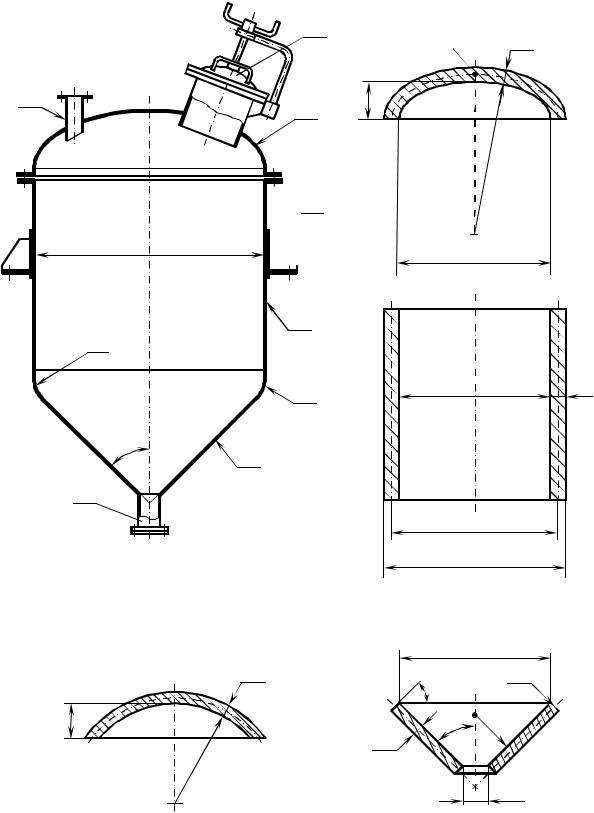
Оболочкой вращения называется такая оболочка, срединная поверхность которой образована в результате вращения плоской кривой вокруг оси, лежащей в плоскости этой кривой. Частным случаем оболочки является пластина, срединной поверхностью которой служит часть плоскости. На рис. 45, а приведена схема корпуса типичного технологического аппарата. Он содержит полный перечень оболочек, которые используются при изготовлении химического оборудования. Этот перечень включает: сферическую

146

Рисунок 45

оболочку (крышка люка 1), эллиптическую оболочку (крышка корпуса 2), пластину (фланцы отъемной крышки корпуса 3), цилиндрическую оболочку (обечайка корпуса 4, штуцера 7 и 8), торовую оболочку

147

(переходный участок корпуса 5, плавно соединяющий коническую и цилиндрическую оболочки), коническую оболочку (днище корпуса 6).

Все перечисленные оболочки являются оболочками вращения. Если такая оболочка нагружена осесимметричной внешней нагрузкой (например, давлением рабочей среды), то она называется осесимметричной. В осесимметричных оболочках картина напряжений не зависит от полярного угла. Ниже рассматриваются только осесимметричные оболочки.

Проведем плоскость через ось вращения оболочки. Эта плоскость пересечет срединную поверхность по некоторой плоской кривой, которую называют образующей или меридианом. Линия пересечения срединной поверхности плоскостью, перпендикулярной оси вращения, называется параллелью или кольцом. Степень кривизны оболочки в некоторой ее точке характеризуется кривизной меридиана и кольца в этой точке. Радиус кривизны меридиана называют первым главным радиусом кривизны оболочки в данной точке и обозначают через rm. Второй главный радиус кривизны rt численно равен длине образующей конуса с вершиной на оси вращения и боковой поверхностью, перпендикулярной срединной поверхности оболочки.

Приведем значения главных радиусов кривизны для типовых оболочек. Для конической оболочки (рис. 45, д), у которой меридианами являются прямые линии, rm = ∞, а rt = Dk / 2 cos α. Цилиндрическая оболочка (рис. 45, в) представляет собой частный случай конической (для нее угол конусности α = 0). Поэтому для нее rm = ∞, а rt = Dср/2. У сферической оболочки (рис. 45, г) оба главных радиуса кривизны одинаковы и равны радиусу срединной поверхности rm = rt = Dср/2. У пластины кривизна отсутствует. Следовательно, rm = ∞ и rt = ∞. Наконец, у эллиптической (рис. 45, б) и торовой оболочек величина главных радиусов кривизны меняется от точки к точке.

Оболочки с одним конечным главным радиусом кривизны (цилиндр, конус) называются оболочками одинарной кривизны или изогнутыми пластинами. Они могут быть изготовлены с применением недорогих технологических операций из листового материала с помощью гибки и сварки. Оболочки с двумя конечными главными радиусами кривизны (сфера, эллипсоид, тор) называются оболочками двоякой кривизны. Для их изготовления применяются более дорогие технологические операции – штамповка, литье и др.

С использованием понятия главных радиусов кривизны можно точно сформулировать условие тонкостенности элементов корпусов технологических аппаратов. Именно, если выполняется условие:

148

(где s – толщина стенки), то оболочка является тонкостенной.

7.2. Напряжения в элементах корпусов аппаратов, нагруженных внутренним давлением

Основным узлом технологического аппарата или машины является корпус, который определяет их габариты, производительность и стоимость. Корпус изолирует обрабатываемую среду, подвергаясь ее химическому воздействию и воспринимая механические и тепловые нагрузки. Следовательно, надежность работы основного химического оборудования во многом зависит от надежности его корпуса.

Под действием внешних нагрузок в материале элементов корпуса возникают напряжения, определение которых необходимо для правильного выбора толщины стенок. Чаще всего в качестве механической нагрузки выступает внутреннее давление, при котором проводится технологический процесс. Поэтому в первую очередь рассмотрим напряженное состояние корпуса, нагруженного внутренним давлением. При этом будем использовать расчетную схему оболочки, считая ее тонкостенной и осесимметричной.

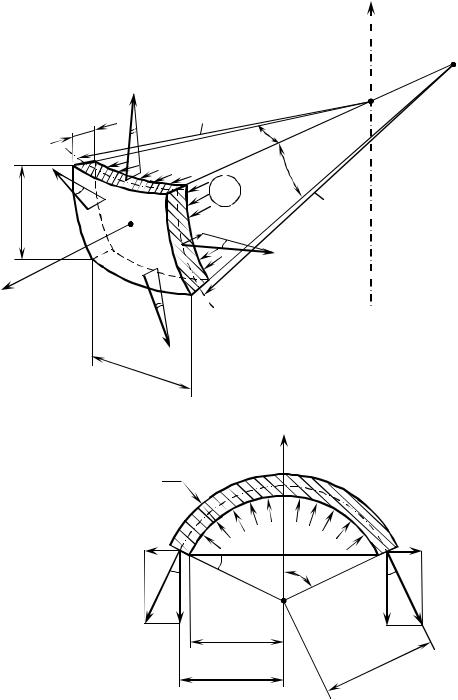
Пусть заданы величина внутреннего давления р и геометрические параметры оболочки. Под последними будем понимать толщину оболочки s и значения главных радиусов кривизны rm и rt в каждой точке срединной поверхности. Для анализа напряженного состояния материала выделим бесконечно малый элемент оболочки со сторонами dlm и dlt (рис. 46, а). Элемент выделен двумя меридиональными сечениями с углом между ними dφ и двумя нормальными коническими сечениями с углом между ними dθ. Выделенный элемент имеет четыре сечения, в каждом из которых в общем случае действуют нормальные и поперечные внутренние усилия, а также изгибающие моменты. Опыты показывают, что поперечные силы и изгибающие моменты имеют существенную величину лишь в ограниченной области вблизи так называемых линий искажения, т. е. участков, где резко меняются параметры оболочки (толщина, свойства материала, форма и направление меридиана). Поэтому, следуя безмоментной теории оболочек,

будем пренебрегать поперечными силами и изгибающими моментами

всилу их малости.

Врамках этого допущения на верхнюю и нижнюю грань выделенного бесконечно малого элемента оболочки действуют

нормальные напряжения σm и σm + dσm соответственно. Их называют меридиональными, т. к. они направлены по касательной к меридиану. На боковых гранях выделенного элемента действуют

напряжения σt (одинаковые в силу осевой симметрии), которые называют кольцевыми или тангенциальными, т. к. они направлены по

149

касательной к кольцу (параллели). Кроме того, на выделенный элемент действует давление р.

Под действием перечисленных нагрузок элемент, как и вся оболочка в целом, находится в состоянии равновесия. Следовательно, система сил, приложенных к нему, удовлетворяет уравнениям равновесия. Спроектируем все силы на нормаль n к срединной поверхности, учитывая, что сила, обусловленная

150