15. Теорема Лагранжа

Теорема. Пусть функция  дифференцируема в открытом промежуткеи сохраняет непрерывность на концах этого промежутка. Тогда существует такая точка, что

(13)

      Доказательство. Рассмотрим вспомогательную функцию

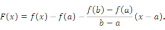
Эта функция непрерывна и дифференцируема в промежутке  , а на его концах принимает одинаковые значения:

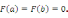
Тогда  удовлетворяет всем условиям теоремы Ролля и, следовательно, существует точка, в которой производная функцииравна нулю:

      Следствие 1. В частном случае, когда  , из теоремы Лагранжа вытекает, что существует точка, в которой производная функцииравна нулю:. Это означает, что теорема Лагранжа является обобщением теоремы Ролля.Следствие 2. Если  во всех точках некоторого промежутка, тов этом промежутке.        Действительно, пустьи– произвольные точки промежуткаи. Применяя теорему Лагранжа к промежутку, получим

Однако 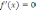 во всех точках промежутка. Тогда

Учитывая произвольность точек  и, получаем требуемое утверждение.

16. Теорема Коши

Формулировка

Геометрически это можно переформулировать так: если и задают закон движения на плоскости (то есть определяют абсциссу и ординату через параметр ), то на любом отрезке такой кривой, заданном параметрами и , найдётся касательный вектор, коллинеарныйвектору перемещения от до .

Доказательство

Для доказательства введём функцию

Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны . Воспользовавшись упомянутой теоремой, получим, что существует точка, в которой производная функцииравна нулю, аравна как раз необходимому числу.

17. Правило Лопиталя

Правило Лопиталя — метод нахождения пределов функций, раскрывающий неопределённости вида 0/0 и ∞/∞.  Суть правила: предел отношения функций равен пределу отношения их производных.

18. Экстремумы функции одной переменной. Необходимое условие экстремума.

Пусть функция f(x), определенная и непрерывная в промежутке [a,b], не является в нем монотонной. Найдутся такие части [ , ] промежутка [a,b], в которых наибольшее и наименьшее значение достигается функцией во внутренней точке, т.е. между и .

Говорят, что функция f(x) имеет в точке максимум (или минимум), если эту точку можно окружить такой окрестностью (x ₀ - ,x ₀ + ), содержащейся в промежутке, где задана функция, что для всех её точек выполняется неравенство.

f(x) < f(x ₀ )(или f(x)>f(x ₀ ))

Иными словами, точка x ₀ доставляет функции f(x) максимум (минимум), если значение f(x ₀ ) оказывается наибольшим (наименьшим) из значений, принимаемых функцией в некоторой (хотя бы малой) окрестности этой точки. Отметим, что самое определение максимума (минимума) предполагает, что функция задана по обе стороны от точки x ₀ .

Если существует такая окрестность, в пределах которой (при x=x ₀ ) выполняется строгое неравенство

f(x)<f(x ₀ )(или f(x)>f(x ₀ )

то говорят, что функция имеет в точке x ₀ собственный максимум (минимум), в противном случае – несобственный.

Если функция имеет максимумы в точках x ₀ и x ₁ , то, применяя к промежутку [x ₀ ,x ₁ ] вторую теорему Вейерштрасса, видим, что наименьшего своего значения в этом промежутке функция достигает в некоторой точке x ₂ между x ₀ и x ₁ и имеет там минимум. Аналогично, между двумя минимумами непременно найдется максимум. В том простейшем (и на практике – важнейшим) случае, когда функция имеет вообще лишь конечное число максимумов и минимумов, они просто чередуются.

Заметим, что для обозначения максимума или минимума существует и объединяющий их термин – экстремум.

Понятия максимум (max f(x)) и минимум (min f(x)) являются локальными свойствами функции и имеют место в определенной точке х ₀ . Понятия наибольшего (sup f(x)) и наименьшего (inf f(x)) значений относятся к конечному отрезку [a,b] и являются глобальными свойствами функции на отрезке.

Из рисунка 1 видно, что в точках х ₁ и х ₃ локальные максимумы, а в точках х ₂ и х ₄ – локальные минимумы. Однако, наименьшего значения функция достигает в точке х=а, а наибольшего – в точке х=b.

Поставим задачу о разыскании всех значений аргумента, доставляющих функции экстремум. При решении ее основную роль будет играть производная.

Предположим сначала, что для фунции f(x) в промежутке(a,b) существует конечная производная. Если в точке х ₀функция имеет экстремум, то, применяя к промежутку (х ₀ - ,х ₀ + ), о которой была речь выше, теорему Ферма, заключаем, что f (x)=0 этом состоит необходимое условие экстремума. Экстремум следует искать только в тех точках, где производная равна нулю.

Не следует, думать, однако, что каждая точка, в которой производная равна нулю, доставляет функции экстремум : указанное только что необходимое условие неявляется достаточным.