Переход к новому базису

Пурть в пространстве R имеются два базиса: старый e_l, e₂,...e_nи новый e _l^*, e₂^*,...e_n^*. Любой вектор нового базиса можно представить в виде линейной комбинации векторов старого базиса:

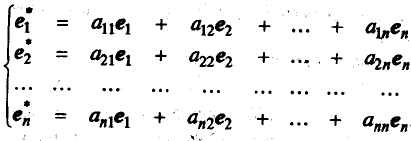
Переход от старого базиса к новому можно задать матрицей перехода

Отметим, что коэффициенты размножения новых базисных векторов по старому базису образуют столбцы, а не строки этой матрицы.

Матрица А - неособенная, так как в противном случае ее столбцы (а следовательно, и базисные векторы) оказались бы линейно зависимыми. Следовательно, она имеет обратную матрицу А^-1.

Пусть вектор Х имеет координаты (х_l, х₂,... х_n) относительно старого базиса и координаты (х_l^*, х₂^*,... х_n^*) относительно нового базиса, т.е. Х = x_le_l + x₂e₂ +...+ x_ne_n = x_l^*e_l^* + x₂^*e₂^* +...+ x_n^*e_n^*.

Подставим в это уравнение значения e_l^*, e₂^*,...e_n^*из предыдущей системы:

x_le_l + x₂e₂ +...+ x_ne_n = x_l^*(a₁₁e_l + a₁₂e₂ + … + a_1ne_n) + x₂^*(a₂₁e_l + a₂₂e₂ + … + + a_2ne_n) +...+ x_n^*(a_n1e_l + a_n2e₂ + … + a_nne_n)

0 = e_l( x_l^*a₁₁ + x₂^*a₂₁ + … + x_n^*a_n1 - x_l) + e₂( x_l^*a₁₂ + x₂^*a₂₂ + … + x_n^*a_n2 – x₂) + + … + e_n( x_l^*a_1n + x₂^*a_2n + … + x_n^*a_nn – x_n)

В силу линейной независимости векторов e_l, e₂,...e_nвсе коэффициенты при них в последнем уравнении должны равняться нулю. Отсюда:

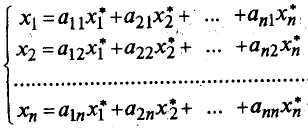
или в матричной форме

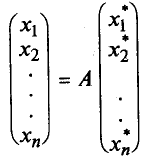
Умножим обе части на А^-1, получим:

Например, пусть в базисе e_l, e₂, e₃заданы вектора а₁= (1, 1, 0), а₂= (1, -1, 1), а₃= (-3, 5, -6) иb= (4; -4; 5). Показать, что вектора а_l, а₂, а₃тоже образуют базис и выразить в этом базисе векторb.

Покажем, что вектора а_l, а₂, а₃линейно независимы. Для этого убедимся в том, что ранг составленной из них матрицы равен трем:

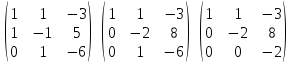
Отметим, что исходная матрица представляет собой не что иное, как матрицу перехода А. В самом деле, связь между базисами e_l, e₂, e₃и а_l, а₂, а₃ можно выразить системой:

Вычислим А^-1.

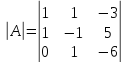= 6 + 0 - 3 – 0 – 5 + 6 = 4

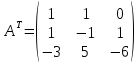
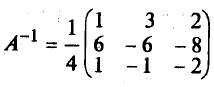
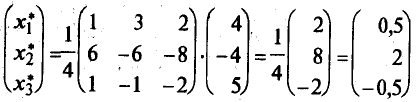
Т. е. в базисе а_l, а₂, а₃векторb= (0,5; 2; -0,5).

Линейные операторы

Линейным оператором (преобразованием, отображением)n-мерного векторного пространства называется правилоY=f(X), по которому каждому вектору Х ставится в соответствие единственный векторY, причем сохраняются линейные операции над векторами, т.е. имеют место свойства:

1) f(X+Z) =f(X) +f(Z) - свойство аддитивности оператора;

2) f(X) =f(X) - свойство однородности оператора.

Можно доказать, что каждому линейному оператору соответствует квадратная матрица в данном базисе. Справедливо и обратное: всякой матрице n-го порядка соответствует линейный оператор n-мерного пространства.

Поэтому линейное преобразование можно определить по-другому: линейным оператором n-мерного векторного пространства, заданным квадратной матрицей А, называется преобразование, которое любому векторуX, записанному в виде матрицы-столбца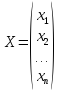, ставит в соответствие вектор А(Х) = А*Х =.

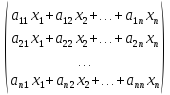Матрицу А называют матрицей операторав данном базисе, а ранг этой матрицы -рангом оператора.

Например, если линейный оператор задан матрицей 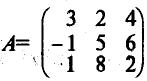, то отображениеYвектораX= (4, -3, 1) будет равно

.

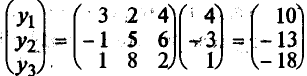Отметим, что единичная матрица задает тождественное преобразование (тождественный оператор), поскольку, умножая ее на вектор, мы получаем тот же самый вектор.

Нулевая матрица определяется, как нулевой оператор, переводящий все векторы пространства в нулевые векторы.

Легко убедиться, что диагональная матрица, на диагонали которой стоит одно и то же число, задает оператор умножения вектора на это число.

Теорема. Матрицы А и А^*одного и того же линейного оператора в базисах e_l, e₂,...e_nи e_l^*, e₂^*,...e_n^*связаны соотношением А^*= С^-1АС, где С - матрица перехода от старого базиса к новому.

Доказательство. Обозначим Yотображение вектораXв базисee_l, e₂,...e_n, а те же вектора в базисе e_l^*, e₂^*,...e_n^*обозначим Х^*и Y^*. Так как С - матрица перехода, можно записать:

X = СХ^*

Y = CY^*

Умножим слева обе части первого равенства на матрицу А:

АX = АСХ^*

Так как АX = Y, получимY= АСХ^*, т.е. CY^*= АСХ^*. Домножив обе части последнего равенства на С^-1, получим:

С^-1CY^*= С^-1АСХ^*

Y^*= С^-1АСХ^*.

Так как Y^*= А^*X^*, А^*= С^-1АС, что и требовалось доказать.

Например, пусть в базисе e_l, e₂матрица оператора А =. Найти матрицу этого оператора в базисе e_l^*= e_l-2e₂, e₂^*= 2e_l+ e₂.

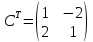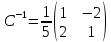Для этого построим матрицу перехода С = и обратную ей матрицу С^-1.|C|= 5,,. Тогда