2009 Методы контроля и анализа

При измерении линейкой точность измерения составляет приблизительно 0,2 мм (при измерении компаратором ― 0,001 мм). Линейку с пленкой скрепляют таким образом, чтобы край линейки с делениями проходил через «экваториальную» линию. Поскольку дифракционная линия имеет некоторую ширину, то измерения лучше производить до середины ее ширины. Результаты измерений заносят в табл. 3.1;

Таблица 3.1

Расчет параметра решетки при асимметричной закладке пленки

Примечание:

LA ― измерение положения относительно выбранного начала координат линий, расположенных слева от выхода;

LB ― измерения до симметричных линий с той же нумерацией, расположенных справа от выхода (сюда же относятся измерения до линий, не имеющих слева симметричной пары);

LD ― измерения до всех линий, расположенных справа от входа;

LC ― измерения до симметричных им линий, расположенных слева от входа и имеющих ту же нумерацию.

5 ― рассчитать эффективную длину окружности пленки, т. е. фактическую длину в момент измерений.

Для каждого кольца находят сумму указанных измерений

21

ΣЛ = LA + LB или ΣК = LC + LD .

Определяют среднее арифметическое результатов вычислений для всех колец, расположенных вокруг выхода ΣЛ и вокруг вхо-

да ΣК . (В расчет сумм измерений не входят линии, не имеющие симметричной пары).

Расстояние между точками К и Л должно соответствовать дуге 180°, так как они лежат на концах одного и того же диаметра. Поэтому эффективную длину окружности пленки можно найти из соотношения:

2πRэф = ΣК − ΣЛ;

6 ― определить радиусы и диаметры дебаевских колец. Вначале вычисляют координату центра выхода рентгеновских лучей,

Радиусы дебаевских колец lизм определяются вычитанием из

LВ и LС координаты центра выхода Цл (в мм): lизм = LВ(LС) − Цл

Затем подсчитываются диаметры колец 2lизм;

7 ― ввести поправку на поглощение лучей образцом, т. е. найти исправленный диаметр дебаевских колец 2lиспр.

Поскольку образец имеет некоторую толщину и проходящие лучи частично поглощаются, то измеренные расстояния между линиями всегда будут больше, чем истинные. Поэтому из найденных значений 2lизм необходимо вычесть поправку на толщину образца.

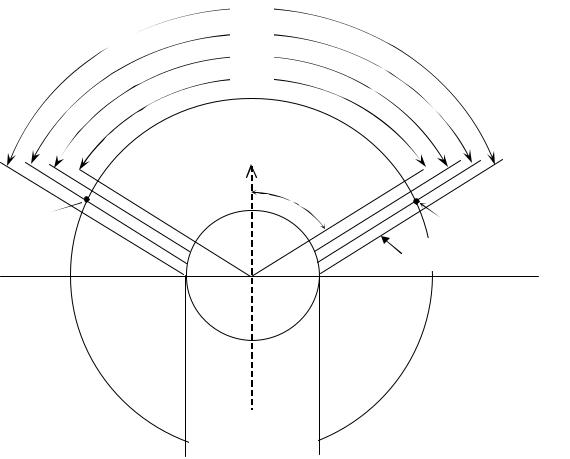
На рис. 3.2 показана схема расчета поправки на поглощение рентгеновских лучей образцом. Если бы образец не поглощал лучи, отраженные лучи исходили бы из одной точки (центра образца). Расстояние А1А между серединами линий равнялось бы 2lисп. В действительности вследствие поглощения в отражении участвует поверхностный слой образца ВС и В1С1. Середина линий определяется точками Р и Р1. Отсюда следует, что при измерении расстояния между линиями по внешним краям истинное расстояние между ними таково:

22

2lисп = 2lизм – 2r,

где 2r ― диаметр образца.

При измерении расстояния между внутренними краями линий:

2lисп = 2lизм – 2r cos2Θ.

При измерении между серединами линий:

2lисп = 2lизм – r (1+cos2Θ ).

2lнар

2lср

2lвн

2lисп

Первичный

пучок

Рис. 3.2. Схема расчета поправки на поглощение образцом рентгеновских лучей

При съемке в стандартной камере РКД (диаметр которой равен 57,3 мм) считаем, что 1 мм линейных измерений по окружности пленки приблизительно соответствует 1°. Поэтому значение угла Θ

23

для вычислений берется приближенным и численно равным lизм. В расчетах, не требующих высокой точности, поправку вычисляют с точностью ±0,05 мм. Значения сомножителя (1+cos2Θ ) в зависимости от угла Θ даны в Приложении П.1;

8 ― рассчитать углы отражения.

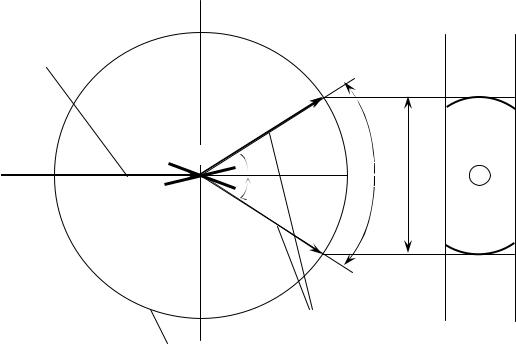
Первичный пучок рентгеновских лучей с длиной волны λ, попадая на образец (рис. 3.3), отражается от плоскостей РР и Р1Р1 под

углом, удовлетворяющим уравнению Вульфа−Брегга (nλ = 2d sinΘ), и дает дифрагированные лучи КМ и КМ1 соответственно. Дифрагированное излучение образует конус с углом раствора 4Θ. Пересечение этим конусом цилиндрической фотопленки образует на дебаеграмме дифракционное кольцо. Угол 4Θ соответствует на пленке расстоянию 2lисп, а 360o ― длине окружности 2πRэф.

Следовательно,

Рис. 3.3. Схема формирования дифракционных колец на пленке в камере РКД

24

9 ― вычислить значения sinΘ с точностью до четвертого зна-

ка;

10 ― произвести определение α- и β-линий. Рентгенограмма, полученная в не фильтрованном излучении,

представляет собой последовательность отражений как α−, так и β−характеристического излучения.

Для каждой кристаллографической плоскости HKL, согласно формуле Вульфа−Брегга, выполняются условия

nλα = 2dHKL sin Θα nλβ = 2dHKL sin Θβ

Поскольку λβ< λα, β-линии располагаются под меньшими углами Θ.

ме ― β−линия, то при умножении синуса угла дифракции этой линии на отношение длин волн используемого α− и β−характеристического излучения должна получиться величина, равная синусу угла Θ одной из последующих линий (которая и будет

соответствующей α−линией). В том случае, если такого совпадения не нашлось, предположение было неверным, и на самом деле первая линия дебаеграммы является α−линией (а соответствующее ей β−отражение на пленке отсутствует, так как является слишком слабым). При этом следует учитывать, что интенсивность β−линий должна быть меньше, чем интенсивность соответствующих α−линий. (Иногда интенсивность может увеличиваться за счет наложения линий различных фаз при съемке многофазных образцов).

25

Затем рассматривают следующую линию как линию β- излучения и т. д.

Дальнейший расчет ведут только для α−линий; 11 ― вычислить sin2Θ для α−линий;

12 ― произвести индицирование рентгенограммы.

Под индицированием линий рентгенограммы понимают операцию определения индексов дифракции HKL каждой дифракционной линии рентгенограммы.

Из квадратичной формулы для величины межплоскостного

тов синусов углов отражения для разных линий рентгенограммы должны быть равны соответствующему отношению сумм квадратов индексов дифракции и, следовательно, отношению целых чисел:

Ряд данных отношений для всех линий рентгенограммы в порядке возрастания углов должен представлять собой строго определенный ряд чисел, различный для кубических решеток разного типа (табл. 3.2). Задача индицирования сводится к нахождению от-

ношений sin2Θn+1/sin2Θ1 и сопоставлению полученного ряда с данными табл. 3.2. Далее определяют тип кубической решетки и индексы дифракции каждой линии.

Cуществует некоторая неопределенность при выборе решеток К6 (примитивной) и К8 (объемно-центрированной). Однако необходимо помнить, что для примитивной решетки большую интенсивность будет иметь вторая линия, а для объемноцентрированной ― первая. Относительная интенсивность линий рентгенограммы с близкими углами Θ определяется, прежде всего, фактором повторяемости p. Известно, что для линий 100 и 200 фактор повторяемости соответствующих отражающих плоскостей p=6, а для линий 110 ― 12.

26

27

На рентгенограмме, снятой с примитивной кубической решетки К6, присутствуют все возможные линии; на рентгенограмме ОЦК−

(К12) ― только линии одинаковой четности (нуль считается четным числом);

13 – определить параметры элементарной решетки, используя квадратичную форму для кубической решетки:

Точные значения параметра кристаллической решетки получаются на линиях, расположенных под наибольшими углами, так как с увеличением угла ошибка определения уменьшается. Поэтому вычисления можно провести по одной или двум последним линиям.

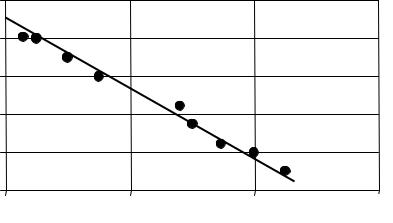
14 ― для более прецизионных измерений параметра кубической решетки и рекомендуется построить зависимость значения па-

раметра a от экстраполяционной функции Нельсона−Тейлора

(рис. 3.4):

Такая функция является линейной в большом диапазоне уг-

лов.

Значения экстраполяционной функции в зависимости от угла Θ даны в Приложении П.2;

15 ― рассчитать погрешность определения параметра решет-

ки.

Ошибки в определении Θ делятся на две группы: случайные, вызванные неточностью измерений, и систематические, связанные с геометрией съемки и особенностями взаимодействия рентгеновских лучей с веществом. Ошибки вследствие деформации пленки и неточности определения диаметра камеры были исключены асимметричным способом съемки. Ошибка из-за поглощения излучения в образце учтена с помощью введения соответствующей

28

a, Å 3,620

3,616

3,612

3,608

3,604

3,600

Рис. 3.4. Пример экстраполяционного графика для определения параметра решетки

поправки. Когда замеры производят посередине линий, то ошибкой, вносимой эксцентриситетом образца, можно пренебречь. Таким образом, основной источник ошибки ― неточность измерений угла дифракции. Тогда абсолютная погрешность определения параметра решетки

Дебая (57,3 мм); 2Rэф ― эффективный диаметр камеры, определяемый по эффективной длине окружности пленки; l ― абсолютная погрешность измерения положений линий (для измерений с помощью линейки l = 0,2 мм). Значение ΔΘ вычисляется в радианах.

Погрешность определяют по одной из двух последних линий дебаеграммы;

16 ― по вычисленному параметру элементарной ячейки и типу решетки определить исследуемое вещество;

17 ― для проверки правильности установления типа решетки рассчитать число атомов, приходящихся на элементарную ячейку:

29

n = VAmρ ,

где V ― средний объем элементарной ячейки, (м-10)3; ρ ― плотность исследуемого вещества, кг/м3; A ― средний атомный вес вещества; m ― условная масса атома водорода (1,66020.10-27 кг).

Известно, что для примитивной решетки n = 1, для ОЦК n = 2, для ГЦК n = 4.

Средний объем элементарной ячейки для кристаллов:

При исследовании твердых растворов по числу атомов в элементарной ячейке можно установить тип твердого раствора. В твердом растворе замещения число атомов в элементарной ячейке n совпадает с числом атомов в ячейке данной кристаллической структуры. В твердых растворах внедрения n всегда должно быть больше величины для данного типа ячейки. В твердых растворах вычитания n всегда меньше нормального значения.

Содержание отчета:

1 ― указать номера образца и камеры, тип излучения, длины волн излучения λα и λβ время экспозиции, напряжение и силу тока

на трубке, диаметры камеры и образца; 2 ― результаты вычислений представить в виде таблицы;

3 ― построить график экстраполяции (значение экстраполированного параметра решетки определяется по методу наименьших квадратов);

4― вычислить погрешность расчета;

5― проверить правильность определения типа кубической решетки, вычислив число атомов в элементарной ячейке.

30