§ 3. Цилиндрические функции. Уравнение Бесселя

Запишем уравнение Бесселя

(1)

Нетрудно видеть, что является особой точкой уравнения. Об этом нужно помнить, когда умножая его почленно на x², мы приходим к формуле (1). Уравнение, записанное в виде (1) или в виде (3), называют уравнением Бесселя ν-го порядка или уравнением цилиндрических функций ν-го порядка. Второе название объясняется тем, что к этому уравнению в задачах математической физики приходят в случае применения метода разделения переменных, когда (в силу специфики граничных условий) используются полярные или цилиндрические координаты. Проследим этот путь на примере решения задачи о свободных колебаниях круглой мембраны, которая формулируется следующим образом.

Требуется найти нетривиальное и ограниченное внутри круга решение уравнения колебания струны в полярных координатах

, (2)

удовлетворяющее однородному граничному условию

(3)

где l – радиус круга и начальным условиям

(4)

Представим U в виде

. (5)

Это возможно только тогда когда существует λ, такое что

. (6)

Для уравнения (6) граничные условия перепишутся следующим образом:

(7)

(8)

Начальные условия можно выписать только для произведения функций .

II шаг: Рассмотрим функцию V:

. (9)

Граничные условия имеют вид R(l)=0. (10)

Если мы введем переменные , то получим следующее уравнение

(13)

Это уравнение является частным случаем уравнения Бесселя для задачи о колебании круглой мембраны. В общем случае вместо коэффициента n, равного целому числу, должен стоять произвольный параметр ν, а именно

(13')

Решение уравнения Бесселя.

Будем искать решение уравнением Бесселя в виде обобщенного степенного ряда

или (14)

Чтобы определить коэффициенты ряда (14) нужно подставить его в уравнение (13) и собрать коэффициенты при одинаковых степенях х . После этого полученные коэффициенты при каждой степени х приравняем нулю, в результате получим

коэффициент при :

и если, то будет следовать, что . Положим сначала, а потом окончательное решение запишем и для .

Коэффициент при :

или

, но вспоминая, что, будем иметь

Поскольку, получаем, что .

Коэффициент при :

или

, т.е.

и в результате будем иметь

при этом a₀ остается не определенным (а значит, произвольным)

Имея выражение a₂ через a₀ можно предположить (и доказать), что и a_к будет выражаться через a_к-2 аналогичным образом , т. е.

()

В частности:

Тогда можно записать

()

Воспользуемся свойством гамма-функции

,

но и тогда

Если теперь выберем для произвольного a₀ выражение , то

Тогда решение уравнения Бесселя можно записать в виде

функция Бесселя (15)

для :

.

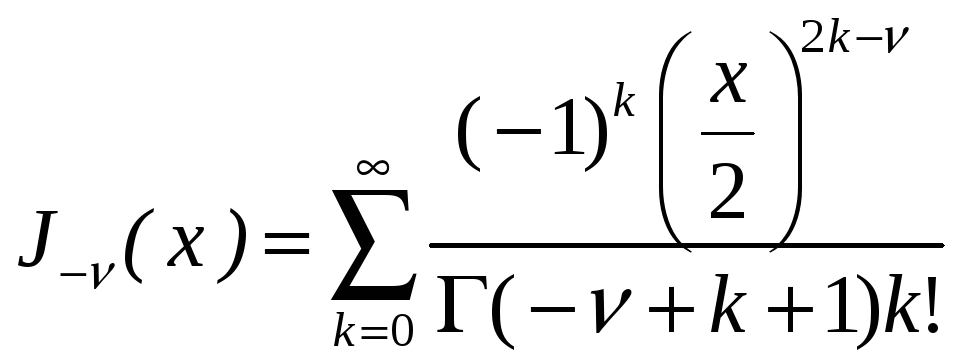Если ν – не целое число, то и являются линейными независимыми функциями, и из них можно составить общее решение уравнения. Если ν – целое, то можно показать, что .

В этом случае вводят в рассмотрение комбинацию из и следующего вида:

, (16)

которая также является решением уравнения Бесселя и, кроме того, является линейно независимой функцией от .

называется функцией Неймана, которая тоже является специальной функцией.

При решении задачи о колебании мембраны у нас как раз – целое число и общее решение надо бы писать в виде

Однако, вспоминая граничное условие и условие , мы видим, что в нуле неограниченно возрастает и, следовательно, надо положить .

Таким образом, общее решение имеет вид

(17)

Для определения значений λ воспользуемся граничным условием в виде

(для каждого n) (18)

и получаем бесконечный набор трансцендентных уравнений, каждое из которых будет иметь бесконечное число решений (для каждого m), т.е., где m и n – целые числа. Тогда и функции Бесселя должны иметь двойную нумерацию J_{n m}.