Тема 4 Системы уравнений

Достаточное условие идентификации (ранговое условие)

Чтобы уравнение, входящие в систему одновременных уравнений было идентифицировано, необходимо и достаточно, чтобы ранг матрицы коэффициентов по отсутствующим в нем переменным был на единицу меньше числа эндогенных переменных в системе и определитель этой матрицы не был равен нулю.

 Первое уравнение: Н=3 и D=2, т. е. D+1=H

Коэффициенты при отсутствующих в первом уравнении переменных

Определитель матрицы (detA) коэффициентов равен 0. Достаточное условие идентификации не выполняется.

Уравнение неидентифицируемо

 Второе уравнение: Н=2 и D=1, т.е. D+1=Н

detA≠0, ранг матрицы равен 2. Достаточное условие идентификации выполняется.

Уравнение точно идентифицировано.

 Третье уравнение: Н=3 и D=2, т.е. D+1=Н

 detA=0. Достаточное условие идентификации не выполняется.

 Уравнение не идентифицировано.

Оценивание параметров в структурной форме моделей

Косвенный метод наименьших квадратов (КМНК).

Двухшаговый метод наименьших квадратов (ДМНК)

Косвенный метод наименьших квадратов (КМНК)

Строится приведенная форма модели.

Для каждого уравнения приведенной модели традиционным МНК оцениваются параметры модели.

Коэффициенты приведенной модели трансформируются в параметры структурной модели.

ПРИМЕР

Структурная форма модели

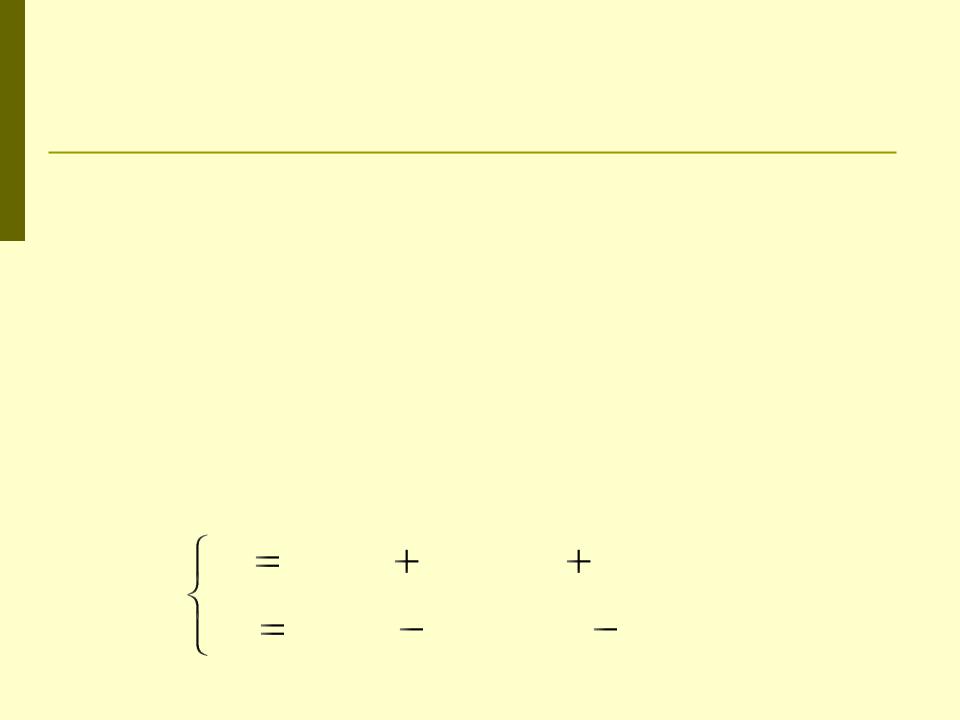
 Приведенная форма модели