
3922 / лаб2
.pdf
13
Лабораторная работа № 2
МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ МНОГОКРИТЕРИАЛЬНОЙ ЛИНЕЙНОЙ ОПТИМИЗАЦИИ
Цель работы: изучение и сравнительный анализ методов решения задачи многокритериальной линейной оптимизации; реализация этих методов средствами программы Microsoft Excel и практическое решение многокритериальных задач линейной оптимизации на ЭВМ.
1.ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Вобщем случае задача формулируется следующим образом. Найти
вектор
x (x |
, x |
2 |
,...,x |
n |
) |
1 |
|
|
|
управляемых параметров, который обеспечивает
одновременно максимальные (минимальные) ных критериев оптимальности, например:
max f1 (x); |
max f2 (x); |
….; |
x X |
x X |
|
значения нескольких част-
max f |
p |
(x), |
x X |
|
|
|
|
где область допустимых решений X задается системой ограничений вида
g |
(x) 0 |
(i 1,k); |
i |
|
|
g |
(x) 0 |
(i k 1,m). |
i |
|
|
Анализ задач многокритериальной оптимизации значительно упрощается, если ввести понятие области критериев, которая определяется с использованием значений частных критериев оптимальности и представляется как множество
Y {y ( y1, y2 ,...,y p ) : yk fk (x), k 1, p, x X}. |
||
Область критериев Y является отображением множества допустимых |
||
решений X в p-мерное пространство R |
p |
, где R – множество вещественных |
|
||
чисел, причем каждому вектору x X |
соответствует y Y . |
|
Область критериев Y можно разделить на два подмножества:
Y = Y(c) Y(к); Y(c) Y(к) = ,
называемых областью согласия Y(c) и областью компромисса Y(к).
В области согласия нет противоречий между частными критериями оптимальности. Если y Y(c), то соответствующая точка x X может быть
изменена таким образом, что все частные критерии будут одновременно увеличены. В случае, когда область критериев Y = Y(c) состоит только из области согласия, существует единственная точка x* X , в которой все частные критерии оптимальности согласованы между собой, т.е. при дви-
жении к x * значения всех функций yk fk (x), k 1, p, одновременно воз-
растают.
Такая ситуация на практике встречается очень редко. Наиболее типичным является случай, когда максимум по каждому частному критерию

14
достигается в различных точках |
xk* |
В этих точках компоненты векторного
X , k 1, p,
критерия
где
y (
fk (xk*) max fk (x) . |
|
x X |
|
y1, y2 ,...,y p ) |
являют- |
ся противоречивыми.
Такое противоречие означает, что для некоторой точки
существует ни одной другой точки x X , в которой |
fk (x) |
x |
X |
0 |
|
fk (x0 )
не
для
всех частных критериев ( неравенство строгое, т.е.
k 1, |
|
f |
(x) |
l |
|
p
) и хотя бы для одного критерия
fl (x0 ) . Очевидно, что в точке |
x0 |
f |
(x) |
l |
|
X |
|
это век-
торный критерий не может быть увеличен для всех частных критериев одновременно. Поэтому решение, соответствующее точке x0 X , называется
неулучшаемым решением или решением, оптимальным по Парето.
Оптимальность по Парето означает, что нельзя далее увеличить зна-
чение критерия |
fl (x) , не уменьшая при этом хотя бы один из других част- |
ных критериев. |
Множество всех точек x0 X 0 , оптимальных по Парето, |
соответствует значениям
y0
Y(к), составляющим область компромисса Y(к),
и называется областью (множеством) Парето.
Таким образом, проблему поиска оптимальных решений по нескольким критериям называют векторной оптимизаций. Решение задачи векторной оптимизации x0 X 0 , в котором значения всех частных критериев
были бы пусть не оптимальными, но наилучшими по выполнению всех критериев одновременно, можно найти в области Парето X0. Такие реше-
ния называют эффективными, компромиссными или оптимальными по Парето, а область X0 X, в которой невозможно одновременное улучшение всех критериев, находится в области допустимых решений X задачи.
Следует заметить, что при решении задач векторной оптимизации возникает ряд специфических проблем, к которым относятся:
-нормализация критериев, т.е. приведение их к единой шкале измерений, если частные критерии имеют различные единицы измерения;
-ранжирование критериев по приоритетам (их важности);
-выбор схемы компромисса, т.е. определение правила сравнения нескольких решений с векторными критериями оптимальности.
Число возможных схем компромисса является достаточно большим. Наиболее известные из них получают по методам обобщенного критерия, главного критерия, минимаксного критерия, последовательных уступок и др.
1.1.Решение задачи многокритериальной линейной оптимизации методом равных и наименьших относительных отклонений
Пусть необходимо найти компромиссное решение задачи линейной оптимизации, в которой имеется p > 1 линейных частных критериев вида

15
|
n |
(1) |
|
|
|
f |
c |
x |
|
||
j |
j |
||||
1 |
j 1 |
|
|||
|
|
|
|
max
;
|
|
n |
(2) |
|
|
|
f |
|
c |
x |
|
||
2 |
j |
j |
||||
|
j 1 |
|
||||
|
|
|
|
|
max
; … ;
|
|
n |
( p) |
|
|
|
f |
|
c |
x |
|
||
p |
j |
j |
||||
|
j 1 |
|
||||
|
|
|
|
|
max
,
(1)
а система ограничений задается аналогично задаче линейного программирования следующим образом:
n |
|
|
b |
a |
x |
j |
|
ij |
|
i |
|
j 1 |
|
|
|
(
i
1, m
);
x |
j |
0 |
|
|
( j 1, n ).
(2)
Обозначим через
f |
k |
* |
|
|
максимальное значение критерия
fk
, получен-
ное в результате решения задачи линейного программирования с един-
ственной целевой функцией
|
|
n |
(k ) |
|
|
|
f |
|
c |
x |
|
||
k |
j |
j |
||||
|
j 1 |
|
||||
|
|
|
|
|
при ограничениях (2). Предполо-
жим, что
f |
* 0 |
k |
|
для всех
k
1,
p
. Поскольку
f |
k |
* |
|
|
могут иметь разные зна-
ки, то для удобства представим исходную задачу таким образом, чтобы значения всех частных критериев, полученные для каждого из них в отдельности без учета других, были бы положительными.
Разобьем все множество частных критериев F = {f1, f2, …, fp} на два непересекающихся подмножества F1 { fs : fs* 0} и F2 { ft : ft* 0}. За-
тем, сохраняя эквивалентность исходной задачи, введем новые частные критерии оптимальности:
где
f |
|
t |
|
|
z |
|
|
f |
|
|
|
s |
s |
||||
|
|
|
||||
|
|
|
|
|||
|
|
|
|
|
|
|
z |
|
f |
||||
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
их экстремальные
F2 .
|
n |
|
(s) |
|
|
|
|
|
|
|
c |
x |
|
max, |
|||||||
j |
j |
|||||||||
|
j 1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
n |
|
(s) |
|
|
min, |
|||
|
c |
x |
|
|||||||
t |
j |
|
j |
|||||||
|
|
j 1 |
|
|
|
|
|
|
||
|
значения |
|
zs* fs* |
|||||||
f |
s |
F ; |
|
||
|
|
|
1 |
|
|
|
|
f |
F |
, |
|
|
|
t |
|
2 |
|
|
для |
fs F1 |
|||
и
z |
* f |
* |
t |
t |
|
(3)
для
Тогда, учитывая, что |
zk* 0 |
для всех |
k 1, p , условие равенства от- |
носительных отклонений значений частных критериев от их экстремальных значений можно записать как
z * z |
|
z * z |
2 |
... |
z p* z p |
|
|
|||
1 |
1 |
2 |
|
|
|
. |
(4) |
|||
|
z * |
z * |
|
z |
|
* |
||||
|
|
|
|
p |
|
|
||||
|
1 |
|
2 |
|
|
|
|
|
|
|
Выполним анализ условия (4) с целью исключения операции определения абсолютной величины. Для этого рассмотрим произвольную пару
критериев zs и zt . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Пусть |
zs , zt F1, т.е. эти частные критерии максимизируются. Тогда |
||||||||||||||||||||||||
|
|
|
|
|
|
zs* zs |
|
zt* zt |
|
или |
1 |
|
1 |
z |
|
1 |
1 |
z |
|
, |
(5) |
||||||
|
|
|
|
|
|
|
|
|
s |
|
t |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
zs* |
|
|
zt* |
|
|
|
|
|
|
|
zs* |
|
|
zt* |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
поскольку |
оба числителя |
z * z |
s |
и |
z |
* z |
t |
|
положительны. |
Обозначим |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|||||||||||||||||||||
|
d |
k |
для всех k 1, p и подставим в (5). Это условие будет иметь вид: |
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
zk* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

16
ds zs dt zt |
или |
ds zs dt zt 0 . |
(6) |
Если рассмотреть критерии |
zs , zt |
F2, которые одновременно ми- |
нимизируются, то получим точно такое же уравнение (6), так как направления их оптимизации также совпадают.
В том случае, когда zs F1, |
zt F2 |
или |
zs F2, |
zt F1, т.е. критерии |
|||||||
zs и zt имеют разные направления оптимизации, получаем |
|||||||||||
z * z |
|
|
z * z |
|
|
|
|||||
s |
|
|
|
s |
t |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
||||
|
z |
s |
* |
|
|
|
z |
* |
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
или с учетом введенных обозначений |
|
|
|
|
|
|
|||||
ds |
fs |
dt ft 2 . |
|
|
(7) |
||||||
Таким образом, равенство относительных отклонений для любых |
|||||||||||
двух частных критериев zs и zt |
|
имеет вид (6), если направления их опти- |
|||||||||
мизации совпадают, или (7), если они противоположны.
Чтобы получить компромиссное решение исходной многокритериальной задачи с ограничениями (2) и частными критериями оптимальности
(3) методом равных и наименьших отклонений, необходимо решить расширенную задачу линейного программирования, которая формулируется
следующим образом. |
|
|
Шаг 1. Дополнительно к переменным |
x j 0 |
( j 1, n ) исходной за- |
дачи вводятся неотрицательные переменные |
zk 0 |
( k 1, p ). |
Шаг 2. В качестве целевой функции выбирается один любой частный критерий оптимальности, например, z1 F1, где
|
n |
(1) |
|
|
|
z |
c |
x |
|
||
j |
j |
||||
1 |
j 1 |
|
|||
|
|
|
|
max
.
(8)
Шаг 3. В систему ограничений (2) вводятся p дополнительных уравнений, определяющих возможные значения переменных zk ( k 1, p ):
n |
(1) |
x |
|
z |
c |
|
|||
|
|
|
|
|
j 1 |
j |
|
j |
1 |
|
|
|
|
0
;
n |
(2) |
x |
|
z |
|
c |
|
|
|||
|
|
|
|
|
|
j 1 |
j |
|
j |
|
2 |
|
|
|
|
|
0
; …;
n |
( p) |
x |
|
z |
|
c |
|
|
|||
|
|
|
|
|
|
j 1 |
j |
|
j |
|
p |
|
|
|
|
|
0
.
(9)
Шаг 4. В систему ограничений вводятся p-1 дополнительных уравнений, устанавливающих равенство относительных отклонений частных критериев от их экстремальных значений:
d1z1 dk zk 0 , zk F1 \ {z1}; |
(10) |
d1z1 dk zk 2 , zk F2 . |
(11) |
Если частный критерий zk имеет такое же направление оптимизации, что и целевая функция (8), т.е. критерий z1, то добавляется ограничение (10), если противоположное, то ограничение (11).
Таким образом, компромиссное решение задачи многокритериальной линейной оптимизации можно получить, если решить расширенную задачу линейного программирования с целевой функцией (8) и ограничениями
17
(2), (9) - (11) при условии неотрицательности всех переменных. При этом нетрудно заметить, что с учетом условия (4) максимизация целевой функции z1 обеспечивает минимизацию относительных отклонений всех частных критериев от их экстремальных значений.
Замечание. Если необходимо улучшить значения каких-то критериев, то в условие (4) вводятся весовые коэффициенты 2, 3,…, p, где1 = 1, учитывающие важность частных критериев относительно целевой функции z1:
z * z |
|
z * z |
2 |
|
z p* z p |
|
|||||
1 |
1 |
2 |
2 |
|
... p |
|
|
|
. |
||
|
z * |
z * |
|
|
z |
|
* |
||||
|
|
|
|
|
|
p |
|
||||
|
1 |
|
2 |
|
|
|
|
|
|
|
|
Тогда условие, соответствующее ограничению (10), будет иметь вид |
|||||||||||
|
|
d1z1 k dk zk |
1 k , |
|
|
|
(12) |
||||
а для ограничения (11) оно запишется как |
|
|
|
|
|||||||
|
|
d1z1 |
k dk zk |
1 k . |
|
|
|
(13) |
|||
Пример 1. Требуется найти компромиссное решение задачи линей- |
|||||||||||
ной оптимизации с тремя частными критериями |
|
|
|
|
|||||||
f1 1,5x1 2,8x2 max ; |
f2 |
4x1 |
4x2 min ; |
|
|
f3 8x1 3x2 max , |
|||||
область допустимых решений в которой задается ограничениями
|
7x |
12x |
2 |
|
84; |
|||
|
1 |
|
|
|
|
|
||
|
|
7x |
|
|
|
77; |
||
11x |
|
|
|
|||||
|
1 |
|
|
|
2 |
|
|
|
|
8x |
|
8x |
|
|
|
64; |
|
|
2 |
|
||||||
1 |
|
|
|
|
|
|||
|
x |
|
|
|
|
|
|
1; |
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
2 |
|||
|
|
|
|
|
|
|
||
(14) (15) (16) (17) (18)
при условии неотрицательности всех переменных.
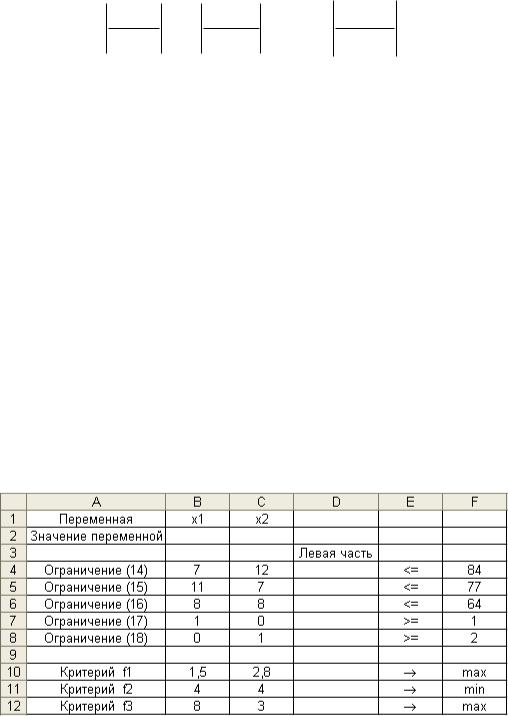
Найдем решение задачи по каждому из критериев в отдельности. Воспользуемся для этого средствами программы Excel. Исходные данные, записанные на рабочем листе электронной таблицы, показаны на рис. 1.
Рис. 1
18
Чтобы определить ограничения задачи и частные критерии оптимальности, в соответствующих ячейках требуется задать формулы, приведенные в табл. 1.
|
Таблица 1 |
|
|
Ячейка |
Формула |
D4 |
=СУММПРОИЗВ(В4:С4; $B$2:$С$2) |
D5 |
=СУММПРОИЗВ(В5:С5; $B$2:$С$2) |
D6 |
=СУММПРОИЗВ(В6:С6; $B$2:$С$2) |
D7 |
=СУММПРОИЗВ(В7:С7; $B$2:$С$2) |
D8 |
=СУММПРОИЗВ(В8:С8; $B$2:$С$2) |
D10 |
=СУММПРОИЗВ(В10:С10; $B$2:$С$2) |
D11 |
=СУММПРОИЗВ(В11:С11; $B$2:$С$2) |
D12 |
=СУММПРОИЗВ(В12:С12; $B$2:$С$2) |
Для решения задачи по каждому из критериев необходимо в диалоговом окне «Поиск решения» указать адрес целевой ячейки (D10, D11 или D12), направление оптимизации, ввести ограничения, задать параметры
(Линейная модель и Неотрицательные значения) и нажать кнопку Выполнить.
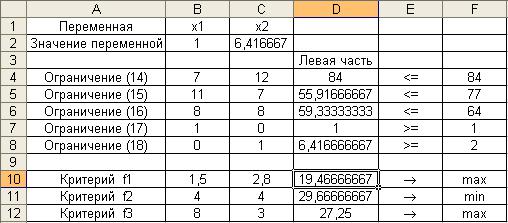
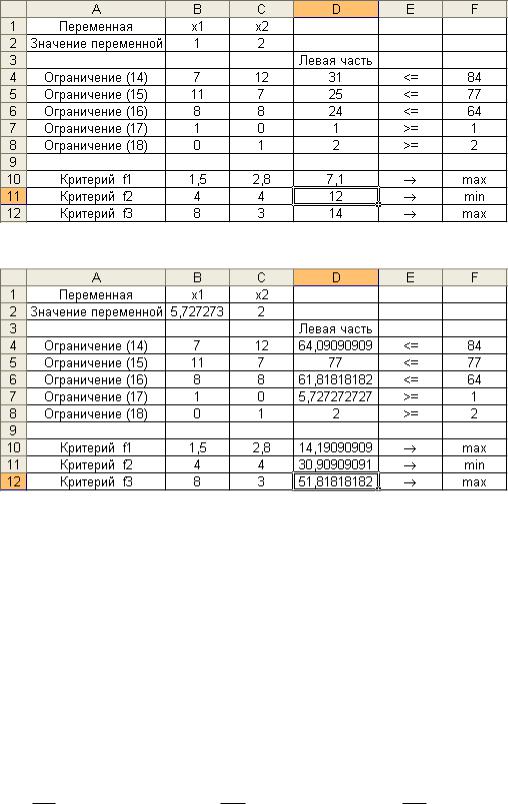
Результаты поиска решения по критерию f1 показаны на рис. 2, по критерию f2 - на рис. 3 и по критерию f3 - на рис. 4.
Рис. 2
В табл. 2 представлены значения переменных и частных критериев оптимальности, полученные при решении задачи по каждому критерию в отдельности. Очевидно, что критерии имеют противоречивый характер, так как значение каждого из них ухудшается, если решение выполняется по одному из других критериев.
19
Рис. 3
Рис. 4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Критерий |
|
|
|
Полученные результаты |
|
|
|
|
|||||||||
решения |
|
|
Переменные |
|
|
Значения критериев |
|
||||||||||
f |
|
max |
x1 |
= 1,000 |
x2 |
= 6,417 |
f *= 19,467 |
f |
2 |
= 29,667 |
f |
3 |
= 27,250 |
|
|||
1 |
|
|
1 |
|
|
|
|
|
|
|
|||||||
f |
2 |
min |
|
x1 |
= 1,000 |
x2 |
= 2,000 |
f |
|
= 7,100 |
f |
2 |
*= 12,00 |
f |
3 |
= 14,000 |
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
f |
3 |
max |
|
x1 |
= 5,727 |
x2 |
= 2,000 |
f |
= 14,191 |
f |
2 |
= 30,909 |
f |
*= 51,818 |
|
||
|
|
|
1 |
|
|
|
|
|
3 |
|
|
||||||
Далее найдем компромиссное решение задачи
наименьших отклонений. |
Поскольку все значения |
f1* |
тельны, то zk fk , причем |
zk* fk* , где k 1,2,3, и |
|
методом равных и , f2*, f3* положи-
d1 z1* 0,05137 ;
1
d |
2 |
|
|
|
1 z2*
0,08333
;
d |
3 |
|
|
|
1 z3*
0,01930
.
В качестве целевой функции расширенной задачи выберем первый частный критерий оптимальности
z1 f1 1,5x1 2,8x2 max .
Тогда дополнительные ограничения будут иметь следующий вид:
|
|
|
20 |
|
|
|
||
|
1,5x |
2,8x |
2 |
z |
0; |
|||
|
1 |
|
|
|
1 |
|
||
4x |
|
4x |
|
z |
|
0; |
||
|
2 |
2 |
||||||
1 |
|
|
|
|
||||
|
8x |
|
3x |
|
z |
|
0; |
|
|
2 |
3 |
||||||
1 |
|
|
|
|
||||
|
|
0,08333z |
|
2; |
||||
0,05137z |
|
|||||||
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
0,05137z |
0,01930z |
3 |
0. |
|||||
|
1 |
|
|
|
|
|
||
(19)
(20)
(21)
(22)
(23)
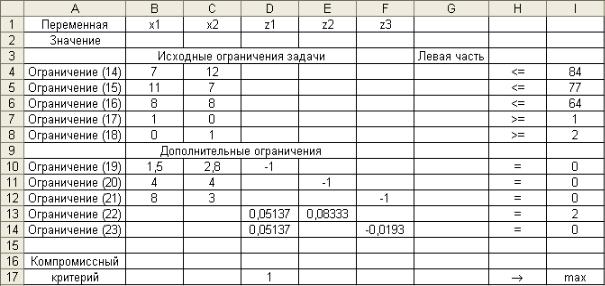
Расположение исходных данных на рабочем листе электронной таблицы показано на рис. 5.
Рис. 5
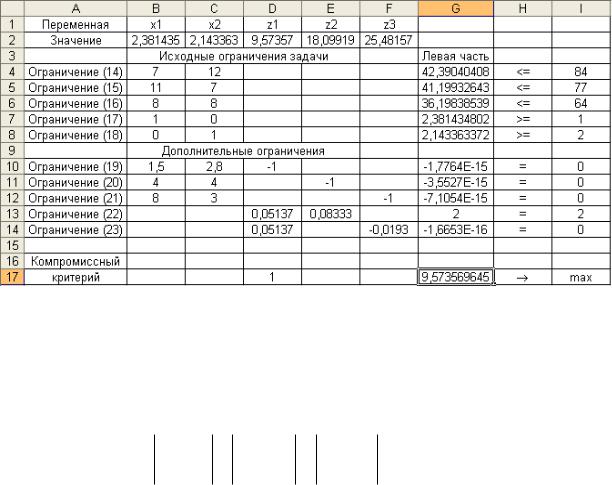
Используемые для расчетов формулы и адреса соответствующих ячеек даны в табл. 3. Значение целевой функции находится в ячейке G17, изменяемые переменные размещены в диапазоне $B$2:$F$2.
|
Таблица 3 |
|
|
Ячейка |
Формула |
|
|
G4 |
=СУММПРОИЗВ(В4:F4; $B$2:$F$2) |
G5 |
=СУММПРОИЗВ(В5:F5; $B$2:$F$2) |
G6 |
=СУММПРОИЗВ(В6:F6; $B$2:$F$2) |
G7 |
=СУММПРОИЗВ(В7:F7; $B$2:$F$2) |
G8 |
=СУММПРОИЗВ(В8:F8; $B$2:$F$2) |
G10 |
=СУММПРОИЗВ(В10:F10; $B$2:$F$2) |
G11 |
=СУММПРОИЗВ(В11:F11; $B$2:$F$2) |
G12 |
=СУММПРОИЗВ(В12:F12; $B$2:$F$2) |
G13 |
=СУММПРОИЗВ(В13:F13; $B$2:$F$2) |
G14 |
=СУММПРОИЗВ(В14:F14; $B$2:$F$2) |
G17 |
=СУММПРОИЗВ(В17:F17; $B$2:$F$2) |
21
Для получения компромиссного решения задачи в диалоговом окне «Поиск решения» указываются адрес целевой ячейки G17, направление оптимизации (для критерия z1 это максимальное значение), определяются ограничения и задаются параметры Линейная модель и Неотрицательные значения. Состояние ячеек электронной таблицы после выполнения поиска решения показано на рис. 6.
Рис. 6
Компромиссное решение, полученное по методу равных и наименьших относительных отклонений, имеет следующий вид:
x1 = 2,38; x2 = 2,14; f1 = z1 = 9,57; f2 = z2 = 18,10; f3 = z3 = 25,48.
Относительные отклонения частных критериев от их экстремальных значений удовлетворяют условию:
f1* f1 |
|
f2* f2 |
|
f3* f3 |
0,5083 . |
|
f1* |
f2* |
f3* |
||||
|
|
|
В компромиссном решении количественные значения частных критериев существенно отличаются от их экстремальных значений (табл. 2). Чтобы изменить их количественное соотношение, т.е. улучшить (ухудшить) некоторые частные критерии за счет ухудшения (улучшения) других, введем весовые коэффициенты для их относительных отклонений.
Пусть 1 = 1, 2 = 0,5 и 3 = 1. Это означает, что критерий f2 = z2 является менее важным и может быть ухудшен по сравнению с другими показателями оптимальности. Тогда для получения компромиссного решения дополнительное ограничение (22), определяющее равенство отклонений первого и второго критериев, следует заменить следующим ограничением, полученным по формуле (13):
0,05137z1 0,5 0,08333zk 1 0,5 .
Окончательно оно принимает следующий вид:
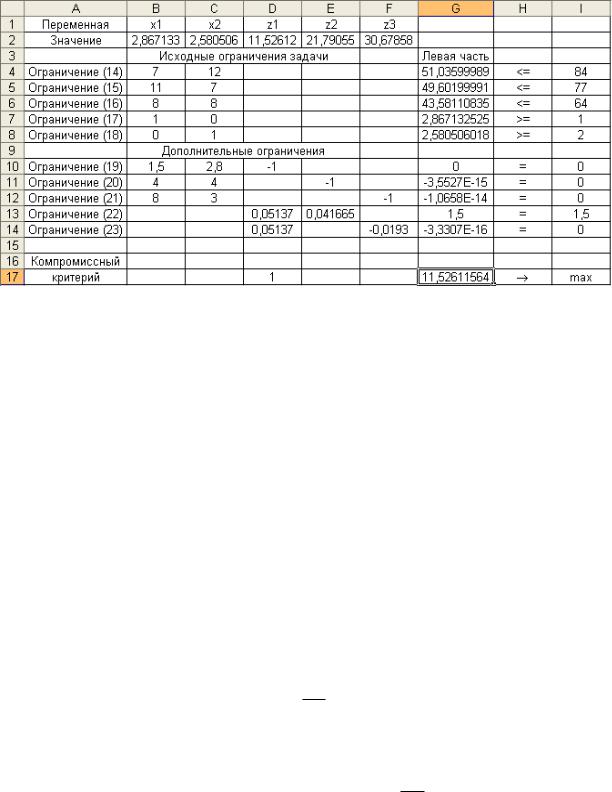
22
0,05137z |
0,041665z |
k |
1 |
|
1,5
.
Рабочий лист электронной таблицы для поиска компромиссного решения с учетом введенных весовых коэффициентов приведен на рис. 7.
Рис. 7
Полученные результаты показывают, что значения первого и третьего критериев улучшились за счет ухудшения второго критерия:
x1 = 2,87; x2 = 2,58; f1 = z1 = 11,53; f2 = z2 = 21,79; f3 = z3 = 30,69.
Замечание. Область допустимых решений задачи, определяемая ограничениями (14) - (18), представляет собой выпуклый многоугольник, расположенный в неотрицательной области координатной плоскости. Решения, полученные по каждому частному критерию в отдельности (табл. 2) соответствуют допустимым базисным решениям задачи линейного программирования и располагаются в вершинах этого многоугольника. Компромиссное решение, как правило, определяется точкой, расположенной внутри этого многоугольника.
1.2. Решение задачи многокритериальной линейной оптимизации методом минимаксного критерия
При использовании этого метода сначала также решается исходная задача (1), (2) по каждому из частных критериев в отдельности и находятся
их оптимальные значения
f |
k |
* |
|
|
,
k 1, p . Для применения минимаксного
критерия эти величины должны быть положительны. Поскольку в общем случае это условием может и не выполняться, используя соотношение (3), выполним переход к соответствующим критериям zk с положительными
экстремальными значениями zk* 0 для всех k 1, p .
