3922 / лаб2

23

Выделим из полученных отклонений наибольшее и потребуем, чтобы в искомом компромиссном решении оно было минимальным. Тогда целевая функция в общем виде запишется так:

Представим условие (25) таким образом, чтобы исключить операцию определения абсолютной величины. Очевидно, что в компромиссном решении значение максимизируемого частного критерия zs меньше его экстремального значения, т.е. zs (x) zs*. Отсюда неравенство (25) запишется

Для поиска компромиссного решения задачи многокритериальной линейной оптимизации с ограничениями (2) и частными критериями оптимальности (3) по методу минимаксного критерия требуется решить расширенную задачу линейного программирования, которая формулируется на основе исходной задачи следующим образом.

24

дачи вводится неотрицательная переменная xn+1 > 0.

Шаг 2. В качестве целевой функции принимается значение xn+1:

Z = xn+1 min. (26)

Шаг 3. В систему ограничений (2) вводятся p дополнительных неравенств, определяющих взаимосвязь отклонений частных показателей от их экстремальных значений с максимальным из этих отклонений. Вид этих неравенств зависит от направлений оптимизации частных критериев:

где F1 и F2 – подмножества максимизируемых и минимизируемых критериев соответственно.

Таким образом, компромиссное решение можно получить, если решить расширенную задачу линейного программирования с целевой функцией (26) и ограничениями (2), (27), (28) при условии неотрицательности

Пример 2. Покажем применение метода минимаксного критерия для решения задачи из примера 1, которая имеет частные критерии

и ограничения (14) - (18) при условии неотрицательности всех переменных.

Результаты решения задачи по каждому критерию в отдельности

Тогда дополнительные ограничения запишутся следующим образом:

а целевая функция (минимаксный критерий) будет иметь вид

Z x3 min .

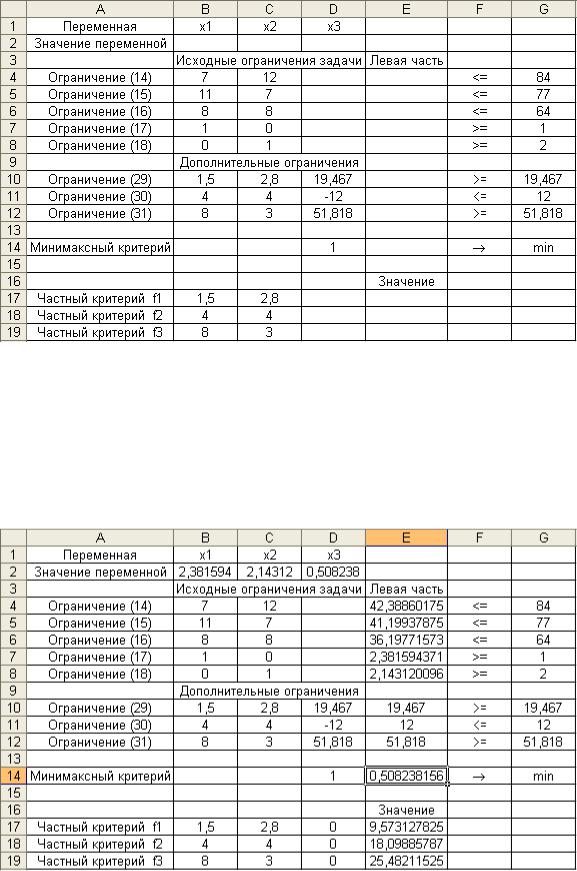
Размещение исходных данных на рабочем листе электронной таблицы для поиска компромиссного решения задачи по минимаксному критерию показано на рис. 8.

Изменяемые переменные размещены в диапазоне $B$2:$D$2. Три последние строки таблицы выполняют вычисление значений частных критериев для компромиссного решения. Результаты будут получены в ячей-

ках E17:E19.

25

Рис. 8

Для получения компромиссного решения задачи в диалоговом окне «Поиск решения» указываются адрес целевой ячейки E14, направление оптимизации (минимальное значение), определяются ограничения и задают-

ся параметры Линейная модель и Неотрицательные значения. Состоя-

ние рабочего листа электронной таблицы после завершения поиска решения показано на рис. 9.

Рис. 9

26

Компромиссное решение, полученное по минимаксному критерию, имеет следующий вид:

x1 = 2,38; x2 = 2,14; f1 = z1 = 9,57; f2 = z2 = 18,10; f3 = z3 = 25,48.

Нетрудно заметить, что оно совпадает с решением по методу равных и наименьших относительных отклонений (которые составляют 0,5083), поскольку минимаксное относительное отклонение x3 0,5082 .

2.ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1.Выбрать из табл. 4 задание на решение задачи многокритериальной линейной оптимизации, в котором f1 max, f2 max, f3 min.

2.Средствами программы Excel выполнить решение задачи по каждому частному критерию в отдельности. Результаты представить в виде табл. 2.

3.Графически построить область допустимых решений исходной задачи и указать точки, соответствующие оптимальным решениям по каждому частному критерию.

4.Составить расширенную задачу линейного программирования, необходимую для получения компромиссного решения исходной многокритериальной задачи заданным методом (равных и наименьших относительных отклонений или минимаксного критерия).

5.Средствами программы Excel получить компромиссное решение многокритериальной задачи. Указать соответствующую точку в области допустимых решений исходной задачи.

6.Задать весовые коэффициенты для частных критериев оптимальности и получить соответствующее компромиссное решение (методом равных и наименьших относительных отклонений). Проанализировать перемещение точки компромиссного решения в области допустимых решений задачи.

3. СОДЕРЖАНИЕ ОТЧЕТА

1.Цель работы.

2.Исходная задача многокритериальной линейной оптимизации.

3.Фрагмент рабочего листа электронной таблицы с исходными данными для решения задачи по каждому частному критерию (пример приведен на рис. 1).

4.Результаты решения задачи по каждому частному критерию в отдельности (пример в табл. 2).

5.Расширенная задача линейного программирования для поиска компромиссного решения соответствующим методом.

6.Фрагмент рабочего листа электронной таблицы с данными для поиска компромиссного решения (пример для метода равных и наименьших относительных отклонений приведен на рис. 5, для метода минимаксного

критерия – на рис. 8).