1.1.6. Обращение многомерной матрицы

Многомерная матрица В=А^-1называется обратной по отношению к гиперквадратной матрицеА=(р,р), если выполняются следующие соотношения:

А(р,р)В = ВА(р,р) = Е(р,р). (1.2)

Обратная многомерная матрица существует тогда и только тогда, когда определитель исходной гиперквадратной матрицы отличен от нуля. Численное обращение гиперквадратной матрицы может осуществляться путем плоского обращения ее двумерного табличного представления.

Псевдообратной многомерной матрицей В(g,p) = A⁺( g,p)по отношению к матрице А(р,g) называется матрица В, удовлетворяющая следующим аналогам условий Мура-Пенроуза :

a) A(p,g)B(g,p)A(p,g) = A(p,g);

б) B(g,p)A(p,g)B(g,p) = B(g,p);

в)[B(g,p)A(p,g)]^T = B(g,p)A(p,g);

г) [A(p,g)B(g,p)]^T = A(p,g)B(g,p).

Псевдообратная матрица всегда существует, и ее табличное представление совпадает с результатом псевдообращения двумерного табличного представления исходной матрицы. При этом выполняется условие – если обратная матрица существует, то она совпадает с псевдообратной: A⁺(p,g) = A^-1(p,g).

Таким образом, общее правило получения обратной матрицы можно записать следующим образом.

1. Обратная матрица строится на основе обращения (псевдо-обращения) ее табличного представления.

2. Индексы обратной матрицы располагаются так же, как при транспонировании матрицы. Построенная таким образом матрица определяет структуру обратной матрицы, а значения ее элементов устанавливаются по табличному представлению обратной матрицы. Примечание. Многомерные обратные матрицы могут использоваться для представления решения линейных многомерно-матричных уравнений типаА(р,р)Х(р,0)=В(р,0), которое дается соотношением:Х(р,0) =А^-1(р,р)В(р,0).

Порядок выполнения работы

1. В режиме обучения выполнить основные операции над многомерными матрицами (рис.1.1).

При выполнении можно воспользоваться подсказками (рис.1.2), результаты выполнения контролируются программой. Желательно на этапе обучения добиться безошибочного выполнения заданий путем многократного выполнения операций.

2. В режиме контроля выполнить основные операции над многомерными матрицами и оформить отчет о выполненной работе.

Содержание отчета

1. Краткое описание основных операций над многомерными матрицами.

2. Результаты выполнения работы в режиме контроля.

3. Выводы. Рекомендации по формированию пояснений на обучающем стенде в соответствии с результатами программного контроля (рис. 1.3).

Р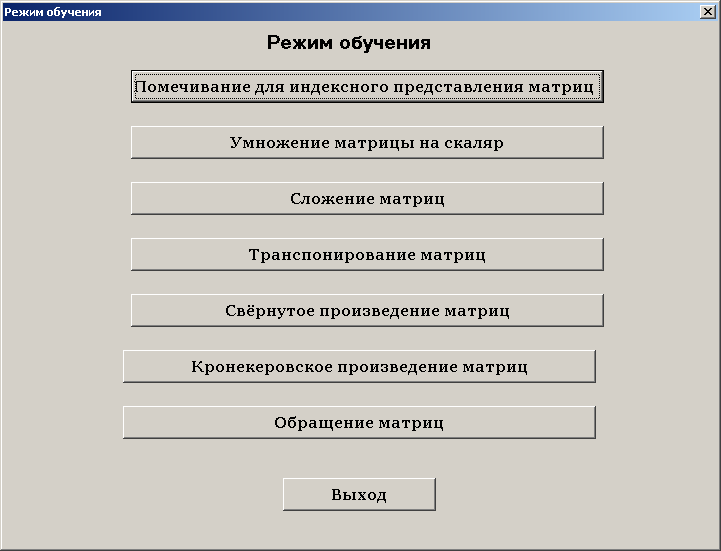ис. 1.1. Обучающий стенд

Рис. 1.2. Обучающий стенд. Пример пояснения правила выполнения операции

Р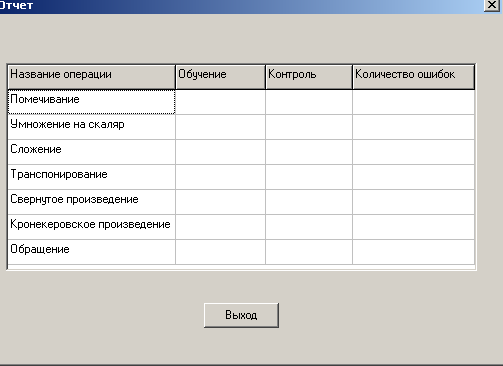ис. 1.3. Результаты программного контроля выполнения работы

2. Основные определения теории графов

2.1. Понятие о графе. Способы задания графа [4,5].

2.1.1. Задание графа множествами вершин и линий

Граф геометрически представляет собой множество точек, соединенных линиями. Для более полного математического определения графа введем ряд обозначений. Множество точек или вершин х₁,х₂,…х_nграфаGобозначим черезХ, а множество линийd₁,d₂,…d_m, соединяющих между собой эти вершины – символомА. Тогда графGможно полностью задать парой(Х,А).

Если соединяющиеся линии из множества Аориентированы, что обычно показывается стрелкой, то они называются дугами и граф с такими линиями называется ориентированным графом. Если соединяющие линии не ориентированы, то они называются ребрами, а граф называется неориентированным. В смешанном графе могут быть дуги (ориентированные линии) и ребра (неориентированные линии). На рис. 2.1 изображен ориентированный граф.

Дуга такого графа задается упорядоченной парой, состоящей из начальной и конечной вершин, ее направление предполагается заданным от первой вершины ко второй. Для подчеркивания ориентации ребра упорядоченная пара обозначается сверху Рис. 2.1 символом вектора, например знаком®.

Граф на рис. 2.1. можно представить в виде

G₁={ x₁, x₂, x₃; (x₁,x₂), (x₂,x₃), (x₃,x₁)}

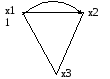
На рис. 2.2 изображен смешанный граф, и его представление имеет вид

G₂={ x₁, x₂, x₃; 2(x₁,x₂), (x₂,x₃), (x₃,x₁)} ,

где цифра 2 означает две дуги из вершины х₁в вершину х₂.

Рис. 2.2