Порядок выполнения работы

1. В режиме обучения проследить отображаемый на экране дисплея поэтапный процесс решения задачи о назначениях (рис. 6.2).

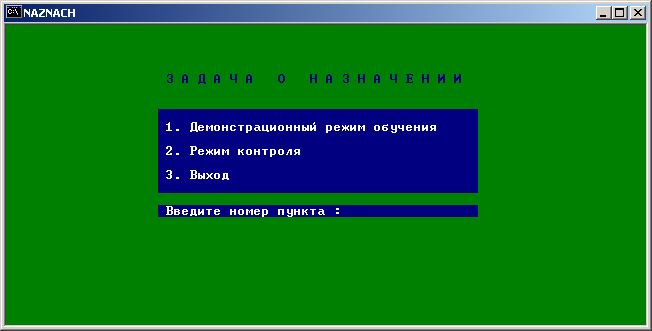
Рис. 6.2. Решение задачи о назначениях

2. В режиме контроля решить задачу о назначениях с помощью меню операций (рис. 6.3).

Рис.6.3. Меню операций

Содержание отчета

1. Краткое описание алгоритма.

2. Матрица эффективностей.

3. Матрица назначений.

4. Выводы. Рекомендации по формированию пояснений на обучающем стенде в соответствии с результатами программного контроля.

Лабораторная работа № 7

Задача коммивояжера

^{Цель работы}

^{Теоретическое и практическое изучение алгоритма решения задачи коммивояжера методом ветвей и границ с помощью задачи о назначениях.}

^{Теоретическая часть}

Задана матрица расстояний между вершинами графа. Коммивояжер должен объехать все города (вершины графа), посетив каждый из них только один раз. Цикл обхода минимальной длины называется оптимальным гамильтоновым циклом. Для его нахождения применим метод ветвей и границ. Решаем задачу о назначениях для заданной матрицы расстояний между вершинами графа. Назначения будут соответствовать последовательности обхода городов. Циклы малой длины следует разрывать, придавая весам дуг значения, равные бесконечности.

Рассмотрим пример решения задачи коммивояжера.

Пусть задана матрица весов (расстояний) c_ij :

	j=1	j=2	j=3	j=4	j=5	j=6
i=1	∞	4	10	18	5	10
i=2	4	∞	12	8	2	6
i=3	10	12	∞	4	18	16
i=4	18	8	4	∞	14	6
i=5	5	2	18	14	∞	16
i=6	10	6	16	6	16	∞

Нужно сделать такой обход, чтобы все вершины были пройдены, но время обхода было минимально. Для этого решаем задачу о назначениях, а затем разрываем цепь с наименьшим количеством дуг. Для этого вес соответствующей дуги делаем равным ∞.

Решаем задачу о назначениях :

	j=1	j=2	j=3	j=4	j=5	j=6
i=1					0*
i=2						0*
i=3				0*
i=4			0*
i=5	0*
i=6		0*

Время ”обхода” I=30 ;порядок обхода (рис.7.1).

2

1

3

6

5

4

Рис. 7.1. Порядок обхода вершин графа

Разрываем цепь с наименьшем количеством дуг(вес соответствующей дуги становится равным ∞). Дерево решений представлено на рис. 7.2.

P₀=30

C₁₅=∞

C₅₁=∞

P₁=31

P₂=31

C₄₃=∞

C₃₄=∞

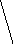
C₄₃=∞

C₃₄=∞

P₄=33

Гамиль-тонов

цикл

P₃=34

P₅=33

Гамиль-тонов

цикл

P₆=34

Рис. 7.2. Дерево решений

Порядок выполнения работы

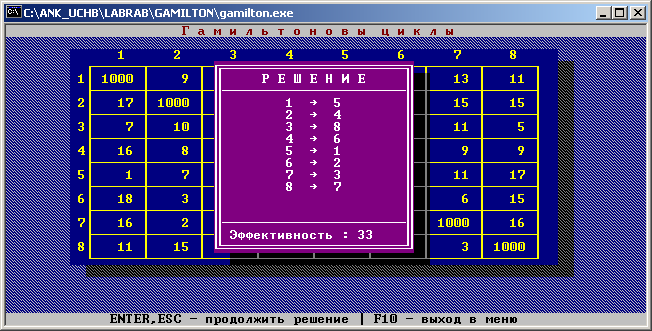
1. Для заданного варианта с помощью программы ”Назначения” сформировать для отчета дерево решений. Пример представления решения задачи о назначениях показан на рис. 7.3.

Рис. 7.3. Представление решения задачи о назначениях

2. Для каждого шага ветвления нарисовать получающиеся в результате решения циклы.

Содержание отчета

1. Краткое описание задачи о назначениях, метода ветвей и границ, задачи коммивояжера.

2. Показать по дереву решения нецелесообразность дальнейшего ветвления задачи.

3. Выводы. Рекомендации по формированию пояснений на обучающем стенде в соответствии с результатами выполнения работы.

Лабораторная работа № 8

Задача о наименьшем покрытии

^{Цель работы}

^{Теоретическое и практическое изучение алгоритма решения задачи о наименьшем покрытии методом ветвей и границ.}

^{Теоретическая часть}

8.1. Постановка задачи

В матричной форме задача о покрытии формулируется следующим образом. Дана матрица A(N,M) с элементами из множества {0,1}. При этом считают, что номера строк образуют покрываемое множество, а номера столбцов - покрывающее. Требуется найти подматрицу матрицы A, которая содержит N строк (среди которых нет нулевых) и состоит из минимально возможного числа столбцов. К подобной формулировке могут быть сведены многие оптимизационные задачи управления.

8.2. Алгоритм решения задачи

Задача о покрытии является достаточно сложной комбинаторной задачей и на ЭВМ она чаще всего решается в два этапа. На предварительном этапе выясняется, имеет ли вообще исходная задача решение, и если оно существует, то определяется приближенное решение. Здесь же могут быть найдены элементы покрывающего множества (столбцы), включаемые в оптимальное решение, что позволяет упростить исходную задачу.

8.2.1.Упрощение задачи

1. Если в какой-либо строке отсутствует единица, то этот элемент не может быть покрыт, задача не имеет решения.

2. Если в строке присутствует только одна единица, то соответствующий столбец обязательно включают в решение, он исключается из перебора задачи вместе с элементами множества, которое он покрывает.

3. Пусть есть строки: первая – подмножество второй. Тогда исключается более мощная строка.

4. Имеем два столбца: один – подмножество другого. Исключаем столбец с наименьшим количеством единиц.