4.4. Порядок выполнения работы
1. В демонстрационном режиме (программа OR_WORK) построить выпуклую область дискретного конечного множества элементов.
2. Открыть файл obras.exe, система меню которого ориентирована на реализацию всех этапов построения области работоспособности.
3. В демонстрационном режиме (программа Преобразование. exe) произвести преобразования области.
Содержание отчета
1. Краткое описание алгоритма.
2. Координаты исходных точек
3. Графическое представление области.
4. Представление преобразованной области множеством элементов и системой неравенств.
Лабораторная работа № 5
Решение задачи о максимальном потоке
в табличной форме
Цель работы
Теоретическое и практическое изучение алгоритма решения задачи о максимальном потоке между начальной и конечной вершинами графа.
Теоретическая часть
Рассмотрим решение задачи для случая определения максимального потока в многоуровневом графе. Решение приводится на основе использования многомерных матриц (лабораторная работа № 1). Условие задачи зададим с помощью многомерной матрицы
,
где
- номера начального и конечного уровней;
- номера начальной и конечной вершин
графа;
- пропускные способности дуг из вершиныj+(уровня
)
в вершину
(уровня
).
5.1. Общий шаг алгоритма
Общий шаг состоит из трех действий.
1. Помечаем столбец, соответствующий
вершине-источнику
,
знаком *. Затем отыскиваем в строке
все положительные
.
Содержащие их столбцы помечаем сверху
числом, соответствующим номеру источника
.
Далее переходим к просмотру тех строк,
которые имеют те же номера, что и
отмеченные столбцы. В каждой строке
отыскиваем все положительные
,
расположенные в непомеченных столбцах,
и отмечаем эти столбцы номером
просматриваемой строки
.
Процесс оканчивается: а) когда помечен
сток; б) когда все строки просмотрены и
нельзя отметить новые столбцы. В случае
«а» новый путь из источника в сток
находим, начиная от стока по отметкам
столбцов. Последняя вершина пути – сток
.
По отметке, например
над столбцом
,находим
предшествующую
вершину
.
Число
отметим знаком минус
,
а число
- знаком плюс
.
Пусть столбец
был помечен номером
.
Двигаемся от числа
по столбцу до строки
.
Продолжаем этот процесс до тех пор, пока
не придем к источнику *.
В случае «б» алгоритм поиска нового пути закончен.
2. Определяем величину, на которую можно
увеличить поток на найденном пути, e
= min
{
}.
3. Вычисляем новые пропускные способности
дуг. Для этого из всех
вычитаемe,
а ко всем
прибавляемe.
Получаем новую матрицу пропускных
способностей. Затем стираем в таблице
все пометки и возвращаемся к действию
1.
Для определения полученного максимального потока вычитаем из всех элементов первоначальной матрицы R(2,2)соответствующие элементы матрицы, полученной на последнем шаге. Положительные значения найденных разностей дают величиныпотоков по дугам многомерного графа.
Данное обобщение метода Форда-Фалкерсона на многомерный случай позволяет использовать алгоритм для решения многих задач, сводящихся к потоковым.
5.2. Пример решения задачи о максимальном потоке
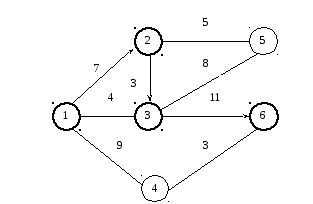
Рис. 5.1. Исходный граф с проставленными весами ребер
Рассмотрим задачу на примере одноуровневого графа (рис.5.1). Необходимо найти максимальный поток, зная пропускные способности связей. Примем S=1 – начальная точка,t=6 – конечная точка.
Составим таблицу пропускных способностей графа(табл. 5.1).
Таблица 5.1
-
y=1
y=2
y=3
y=4
y=5
y=6
i=1
0
7
4
9
0
0
i=2
7
0
3
0
5
0
i=3
4
3
0
0
8
11
i=4
9
0
0
0
0
3
i=5
0
5
8
0
0
0
i=6
0
0
11
3
0
0
Алгоритм решения задачи о максимальном потоке состоит в следующем:
1) определить путь из Sвt;
2) определить величину потока, на которую изменим все интенсивности потока- ε;
3) определить новые интенсивности потока.
Шаг 1.
Помечаем начальный столбец *, входим в строку с номером столбца(*), помечаем все столбцы, содержащие положительные элементы строки, номером этой строки.
Войдем в строки с номерами помеченных столбцов, помечаем все столбцы, содержащие положительные элементы строк, номерами соответствующей строки и так до тех пор, пока не дойдем до конечного столбца(t), где соответствующий элемент помечается знаком «-», а элемент таблицы с транспонированными значениями отмечаем знаком «+».
Входим в столбец с элементом с транспонированными значениями индексов, двигаемся по нему до строки с номером над столбцом и помечаем его «-», элемент с транспонированными значениями – «+».Так до тех пор, пока не придем к начальному столбцу.
Среди элементов со знаком «-» ищется минимальный, на эту величину изменяем интенсивность потоков по правилу: если элемент обозначен «-», то вычитаем из него ε, если «+» - добавляем ε.
Подобные преобразования делаются до тех пор, пока можно пройти из начальной в конечную вершину.
Шаг 2.
Из начальной матрицы вычитается конечная матрица. При этом оставляем лишь положительные элементы.
Шаг 1 (табл. 5.2, 5.3, 5.4).
Таблица 5.2
* 1 2 1 2 4
-
y=1
y=2
y=3
y=4
y=5
y=6
i=1
0
7
4
9ˉ
0
0
i=2
7
0
3
0
5
0
i=3
4
3
0
0
8
11
i=4
9+
0
0
0
0
3ˉ
i=5
0
5
8
0
0
0
i=6
0
0
11
3+
0
0
ε=3 , на основе вычислений 4. шага 1-го, получаем
Таблица 5.3
* 1 2 1 2 3
-
Y=1
y=2
y=3
y=4
y=5
y=6
i=1
0
7ˉ
0
6
0
0
i=2
7+
0
3ˉ
0
5
0
i=3
8
3+
0
0
8
7ˉ
i=4
12
0
0
0
0
0
i=5
0
5
8
0
0
0
i=6
0
0
15+
6
0
0
ε=3, на основе вычислений 4. шага 1-го, получаем
Таблица 5.4
*
-
Y=1
y=2
y=3
y=4
y=5
y=6
i=1
0
4ˉ
0
6
0
0
i=2
10+
0
0
0
5ˉ
0
i=3
8
6
0
0
8+
4ˉ
i=4
12
0
0
0
0
0
i=5
0
5+
8ˉ
0
0
0
i=6
0
0
18+
6
0
0
ε=4и т.д.
Шаг 2:окончательная матрица
-
y=1
y=2
y=3
y=4
y=5
y=6
i=1
0
7
4
3
0
0
i=2
0
0
3
0
4
0
i=3
0
0
0
0
0
11
i=4
0
0
0
0
0
3
i=5
0
0
4
0
0
0
i=6
0
0
0
0
0
0