4.3. Алгоритм преобразования области в плоскостных координатах

Пусть M - произвольная точка на плоскости с координатами и , вычисленными относительно заданной прямолинейной координатной системы. Однородными координатами этой точки называется любая тройка одновременно не равных нулю чисел , связанных с заданными числами и следующими соотношениями:

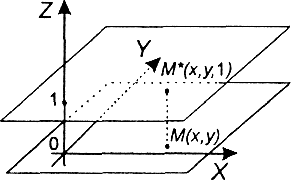
Рис. 4.6. Преобразование координат точки на плоскости в однородные координаты

При решении задач компьютерной графики однородные координаты обычно вводятся так: произвольной точке на плоскости ставится в соответствие точка в пространстве (рис. 4. 6).

Заметим, что произвольная точка на прямой, соединяющей начало координат, точку , с точкой , может быть задана тройкой чисел вида . Будем считать, что не равно 0.

Вектор с координатами является направляющим вектором прямой, соединяющей точки и . Эта прямая пересекает плоскость в точке , которая однозначно определяет точку координатной плоскости .

Тем самым между произвольной точкой с координатами и множеством троек чисел вида , при не равной 0, устанавливается (взаимно однозначное) соответствие, позволяющее считать числа новыми координатами этой точки.

В проективной геометрии для однородных координат принято следующее обозначение: или, более общее, (напомним, что здесь непременно требуется, чтобы числа одновременно в нуль не обращались).

Применение однородных координат оказывается удобным уже при решении простейших задач.

Рассмотрим, например, вопросы, связанные с изменением масштаба. Если устройство отображения работает только с целыми числами (или если необходимо работать только с целыми числами), то для произвольного значения (например, ) точку с однородными координатами представить нельзя. Однако при разумном выборе можно добиться того, чтобы координаты этой точки были целыми числами. В частности, при для рассматриваемого примера имеем .

Рассмотрим другой случай. Чтобы результаты преобразования не приводили к арифметическому переполнению, для точки с координатами можно взять, например,. В результате получим .

Приведенные примеры показывают полезность использования однородных координат при проведении расчетов. Однако основной целью введения однородных координат в дискретной математике является их несомненное удобство в применении к геометрическимпреобразованиям.

С помощью троек однородных координат и матриц третьего порядка можно описать любое аффинное преобразование плоскости.

В самом деле, считая , сравниваем две записи: помеченную символом * и нижеследующую, матричную:

.

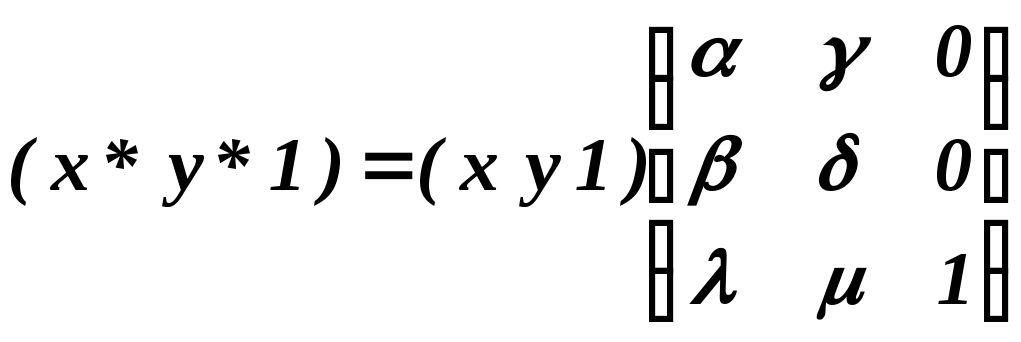Нетрудно заметить, что после перемножения выражений, стоящих в правой части последнего соотношения, мы получим обе формулы (*) и верное числовое равенство .

Тем самым сравниваемые записи можно считать равносильными.

Элементы произвольной матрицы аффинного преобразования не несут в себе явно выраженного геометрического смысла. Поэтому чтобы реализовать то или иное отображение, т.е. найти элементы соответствующей матрицы по заданному геометрическому описанию, необходимы специальные приемы. Обычно построение этой матрицы в соответствии со сложностью рассматриваемой задачи и с описанными выше частными случаями разбивают на несколько этапов.

На каждом этапе ищется матрица, соответствующая тому или иному из выделенных выше случаев А, Б, В и Г, обладающих хорошо выраженными геометрическими свойствами.

Выпишем соответствующие матрицы третьего порядка.

А. Матрица вращения (rotation)

.

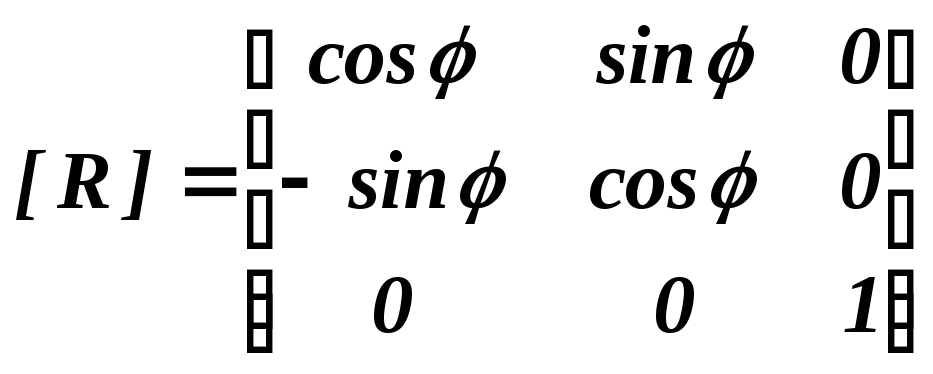Б. Матрица растяжения (сжатия) (dilatation)

.

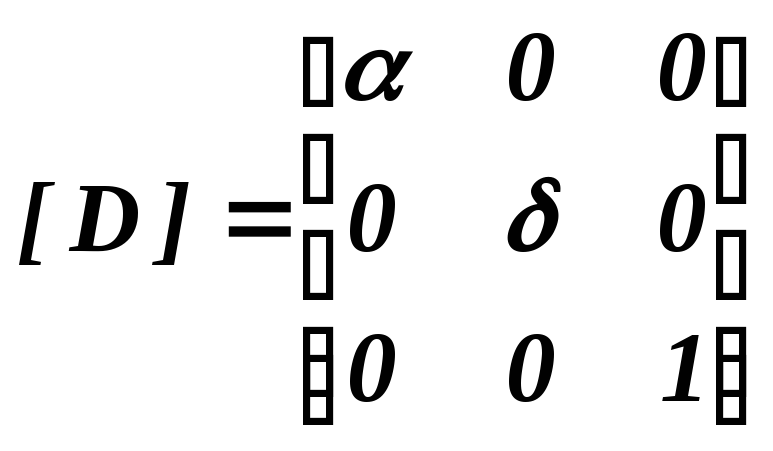В. Матрица отражения (reflection)

.

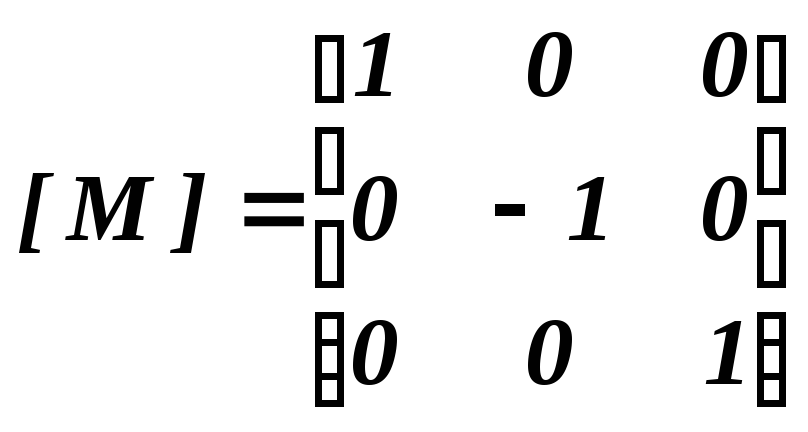Г. Матрица переноса (translation)

.

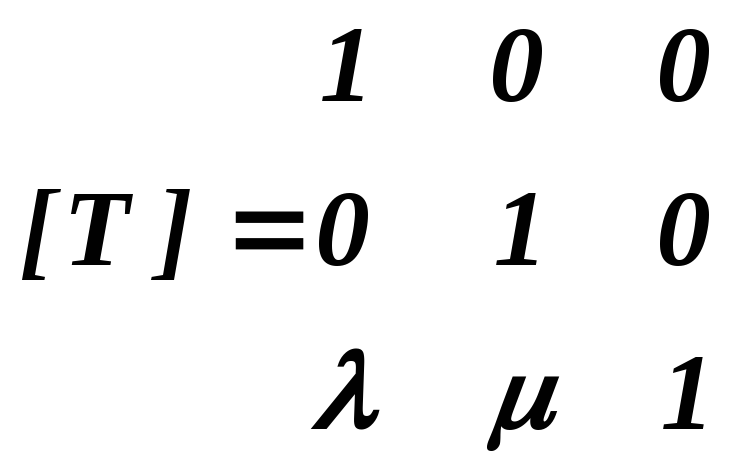Эти матрицы трактуются как составляющие общей матрицы, преобразующей исходную матрицу графического объекта в матрицу преобразованного объекта.

Общая матрица преобразования при известных иполучается перемножением матриц простейших преобразований .

Демонстрационный пример (файлПреобразование.exe)

Рассмотрим фигуру, состоящую из 8 точек, координаты которых представлены в табл. 4.3. На рис. 4.7 отображен процесс ввода данных точек.

Таблица 4.3

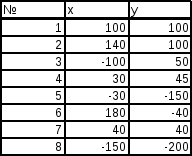
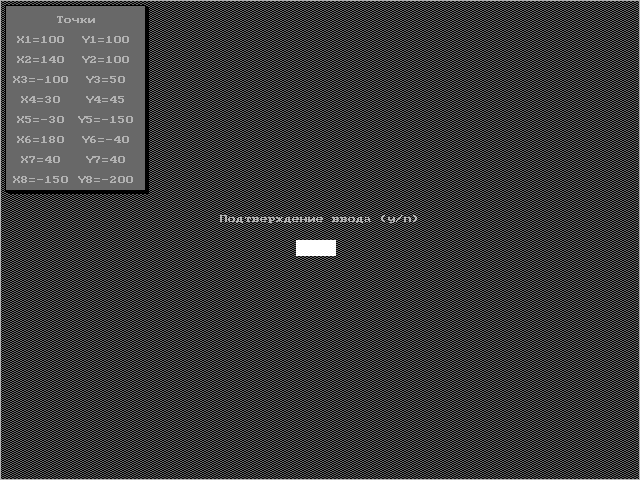
Рис. 4. 7. Ввод координат точек

На рис. 4.8 изображены исходные точки. После аппроксимации генерируется выпуклая фигура (рис. 4.9), над которой осуществляются следующие преобразования:

• поворот на 90 градусов (рис.4.10);

• растяжение с коэффициентом увеличения по осям и0,5 и 0,7 соответственно (рис. 4.11);

• перенос фигуры влево на 30 и вверх на 60 (рис. 4.12);

• отражение фигуры относительно оси y(рис. 4.13).

На рис. 4.14 отображен окончательный результат пересчета координат всех точек.

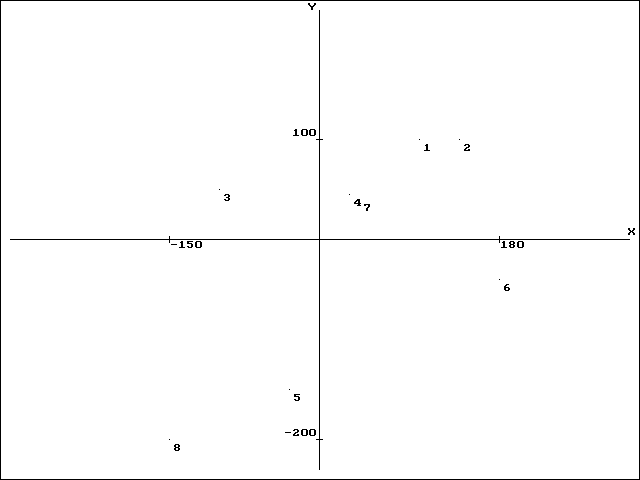
Рис. 4.8. Исходная совокупность точек

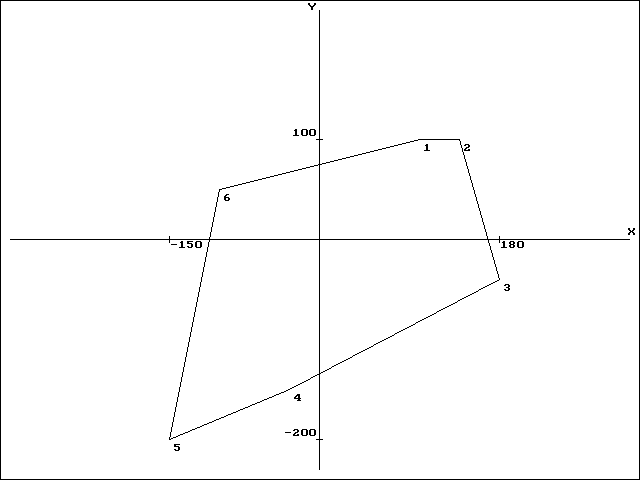
Рис. 4.9. Аппроксимированная область

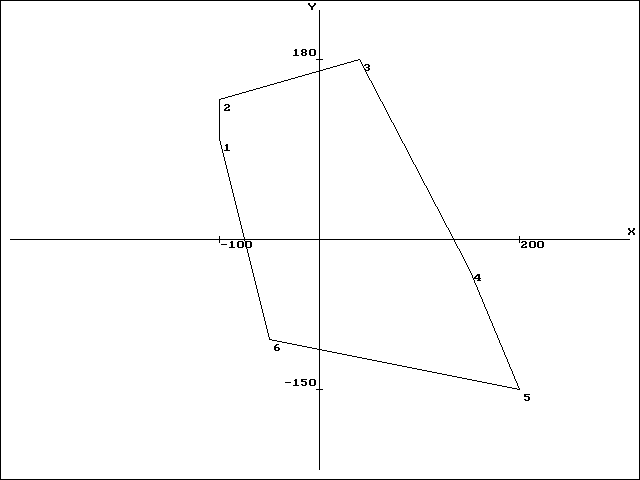
Рис. 4.10. Область после операции «Поворот»

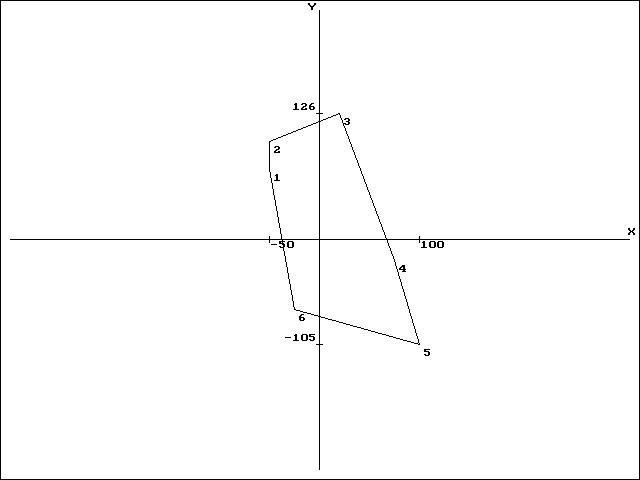
Рис. 4.11. Область после операции «Растяжение/Сжатие»

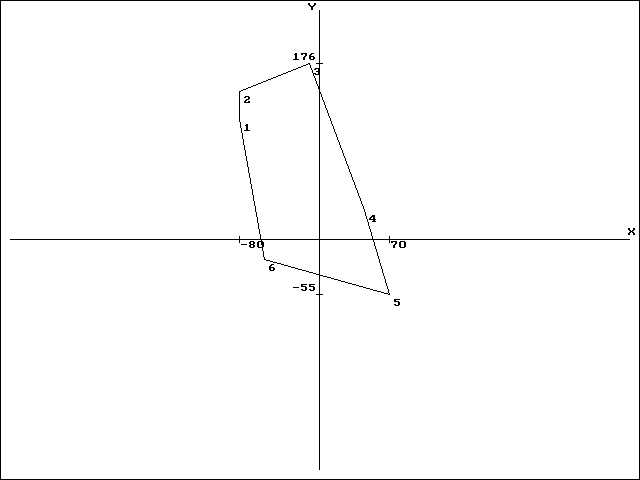
Рис. 4.12. Область после операции «Перенос»

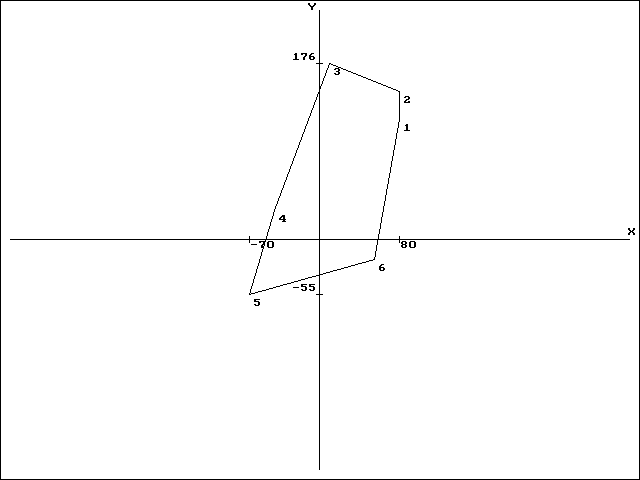
Рис. 4.13. Область после операции «Отражение»

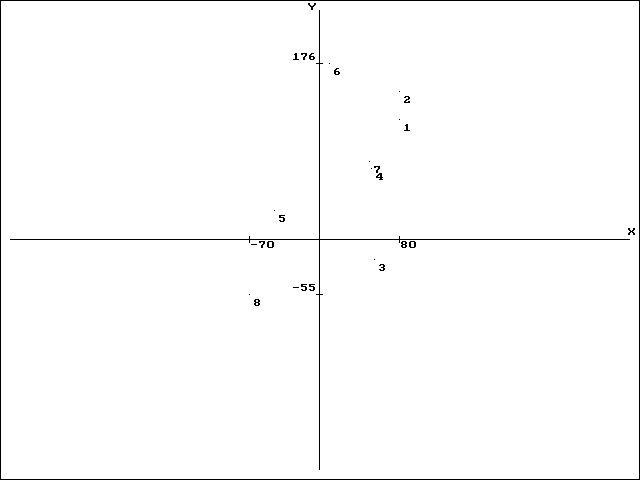
Рис. 4.14. Результирующая (преобразованная) совокупность точек

Наличие точных математических моделей объектов позволяет относительно легко отображать их на экране монитора, а вычисленные матрицы преобразований дают возможность манипуляции этими объектами на экране и позволяют повысить наглядность представления выпуклой области дискретного конечного множества элементов.