Порядок выполнения работы

1. Пройти режим обучения нахождения минимального остовного дерева в графе (программа ”Остов”) с помощью алгоритма Краскала.

2. Для заданного варианта выполнить в режиме контроля построение минимального остовного дерева в графе (программа ”Derevo”) с помощью алгоритма Краскала.

3. Пройти режим обучения нахождения минимального остовного дерева в графе (программа ”Остов”) с помощью алгоритма Прима.

4. Для заданного варианта выполнить в режиме контроля построение минимального остовного дерева в графе (программа ”Derevo”) с помощью алгоритма Прима.

Содержание отчета

1. Краткое описание алгоритма.

2. Матрица весов.

3. Графическое представление графа кратчайшего остовного дерева.

4. Выводы. Рекомендации по формированию пояснений на обучающем стенде в соответствии с результатами программного контроля.

Лабораторная работа № 4

Метод гиперплоскостей для построения выпуклой области дискретного конечного множества элементов

^{Цель работы}

^{Теоретическое и практическое изучение алгоритма описания конечного множества элементов.}

^{4.1. Теоретическая часть}

Метод гиперплоскостей заключается в последовательном включении каждой граничной точки в выпуклую оболочку и в исключении гипер­плоскостей, оказавшихся внутри области.

Вычислительная процедура построения области работоспособности по граничным точкам методом гиперплоскостей заключается в выполне­нии следующих операций.

1

Рис.4.1. Построение области

работоспособности

по граничным точкам

. Выбираются произвольным образом первые (N + I) граничные точки (на рис. 4.1 для N = 2 точки 1, 2, 3) и строятся по ним (N + 1) гиперплоскости (для N = 2 прямые 1-2, 2-3, 3-1). Для каждой построенной гиперплоскости запоминаются координаты граничных точек, по которым она построена, и координаты ее вершины.

Вершиной данной гиперплоскости условимся называть ту точку из выбранных (N + 1) точек, через которую не проводится гиперплоскость (на рис. 4.1 точки 1 и 2 являются соответственно вершинами гиперплоскостей 2-3 и 1-3).

2.Определяется для следующей, выбранной произвольно, граничной точки (точка 4) соответствующая ей генеральная гиперплоскость (прямая 1-3). Генеральной гиперплоскостью данной граничной точки будем называть гиперплоскость, вершина которой и данная граничная точка расположены по разные от нее стороны.

Генеральных гиперплоскостей для данной граничной точки может быть несколько (для точки 5 прямые 1-4, 3-4), особенно при построении многомерных областей работоспособности. Поэтому поиск генеральной гиперплоскости осуществляется среди всех ранее построенных гипер­плоскостей.

Отсутствие генеральной гиперплоскости для граничной точки означает, что точка находится внутри области, образованной ранее проведенными гиперплоскостями. Наличие таких точек свидетельствует о невыпуклости множества точек, соответствующих работоспособным состояниям объекта.

3.Выполняется п.1 для данной граничной точки и точек, че­рез которые была ранее проведена ее генеральная плоскость, найден­ная в п.2. Затем в памяти ЭВМ стираются значения коэффициентов ге­неральной гиперплоскости, координаты ее вершины и точек, через ко­торые она проведена. В противном случае область может быть построена неверно, так как генеральная гиперплоскость пересекает ее, а также может быть принята за генеральную гиперплоскость для последующих граничных точек.

Аналогичные действия выполняются для каждой генеральной гипер­плоскости, если их для данной граничной точки несколько. При этом среди вновь проведенных гиперплоскостей будут одинаковые (на рис. 4.1 через точки 4 и 5 дважды проводится прямая 4-5), информация о кото­рых должна стираться в памяти ЭВМ по тем же причинам, что и для генеральных гиперплоскостей.

4.Выбирается следующая по порядку граничная точка, и все по­вторяется с п.2.

После перебора всех граничных точек процесс построения области работоспособности заканчивается и производится определение знаков “”, “” для системы линейных неравенств).

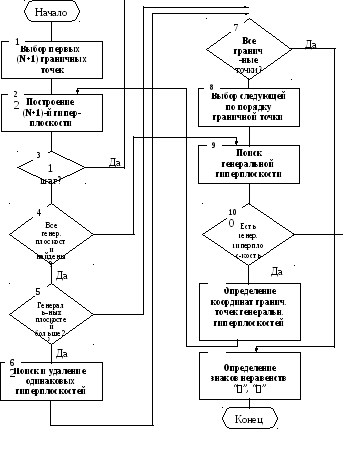
Блок-схема алгоритма построения области работоспособности по граничным точкам приведена на рис.4.2.

Блок 1

Производится выбор первых (N + 1)граничных точек из массива всех граничных точек.

Блок 2

Процедура построения гиперплоскости через заданные N гранич­ных точек занимает центральное место в данном алгоритме. Коэффи­циенты гиперплоскости (неравенства) определяются в результате ре­шения системы линейных алгебраических уравнений (N + 1)-го порядка. Систему получают в результате составления уравнений гипер­плоскостей, записав вместо переменных координаты N точек, через которые необходимо провести гиперплоскость:

(4.1)

.

Так как количество неизвестных коэффициентов (N + I), то необходимо одному из них задать произвольное значение, например a = 1, Однако в этом случае невозможно построить гиперплоскость, параллельную оси координат X.

Аналогично, если присвоить значение другому коэффициенту b = 1 системы уравнений (4.1), то предлагаемый подход будет неприменим для построе­ния гиперплоскостей, параллельных соответствующим осям координат, а при задании k  0 - для построения гиперплоскостей, проходящих через начало координат.

Нет

Нет

Нет

Нет

11

Нет

12

Рис. 4.2. Блок-схема алгоритма построения выпуклой области дискретного конечного множества элементов

С целью устранения второго недостатка вводятся (N + 1)-я пере­менная z и дополнительная точка (точка 4 на рис.4.3). Тогда построе­ние гиперплоскости осуществляется в (N + 1)-м пространстве, а произвольное значение присваивается коэффициенту при переменной z. Координаты дополнительной точки (точка 4) необходимо выбирать такими, чтобы ни одна из гиперплоскостей не была параллельна оси координат (N + 1)-й переменной z. Это требование выполняется, если значение хотя бы одной из координат дополнительной точки (не считая координаты по оси z) меньше минимального или больше макси­мального значения соответствующей координаты множества граничных точек. Значения остальных координат задаются произвольно.

В результате решения системы (N + 1)-го порядка (4.1) определяются значения коэффициентов (N + 1)-й гиперплоскости. Исключение из уравнений гиперплоскостей дополнительной переменной позволяет получить область в N-мерном пространстве (заштрихованная область на рис. 4.3).

Блоки 3, 4

Производится проверка - первые ли (N + 1) гиперплоскостей построены. Если первые, то осуществляется поиск генеральной гипер­плоскости. В противном случае выполняется проверка - все ли генеральные гиперплоскости найдены и использованы при построении гиперплоскостей для данной граничной точки.

Блоки 5, 6

После построения всех гиперплоскостей для данной граничной точки внутри области работоспособности оказываются генеральная гиперплоскость и одна или несколько пар одинаковых гиперплоскос­тей, если генеральных гиперплоскостей больше одной (рис. 4.2).

К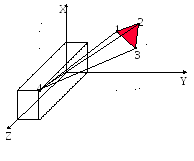ак указывалось ранее, при дальнейшем построении выпуклой оболочки эти гиперплоскости могут быть приняты за генеральные для последующих граничных точек, что приведет к неправильному построению области работоспособности. Поэтому при переходе к следующей граничной точке значения их коэффициентов необходимо исключить.

Рис. 4.3. Введение дополнительной точки

Блоки 7, 8

Проверяется наличие граничных точек. Если есть граничные точки, которые еще не включены в выпуклую оболочку, то выбирает­ся следующая точка из массива граничных точек и процесс построения области работоспособности продолжается далее.

Блок 9

Поиск генеральной гиперплоскости осуществляется среди всех ранее построенных гиперплоскостей в результате подстановки в урав­нение каждой гиперплоскости координат ее вершины и данной гранич­ной точки. Признаком генеральной гиперплоскости является противо­положность знаков результатов подстановки.

Блок 10

Проверяется наличие для выбранной граничной точки хотя бы одной генеральной гиперплоскости. Отсутствие генеральной гипер­плоскости для данной граничной точки свидетельствует о том, что точка оказалась внутри области работоспособности и данная точка может быть исключена.

Блок 11

Для найденной генеральной гиперплоскости производится поиск координат N точек, по которым она была построена.

Блок 12

Знаки неравенств “” и " " определяются в результате подстановки координат вершин гиперплоскости в уравнение гиперплоскости. При этом используется свойство вершин принадлежать области работоспособности. Символ "” соответствует отрицательному знаку результата подстановки, символ “” - положительному. Для удобства использования результатов построения области работоспособности все неравенства приводятся к виду “0”.

Диалоговое меню

Система меню ориентирована на реализацию всех этапов построения области работоспособности.

1 - вычисление величины критерия по параметрам T и  (вычисляется критерий при заданных пользователем T,  ).

2 – построение прямой через две заданные точки (на печать выводятся коэффициенты А,В,СпрямойAT + B + C = 0).

3 – построение области работоспособности [по граничным точкам, заданным в строгой последовательности их расположения вдоль границы (направление обхода граничных точек не играет роли), строится система граничных прямых в координатах: T - ось координат,  - ось абсцисс].

4 - вычисление линейной формы (вычисление левой части уравнения прямой AT+ B + C  Sпри заданных пользователемT,).

5 - построение графика переходного процесса (строится график переходного процесса объекта контроля h(t), где вертикальными линиями отмечаются допустимые значения критерия качества - минималь­ное и максимальное время регулирования tp_min, tp_max).

6 - справочная информация (содержит рекомендации по выполнению лабораторной роботы).

7 - конец работы.