Posit1nov (1)

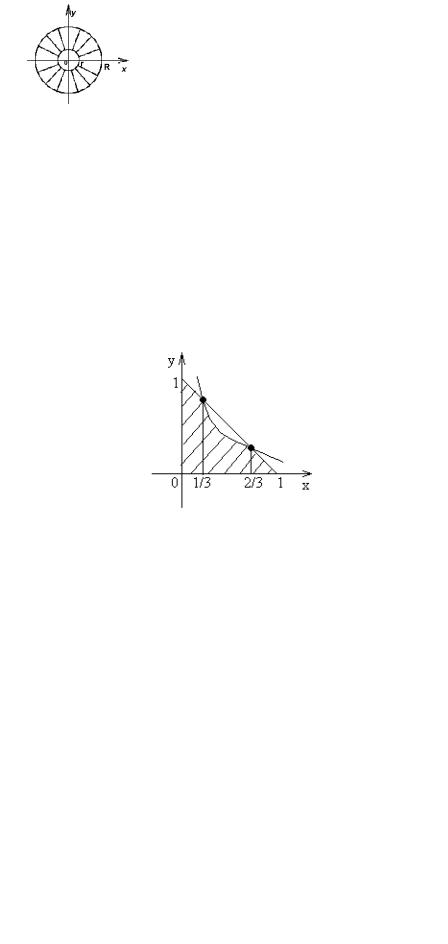
Геометрические вероятности обладают всеми свойствами, доказанными в предложении 2.1 и в следствиях к нему.

Пример 2.10 Имеются две концентрические окружности радиуса r и R. Слу-

чайная точка оказалась внутри большого круга. Какова вероятность того, что она в заштрихованном кольце?

Решение.

Вычислим площади кольца и круга и применим формулу (2.1)

SA = Sкольца = πR2 − πr2 = π(R2 − r2),

SΩ = Sкруга = πR2,

P (A) = SA/SΩ = π(R2 − r2)/(πR2) = 1 − r2/R2.

Пример 2.11 Какова вероятность того, что сумма двух наугад взятых положительных чисел, каждое из которых не больше единицы не превосходит 1, а их произведение будет не больше 2/9?

Решение. Пусть x, y - взятые числа. Имеем 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, то есть мно-

жество элементарных исходов имеет вид Ω = [0, 1] × [0, 1] и SΩ = Sквадрата = 1. Благоприятствующие интересующему нас событию A значения удовлетворяют

условиям: x + y ≤ 1, xy ≤ 2/9. Следовательно,

3Произвольное пространство элементарных исходов.

3.1 Общее определение вероятности. Аксиомы теории вероятностей.

До сих пор мы рассматривали такие случайные эксперименты, в которых количество исходов было конечным или счетным. Пусть Ω - произвольное множество.

Оно может быть как счетным, так и несчетным. Предположим, что для какогонибудь случайного эксперимента Ω является пространством всех элементарных событий, то есть все точки множества Ω являются исходами этого эксперимента, при этом в результате эксперимента появляется только одна точка из Ω.

Рассмотрим некоторую систему подмножеств Ω и обозначим ее S.

13

Определение 3.1 Совокупность множеств S называется алгеброй, если выпол-

нены следующие условия:

1.Ω S.

2.Если A S и B S, то A + B S.

3.Если A S, то A S.

Если Ω конечно, то в качестве алгебры S рассматривают систему всех подмножеств Ω.

Пример 3.1 Пусть Ω = {ω1, ω2}, тогда

S = {, [ω1], [ω2], [ω1; ω2]}.

Пусть Ω = {ω1, ω2, ω3}, тогда

S= {, [ω1], [ω2], [ω3], [ω1, ω2], [ω1, ω3], [ω2, ω3], [ω1; ω2; ω3]}.

Вобщем случае: если Ω содержит n элементов - card(Ω) = n, то S - алгебра всех подмножеств Ω содержит 2n элементов (ср. со св. 1 на стр. 8).

Пример 3.2 Пусть Ω = [0, 1), тогда на отрезке [0, 1) все множества, состоящие из конечного числа непересекающихся интервалов вида [a, b), a, b [0, 1) образуют

алгебру.

Используя свойства операций над событиями (подразд. 2.1) и определение алгебры S, нетрудно доказать следующие утверждения:

1. S, так как = Ω S.

2. Если A S, B S, то AB S, так как AB = A + B, откуда AB S и AB S.

пределы алгебры S. Это свойство называется замкнутостью относительно конеч-

ного числа действий над событиями. Если мы хотим чтобы вероятность обладала свойством непрерывности, то необходимо свойство замкнутости распространить на счетное число действий.

Определение 3.2 Алгебра A называется σ-алгеброй, если она замкнута относи-

тельно объединения любого счетного набора своих подмножеств. То есть требование 2 в определении алгебры заменяется требованием 2′: если Ai A, i = 1, 2, ...,

то P∞ Ai A.

i=1

Замечание 3.1 Если пространство элементарных исходов Ω конечно - card(Ω) = n, то алгера всех подмножеств, порожденная исходами ωi, i = 1, ..., n является σ- алгеброй. Если Ω счетно, то обычно рассматривают σ-алгебру всех подмножеств, которая содержит алгебру, порожденную исходами ωi, i = 1, 2, ..., но не равна ей, так как содержит подмножества A, такие, что количество элементов в A и в A - счетно. Например, A - подмножество всех элементов, занумерованными

нечетными номерами.

14

Замечание 3.2 Наименьшая σ-алгеброй на прямой, содержащая все интервалы называется борелевской σ-алгеброй и обозначается B (здесь "наименьшая"означает, что все остальные σ-алгебры, содержащие интервалы, влючают в себя все множества из борелевской σ-алгебры B).

Сопоставим событиям σ-алгебры A вероятности, то есть дадим аксиоматическое

определение вероятностной меры.

Определение 3.3 Вероятностной мерой P (A) называется числовая функция, заданная на σ-алгебре A подмножеств Ω : A Ω, A A и удовлетворяющая сле-

дующим условиям (аксиомам):

1)P (A) ≥ 0, для любого A A.

2)P (Ω) = 1 – условие нормировки.

3)Если события A1, A2, ..., Ai A, i = 1, 2, ... попарно несовместны, то есть AiAj = для любых i 6= j, то P (A) обладает свойством счетной аддитивности

Определение 3.4 Пара (Ω, A) называется измеримым пространством, множества A A называются измеримыми множествами или событиями, другие мно-

жества не рассматриваются.

Замечание 3.3 Совокупность всех множеств из Ω является алгеброй и σ- алгеброй, но если множество Ω не счетно, то нетривиальная вероятностная мера P (A), удовлетворяющая аксиомам определения 3.3, определенная на всех множествах из Ω может не сущесвовать. В рассмотренном выше примере 3.2 нельзя задать вероятностную меру на всех подмножествах Ω = [0, 1) (см., например, [11, cтр. 87, 93]). Поэтому обычно рассматривают B[0, 1) - борелевскую алгебру на отрезке [0, 1), которая содержит все возможные пересечения множеств из борелевской алгебры B на прямой и отрезка [0, 1).

Замечание 3.4 Вероятностная мера обладает свойством непрерывности: пусть последовательность событий {An A} такова, что An+1 An (убывающая по-

∞

T

следовательность множеств) и An = A, тогда P (An) → P (A) при n → ∞

n=1

(первая аксиома непрерывности) или An+1 An (возрастающая последователь-

∞

S

ность множеств) и An = A, тогда P (An) → P (A) при n → ∞ (вторая аксиома

n=1

непрерывности).

Более того, можно показать, что аксиомы непрерывности эквивалентны, а аксиома счетной аддитивности эквивалентна конечной аддитивности + любая

аксиома непрерывности.

Замечание 3.5 Если Ω R1, где R1 - вещественная прямая, то достаточно определить P (A) на интервалах, на остальные множества борелевской σ-алгебры

она продолжится по непрерывности (подробнее см. [11, ч. II, гл. 1, §1, 2] или [1, гл. 2, §1]).

15

Определение 3.5 Пусть Ω-пространство элементарных исходов, A - σ-алгебра подмножеств Ω, P - вероятностная мера заданная на σ-алгебре A. Тройка (Ω, A, P ) называется вероятностным пространством или вероятностной моде-

лью.

Условия в определении σ-алгебры A и условия 1, 2, 3 в определении вероятностной

меры составляют аксиомы теории вероятностей.

Свойства вероятностной меры. В подразд. 2.2 мы вывели свойства вероятностей, для случая конечного или счетного числа исходов эксперимента (такой эксперимент называется дискретным). В общем случае для вероятносной меры также справедливо утверждение 2.1, кроме того она обладает свойством счетной аддитивности и непрерывности.

В качестве примера приведем доказательство формулы сложения вероятностей для любых событий A и B в общем случае.

Пусть A и B - любые события. Тогда верна следующая формула

P (A + B) = P (A) + P (B) − P (AB)

Доказательство. Справедливы следующие представления:

A + B = A + (B − AB), B = AB + (B − AB)

В этих представлениях событие A и (B −AB), а также AB и (B −AB) несовместны.

Действительно

в первое из равенств получим формулу сложения вероятностей.

Заметим, что при доказательстве формулы сложения вероятностей мы вывели формулу (3.1), которая представляет самостоятельный интрес.

3.2 Условные вероятности. Умножение вероятностей. Независимость событий.

Рассмотрим классическую схему, в рамках которой все исходы равновозможны. Пусть Ω - пространство элементарных исходов. Предположим, что некоторое событие B, P (B) 6= 0 произошло. Будем рассматривать только те элементарные исходы, которые составляют событие B. Тогда Ω1 = B, новое пространство элементарных исходов. Выберем исходы из A, которые входят в B и обозначим их A1. Тогда

16

A1 = AB. В рамках классической схемы вероятность события A при условии, что событие B произошло есть число P (A|B):

P (A|B) = m(A1) = m(A1)/card(Ω) = P (AB) ,

card(Ω1) card(Ω1)/card(Ω) P (B)

так как card(Ω1) = m(B).

Дадим общее определение условной вероятности P (A|B), P (B) 6= 0.

Определение 3.6 Рассмотрим событие B, такое что P (B) 6= 0. Тогда условной вероятностью события A при условии, что событие B произошло, называется число, которое обозначается P (A|B) и вычисляется по формуле:

P (A|B) = P (AB) .

P (B)

Поскольку условная вероятность - это обычная вероятность, но лишь на более узком пространстве элементарных исходов, то для нее справедливы все свойства обычной вероятностной меры.

Свойства условных вероятностей.

Пусть P (B) 6= 0, тогда

1)P (Ω |B) = 1.

2)P ( |B) = 0.

3)0 ≤ P (A |B) ≤ 1.

4)Если A C, то P (A |B) ≤ P (C |B).

5)P (A|B) = 1 − P (A|B).

6)Формула сложения условных вероятностей. Для любых событий A и C

P((A + C)|B) = P (A|B) + P (C|B) − P (AC|B).

7)Формула умножения вероятностей.

Для любых событий A и B, P (B) 6= 0

P (AB) = P (B)P (A|B).

Эта формула является просто другой формой записи определения условной вероятности.

8) Общая формула умножения вероятностей.

Для любых событий A1, A2, ..., An, P (Ai) 6= 0, i = 1, ..., n − 1

P (A1 A2...An) = P (A1)P (A2|A1)P (A3|A1A2)...P (An|A1A2...An−1).

Независимость событий.

Определение 3.7 Событие A называется независимым от события B, если P (A|B) = P (A), то есть вероятность наступления события A не зависит от того, произошло событие B или нет.

17

Удобнее использовать определение взаимной независимости событий A и B.

Определение 3.8 События A и B называются независимыми, если P (AB) =

P (A) P (B).

При P (B) 6= 0 эти определения равносильны в силу формулы умножения вероятностей P (AB) = P (A|B)P (B) = P (A)P (B), но определение 3.8 не теряет смысла и при P (B) = 0. Заметим, что при P (A) 6= 0, P (B) 6= 0 из условия A не зависит от B следует, что B не зависит от A.

Свойства независимых событий.

1. Пусть A и B - независимые события, тогда события A и B также независимы. Доказательство. P (A B) = P ((Ω − A)B) = P (B − AB) = P (B) − P (AB) =

P (B) − P (A)P (B) = P (B)(1 − P (A)) = P (B)P (A).

При доказательстве использовали формулу (3.1) для нахождения вероятности

P (B − AB).

Следствие 3.1 Из независимости событий A и B следует в силу симметрии независимость B и A и независимость A и B.

2. Пусть события A и C, а также события B и C попарно независимы. Если события A и B несовместны, то события A + B и C независимы.

Доказательство. События AC и BC несовместны, следовательно, P ((A+B)C) =

P (AC + BC) = P (AC) + P (BC) = P (A)P (C) + P (B)P (C) = (P (A) + P (B))P (C) =

P (A + B)P (C).

Последнее равенство справедливо в силу аддитивности вероятностной меры.

Можно распространить определение независимости на совокупность событий.

Определение 3.9 События A1, A2, ..., An называются независимыми в совокупности, если для любого набора индексов 1 ≤ l1 ≤ l2 ≤ ... ≤ lk ≤ n выполняется

равенство:

P (Al1 · Al2 · ... · Alk ) = P (Al1 )P (Al2 )...P (Alk ).

Замечание 3.6 Из попарной независимости незавимость в совокупности не следует (см. [11, стр. 25], [1, гл. 2, §3, пр. Бернштейна] или см. [13], [3]). Независимыми в совокупности являются, например, испытания в схеме Берлулли, изучаемой в подразд. 3.3 - 3.4.

Также вводят понятие независимости испытаний или экспериментов. Для независимых испытаний P (A1A2) = P (A1)P (A2), если A1, и A2 любые события

происходящие в результате разных испытаний (подробнее см. [1, гл. 2, §3]). В частности, в примере 2.6 можно было вместо того, чтобы задавать вероятность P (AB), добавить условие независимости испытаний - стрелки стреляют

независимо друг от друга.

18

Пример 3.3 Урна содержит 20 шаров, из которых 8 шаров черного цвета, 12 - белого. Найти вероятность того, что при последовательном извлечении трех каких - либо шаров все они окажутся белыми (извлеченные шары в урну не возвращаются. )

Пусть A - первый шар белый, B - второй шар белый, C - третий шар белый.

Тогда

P (ABC) = P (A)P (B/A)P (C/AB) = 1220 · 1119 · 1018 = 1157 .

Пример 3.4 33 буквы русского алфавита написаны на карточках разрезной азбуки. Шесть карточек выбираются наугад, одна за другой и укладываются на стол в порядке появления. Найти вероятность того, что получено слово "теория ".

P (A) = 331 · 321 · 311 · 301 · 291 · 281 = 27!33! .

Заметим, что в двух последних примерах можно считать, что предметы извлекаются не последовательно один за другим, а одновременно три шара или шесть карточек. Такая постановка задачи эквивалентна приведенной выше и приводит к классической схеме. Например в примере 3.4 в качестве элементарных исходов можно рассмотреть множество упорядоченных наборов по шесть карточек, случайно выбранных из 33 данных. Тогда количество элементарных исходов card(Ω) = A633 и эти исходы можно считать равновозможными. Событию A - в результате получено слово "теория", благоприятен один исход. Следовательно, P (A) = 1/A633 = 27!/33!.

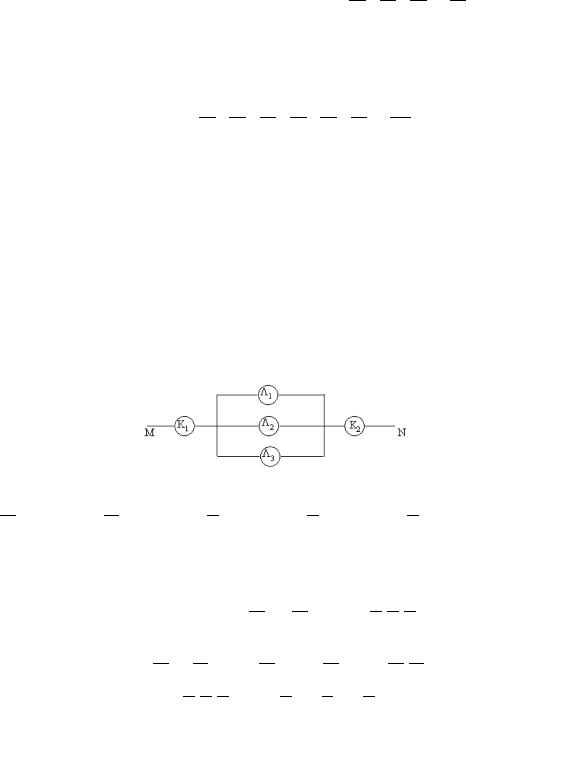
Пример 3.5 ( независимые события ) Электронная цепь между точками M и N составлена по схеме:

Выход из строя за время T различных элементов цепи - независимые события

P (K1) = 0, 6; P (K2) = 0, 5; P (Λ1) = 0, 4; P (Λ2) = 0, 7; P (Λ3) = 0, 9. Здесь черта

означает выход из строя соответствующего элемента цепи. Определить вероятность разрыва цепи за время T .

Решение. Пусть событие C - разрыв цепи за время T , событие A - выход из строя элементов K1 или K2, событие B - одновременный выход из строя элементов

Λ1, Λ2, Λ3. Тогда C = A + B, A = K1 + K2, B = Λ1Λ2Λ3. Отсюда, используя

независимость событий и формулу сложения вероятностей, имеем

P (A) = P (K1 + K2) = P (K1) + P (K2) − P (K1K2) = 0, 8

P (B) = P (Λ1Λ2Λ3) = P (Λ1)P (Λ2)P (Λ3) = 0, 252.

P (A + B) = P (A) + P (B) − P (AB) = 0, 8 + 0, 252 − 0, 8 · 0, 252 = 0, 8504.

19

3.3Формула полной вероятности и формула Байеса

Пусть требуется определить вероятность некоторого события A, которое может произойти вместе с одним из событий H1, H2, ..., Hn.

Определение 3.10 Набор H1, H2, ..., Hn называется полной группой событий, если они попарно несовместны, то есть HiHj = для любых i 6= j, и их сумма

является достоверным событием, то есть Pn Hi = Ω. В этом случае, события

i=1

H1, H2, ..., Hn называются гипотезами.

В дальнейшем без потери общности (так как P (AHi) = 0 при P (Hi) = 0) будем предполагать, что P (Hi) 6= 0, i = 1, ..., n.

Теорема 3.1 (формула полной вероятности) Пусть H1, H2, ..., Hn - полная группа событий. Тогда для любого события A

n

X

P (A) = P (Hi)P (A|Hi)

i=1

Доказательство. A = AΩ = A(H1 + H2 + ... + Hn) = AH1 + AH2 + ... + AHn. Так как

Hi попарно несовместны, то и события AHi также попарно несовместны. Имеем (AHi)(AHj ) = A(Hi · Hj ) = для любых i 6= j. Тогда

P (A) = P (AH1 + AH2 + ... + AHn) = P (AH1) + P (AH2) + . . . +

+ P (AHn) = P (H1)P (A|H1) + P (H2)P (A|H2) + ... + P (Hn)P (A|Hn)

последнее утверждение следует из формулы "умножения вероятностей"(свойства 7

условных вероятностей). Теорема доказана

Пример 3.6 Имеются две урны: в первой a белых шаров и b черных; во второй c белых и d черных. Из первой урны во вторую перекладывают, не глядя, один

шар. После этого из второй урны берут один шар. Найти вероятность того, что этот шар будет белым.

Решение. Пусть событие A - появления белого шара из второй урны. Рассмотрим

следующие гипотезы:

H1 - во вторую урну переложен белый шар,

H2 - во вторую урну переложен черный шар.

В силу того, что шары перекладывались случайно, возникает классическая схема.

го находится a + b шаров, из них a белых и b черных. После перекладывания во второй урне c + d + 1 шар и либо c + 1, либо c белых шаров.

20

Следствием формулы полной вероятности является формула Байеса. А именно, справедлива теорема:

Теорема 3.2 (формула Байеса) Пусть заданы H1, H2, ..., Hn - полная группа событий и событие A, P (A) 6= 0. Тогда для любого i = 1, 2, ..., n условная вероятность события Hi при условии, что событие A произошло, задается формулой:

Доказательство. В силу определения условной вероятности имеем P (Hi|A) = P (HiA)|P (A). Используя формулу умножения вероятностей и формулу полной вероятности для нахождения P (A) получаем формулу Байеса.

Пример 3.7 В группе из 10 студентов, пришедших на экзамен, 3 подготовленных отлично, 4 - хорошо, 2 - удовлетворительно и 1 - неудовлетворительно. В экзаменационных билетах 20 вопросов. Отлично подготовленный студент может ответить на все вопросы, хорошо подготовленный на 16, удовлетворительно - на 10, неудовлетворительно - на 5. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что этот студент подготовлен:

а) отлично, б) неудовлетворительно.

Решение. Пусть A событие, состоящее в том, что студент ответил на 3 во-

проса. Рассмотрим четыре гипотезы: H1 - студент подготовлен отлично; H2 - хорошо;

H3 - удовлетворительно;

H4 - неудовлетворительно.

До опыта вероятности гипотез были P (H1) = 0, 3; P (H2) = 0, 4; P (H3) =

0, 2; P (H4) = 0, 1. Найдем условные вероятности P (A|Hi), i = 1, 2, 3, 4. Имеем для отлично подготовленного студента P (A/H1) = 1.

Для хорошо подготовленного студента вероятность ответить на первый вопрос 16/20, при ответе на 2-ой вопрос студент знает 15 вопросов из 19, на 3-й - 14 из 18, откуда

P (A|H2) = (16/20)(15/19)(14/18) 0, 4912.

Аналогично

21

По формуле полной вероятности: P (A) 0, 5184. По формуле Байеса находим условные вероятности гипотез H1 и H4:

Заметим, что в соответствии с естественным представлением при условии правильного ответа на три вопроса, вероятность гипотезы H1 - студент подготовлен отлично увеличилась, а гипотезы H4 - студент подготовлен неудовлетво-

ритльно уменьшилась.

3.4Последовательные испытания. Схема и формула Бернулли.

Схема Бернулли заключается в следующем. Производится n последовательных независимых испытаний с двумя исходами - A и A . Вероятность появления события A в каждом испытании одна и та же P (A) = p. Нас будет интересовать вероятность того, что в серии из n таких испытаний, событие A произойдет ровно m раз. Обозначим буквой q вероятность дополнительного к A события A, то есть

P (A) = q, где q = 1 − p.

Теорема 3.3 (формула Бернулли) . Справедлива формула:

где Pn(m) - вероятность того, что при n испытаниях событие A произойдет ровно m раз.

Доказательство. Рассмотрим сначала частный случай n = 4, m = 2. Событие A в четырех испытаниях произошло 2 раза. Тогда возможны следующие случаи:

A A A A, A A A A, A A A A, A A A A, A A A A и A A A A. Может реализоваться любая из этих цепочек. Вероятность любой из этих цепочек одна и та же и равна p2q2. Таких цепочек C42 = 6 то есть P4(2) = C42p2q2.

выбрать для события A "m" мест из общего числа "n" мест есть число сочетаний

из "n" по "m", откуда

Pn(m) = Cnmpmqn−m.

Частные случаи формулы Бернулли. Будем называть появление события A

успехом, появление события A неудачей.

1.Вероятность одних успехов: Pn(n) = Cnmpnq0 = pn.

2.Вероятность одних неудач: Pn(0) = qn.

3.Вероятность хотя бы одного успеха: Pn(m ≥ 1) = 1 − qn.

4.Вероятность хотя бы одной неудачи: Pn(m < n) = 1 − pn.

22