It_Kompyuterny_Praktikum

Редактор нечетких систем в среде MATLAB также позволяет графически просматривать зависимость выходной переменной от ее входных

(рис. 4.16).

Выводы (пример):

В ходе выполнения данной лабораторной работы я изучил построение элементарных нечетких экспертных систем на выбранном мною практическом примере используя редактор Fuzzy среды MATLAB.

Контрольные вопросы

1.Что такое экспертная система?

2.Что такое знания и в чем их отличия от данных?

3.Что такое база знаний и в чем ее отличие от базы данных?

4.Сколько переменных в Вашей нечеткой системе и сколько функций принадлежности у каждой из них и почему?

5.Какие типы функций принадлежности Вы использовали при выполнении лабораторной работы?

6.Какие типы функций принадлежности использовались в лабораторной работе и почему?

7.Как задается набор правил?

8.В чем отличие нечеткого логического вывода типа Mamdani от логического вывода типа Sugeno?

9.Опишите этапы нечеткого вывода.

10.Опишите структуру экспертной системы.

11.Перечислите основные достоинства и недостатки систем с нечеткой логикой?

2.3. Программирование нечеткой системы в среде MATLAB с использованием встроенных функций

программирования нечетких систем с помощью встроенных функций пакета нечеткой логики программной среды MATLAB.

Задание: Необходимо запрограммировать нечеткую систему, необходимую для аппроксимации табличной функции yi f (xi ) , i 1.10 . Варианты задания представлены в табл. 4.1.

Пример выполнения:

Задача. В данной лабораторной работе необходимо запрограммировать нечеткую систему для аппроксимации таблично заданной функции. Для

51

примера возьмем таблично заданную функцию из примера к лабораторной работе 1 (табл. 4.2).

Пакет Fuzzy Logic Toolbox наделен множеством функций для создания нечетких систем (Приложение 1).

Для программирования нечеткой системы для аппроксимации таблично заданной функции из примера к лабораторной работе № 1 достаточно написать следующий программный код:

a=newfis('approxim','sugeno'); % создание нечеткой системы типа Сугено a=addvar(a,'input','x',[0 1]); % добавляем входную переменную х с диапазоном

изменений от 0 до 1 a=addvar(a,'output','y',[0 3]); % добавляем выходную переменную у с

диапазоном изменений от 0 до 3 a=rmmf(a,'input',1,'mf',1);%удаление функций принадлежности входной и

выходной переменных создаваемых по умолчанию при создании нечеткой системы (необходимо для версии MATLAB ниже версии 7.5)

a=rmmf(a,'input',1,'mf',2);

a=rmmf(a,'input',1,'mf',1);

a=rmmf(a,'output',1,'mf',1);

a=rmmf(a,'output',1,'mf',2);

a=rmmf(a,'output',1,'mf',1);

a=addmf(a,'input',1,'mf1','gaussmf',[0.05 0.1]); % добавляем функцию принадлежности mf1 гауссовского типа для входной переменной с диапазоном изменений от 0,05 до

0,1 a=addmf(a,'input',1,'mf2','gaussmf',[0.05 0.2]); a=addmf(a,'input',1,'mf3','gaussmf',[0.05 0.3]); a=addmf(a,'input',1,'mf4','gaussmf',[0.05 0.4]); a=addmf(a,'input',1,'mf5','gaussmf',[0.05 0.5]); a=addmf(a,'input',1,'mf6','gaussmf',[0.05 0.6]); a=addmf(a,'input',1,'mf7','gaussmf',[0.05 0.7]); a=addmf(a,'input',1,'mf8','gaussmf',[0.05 0.8]); a=addmf(a,'input',1,'mf9','gaussmf',[0.05 0.9]); a=addmf(a,'input',1,'mf10','gaussmf',[0.05 1]); a=addmf(a,'output',1,'mf1','constant',[2.05]); % добавляем функцию

принадлежности mf1 для выходной переменной, которая является константой равной 2,05

a=addmf(a,'output',1,'mf2','constant',[1.94]);

a=addmf(a,'output',1,'mf3','constant',[1.92]);

a=addmf(a,'output',1,'mf4','constant',[1.87]);

a=addmf(a,'output',1,'mf5','constant',[1.77]);

52

a=addmf(a,'output',1,'mf6','constant',[1.74]);

a=addmf(a,'output',1,'mf7','constant',[1.71]);

a=addmf(a,'output',1,'mf8','constant',[1.6]);

a=addmf(a,'output',1,'mf9','constant',[1.56]);

a=addmf(a,'output',1,'mf10','constant',[1.4]);

Поясним, как формируется база знаний. При программировании база знаний представляет собой матрицу, каждая строка которой представляет собой правило. Матрица правил состоит из m+n+2 столбцов, где m- количество входных переменных, n – количество выходных переменных. Первые m столбцов отражают входы системы. Каждый из этих столбцов отражают индекс функции принадлежности соответствующей входной переменной. Следующие n столбцов отражают выходы системы. Каждый из этих столбцов отражают индекс функции принадлежности соответствующей выходной переменной. m+n+1 столбец отражает вес правила в базе знаний. Вес представляет собой число от 0 до 1. m+n+2 столбец показывает связку между входными переменными в правиле. Если значение равно 1, то между входами ставится знак И (AND). Если значение равно 2, то между входами ставится знак ИЛИ (OR). Таким образом MATLAB интерпретирует, например, первую строку нашей базы знаний следующим образом:

If (x is mf1) then (y is mf1)

В результате работе нашей программы была построена следующая нечеткая системы (рис. 4.17–4.22):

53

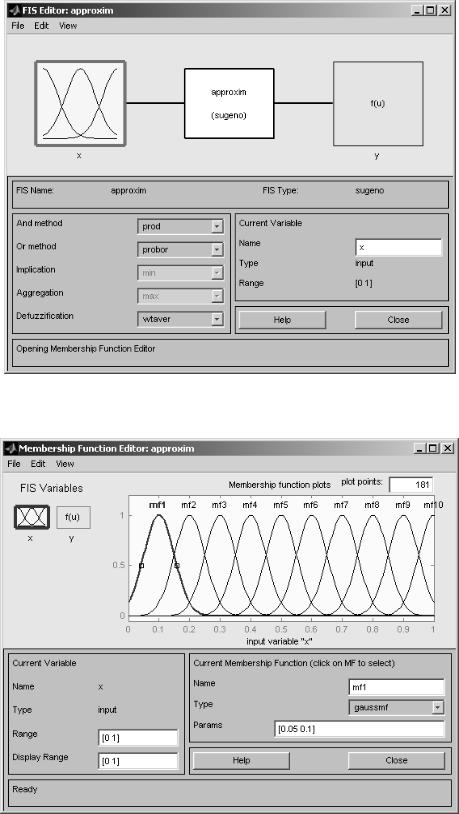
Рис. 4.17. Окно редактора функции

Рис. 4.18. Окно функций принадлежности входной переменной

54

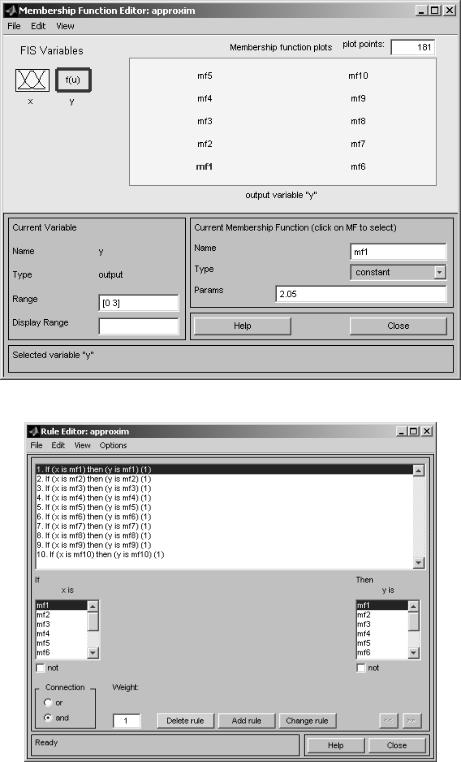
Рис.4.19. Окно функций принадлежности выходной переменной

Рис. 4.20. Окно редактора правил

55

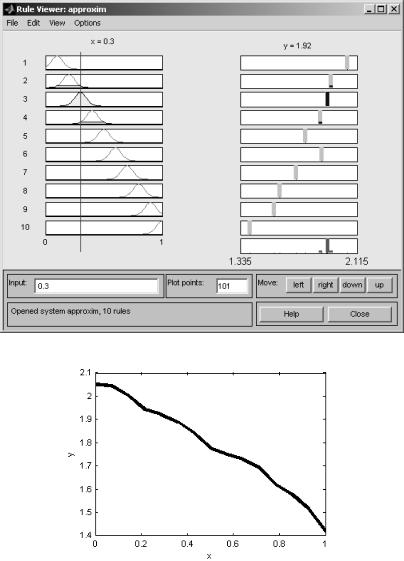
Рис.4.21. Окно просмотра правил

Рис. 4.22. График функции

Выводы (пример):

В результате выполнения лабораторной работы мною были освоены навыки программирования нечетких систем в математической среде MATLAB с использованием встроенных функций. С помощью этих функций мною была построена нечеткая система для аппроксимации таблично заданной функции.

Контрольные вопросы:

1.Какая команда используется для добавления переменной? Опишите параметры функции.

2.Каким образом задаются и добавляются правила в программном коде?

3.Опишите команду вывода функций принадлежности.

4.Каким образом задаются типы функций принадлежности?

56

2.4. Кластеризация с помощью алгоритма нечетких центров

Цель: Освоить методику нахождения центров кластеров.

Задание: Найти центры кластеров, используя алгоритм нечетких центров с помощью программы Clustering (Кластеризация), входящий в пакет Fuzzy Logic Toolbox математической среды MATLAB.

Основные теоретические сведения [45]:

Кластеризация – это объединение объектов в группы (кластеры) на основе схожести признаков для объектов одной группы и отличий между группами. Кластер (от английского cluster) – гроздь, пучок, скопление, группа элементов, характеризуемых каким-либо общим свойством.

Кластеризация помогает представить неоднородные данные в более наглядном виде и для дальнейшего, более удобного, использования этих данных.

Кластеризация может быть использована для решения следующих задач:

обработка изображений;

классификация;

тематический анализ коллекций документов;

построение репрезентативной выборки.

Кластерный анализ предназначен для разбиения множества объектов на заданное или неизвестное число классов на основании некоторого математического критерия качества классификации. Критерий качества кластеризации в той или иной мере отражает следующие неформальные требования:

внутри групп объекты должны быть тесно связаны между собой;

объекты разных групп должны быть далеки друг от друга.

Эти требования выражают стандартную концепцию компактности классов разбиения. Узловым моментом в кластерном анализе считается выбор меры близости объектов (метрики), от которого решающим образом зависит окончательный вариант разбиения объектов на группы при заданном алгоритме разбиения. В каждой конкретной задаче этот выбор производится по-своему, с учетом главных целей исследования, физической и статистической природы используемой информации и т.д.

В кластерном анализе так же важно расстояние между целыми группами объектов. Приведем примеры наиболее распространенных расстояний и мер близости, характеризующих взаимное расположение отдельных групп объектов.

Пусть:

i – i-я группа (класс, кластер) объектов;

57

Ni – число объектов, образующих группу i , каждый объект представляет собой точку в n-мерном пространстве;

i – среднее арифметическое объектов, входящих в i (т.е. i – «центр тяжести» i-й группы);

p – число групп (кластеров); x i – i-й объект кластера;

q ( l , m ) – расстояние между группами l и m .

1

2

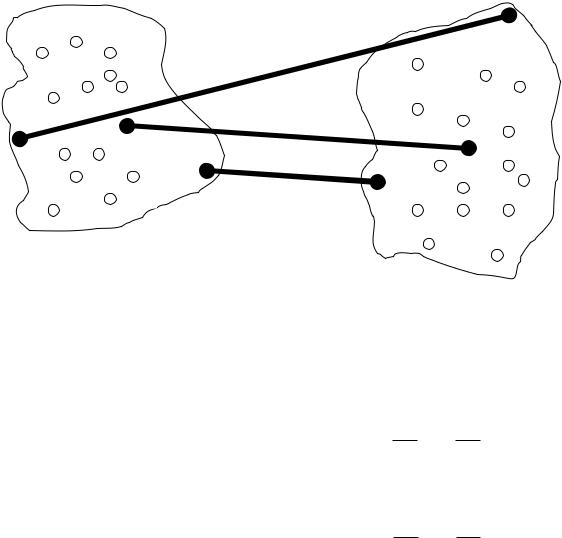
Рис. 4.23. Различные способы определения расстояния между кластерами l иm : 1 – по самым далеким объектам , 2 – по центрам тяжести, 3 – по ближайшим объектам

Расстояние ближайшего соседа есть расстояние между ближайшими объектами кластеров (рис. 4.23):

qmin ( l , m ) min d (xi , x j ),i 1, p, j 1, p .

Расстояние дальнего соседа – расстояние между самыми дальними объектами кластеров (рис. 5.23):

qmin ( l , m ) max d (xi , x j ),i 1, p, j 1, p .

Расстояние центров тяжести равно расстоянию между центральными точками кластеров (рис. 4.23):

q( l , m ) d( l , m ).

Выбор той или иной меры расстояния между кластерами влияет на вид выделяемых алгоритмами кластерного анализа геометрических группировок объектов в пространстве признаков. Так, алгоритмы, основанные на

58

расстоянии ближайшего соседа, хорошо работают в случае группировок, имеющих сложную, в частности, цепочечную структуру. Расстояние дальнего соседа применяется, когда искомые группировки образуют в пространстве признаков шаровидные облака. И промежуточное место занимают алгоритмы, использующие расстояния центров тяжести и средней связи, которые лучше всего работают в случае группировок эллипсоидной формы.

Алгоритмы кластерного анализа отличаются большим разнообразием. Это могут быть, например, алгоритмы, реализующие полный перебор сочетаний объектов или осуществляющие случайные разбиения множества объектов. В то же время большинство таких алгоритмов состоит из двух

этапов:

на втором этапе объекты переносятся из класса в класс до тех пор, пока значение критерия не перестанет улучшаться.

Таким образом, алгоритмы кластеризации основаны на подобии образов и размещают близкие образы в один кластер.

Выявление центров – это значимый этап при предварительной обработке данных, так как он позволяет сопоставить с этими центрами функции принадлежности переменных при проектировании системы нечеткого вывода.

Программа Clustering (Кластеризация) пакета Fuzzy Logic Toolbox математической среды MATLAB выявляет центры кластеров, т.е. точки в многомерном пространстве данных, около которых группируются (скапливаются) экспериментальные данные.

В программе Clustering (Кластеризация) используются два алгоритма выявления центров кластеров: Subtractive clustering (вычитающая кластеризация) и Fuzzy c-means (алгоритм нечетких центров).

В основе первого алгоритма лежит предложение, что каждая экспериментальная точка может быть центром кластера, при этом вначале для каждой точки вычисляется мера правдоподобия данного предположения («потенциал точки»), основанная на плотности точек в заданной окрестности рассматриваемой. Дальнейшие вычисления происходят итеративно:

1)точка с наибольшим потенциалом объявляется центром первого кластера;

2)из отмеченной окрестности этой точки удаляются все остальные точки;

3)из оставшихся точек объявляется центр следующего кластера и т.д., пока не будут рассмотрены (исключены или объявлены центрами) все точки.

59

Алгоритм Fuzzy c-means является более точным, для его работы требуется задание таких опций, как число кластеров и число итераций. Рассмотрим его более подробно.

Кластеризация на основе алгоритма нечетких центров. На основе нечеткого c-means алгоритма выполняется кластеризация данных. Этот алгоритм кластеризации предложил Джеймс Бэздэк (James Bezdek) в 1981 году.

Существует множество методов кластеризации, которые можно классифицировать на четкие и нечеткие. Четкие методы кластеризации разбивают исходное множество объектов X на несколько непересекающихся подмножеств. При этом любой объект из X принадлежит только одному кластеру. Нечеткие методы кластеризации позволяют одному и тому же объекту принадлежать одновременно нескольким (или даже всем) кластерам, но с различной степенью истинности. Нечеткая кластеризация во многих ситуациях более «естественна», чем четкая, например, для объектов, расположенных на границе кластеров.

Задача нечеткой кластеризации ставится следующим образом:

Дано:

X (x1T , xT2 ,...xTn )T – объекты, подлежащие кластеризации, где n –

Необходимо каждому элементу множества X поставить в соответствие степени принадлежности к классам.

Элементы одного кластера должны быть так близки друг к другу, как это только возможно, и, одновременно, кластеры должны быть на наибольшем удалении друг от друга. Для обеспечения управляемости процесса кластеризации необходимо использовать меру близости, в качестве которой обычно определяют расстояние между двумя объектами (точками в p-мерном пространстве) xk и xl в виде вещественной функции

d : x x R такой что:

d (xk , xl ) dkl 0;

dkl 0 xk xl ;

dkl dlk .

Дополнительно, если функция d удовлетворяет правилу треугольника, т.е. dkl dkj d jl , тогда эта функция является метрикой, хотя выполнение

этого свойства не всегда необходимо для задач кластеризации.

60