
матрица переходных вероятностей
.docxМатрицы вероятностей перехода являются средством описания поведения марковской цепи. Каждый элемент этой матрицы представляет собой вероятность перехода из заданного состояния (которому соответствует строка) к следущему состоянию (которому соответствует столбец). В этой матрице предусмотрены все возможные переходы данного множества состояний. Условно такую матрицу записывают в общем виде следующим образом:
|
|
|
s1 |
s2 |
s3 |
|
|
s1 |
p11 |
p12 |
p13 |
|
P = |
s2 |
p21 |
p22 |
p23 |
|
|
s3 |
p3 |
p32 |
p33 |
|
|
|
|
|
|
где P - матрица переходных вероятностей, pi,j - вероятность перехода из состоянийs1,s2.,s3, соответствующих строкам матрицы, в состояния s1,s2.,s3, соответствующие столбцам. Отметим еще раз, что в данном случае имеется в виду цепь первого порядка, т.е. такая форма марковского процесса, для которой каждое конкретное состояние зависит только от непосредственно предшествующего. Процессы, которые можно описывать и моделировать с помощью матриц переходных вероятностей, должны обладать марковским свойством, или просто марковостью - под этим понимают наличие зависимости вероятности конкретного состояния от непосредственно предшествующего (или предшествующих, для цепей высоких порядков). Положим в ящик три красных шара, два синих и один зеленый, и будем наудачу доставать их, отмечать цвет и класть обратно. Понятно, что вероятность выбрать красный шар всегда будет равна 1/2, синий - 1/3 и зеленый - 1/6. При этом не важно, какого цвета шар был выбран только что. Следовательно, матрица вероятностей перехода будет состоять из трех одинаковых строк (лист "Examples", пример 1) и данный процесс не обладает марковским свойством. Для проверки наличия марковского свойства используют статистический подход и критерий 2.
Матрицы вероятностей перехода типа приведенной в таблице 4.2.2. описывают одношаговый процесс - переход от одного состояния к другому, непосредственно следующему за ним. Иногда представляет интерес исследование перехода более, чем в один шаг. Значения вероятностей переходов в n шагов можно определить путем возведения в степень n матрицы переходов. Пусть исходная матрица имеет вид
|
|
|
|
s1 |
s2 |
s3 |
|
|
|
s1 |
0 |
1 |
0 |
|
P |
= |
s2 |
0 |
1/3 |
2/3 |
|
|
|
s3 |
1/2 |
0 |
1/2 |
а исходное состояние =1. Проанализируем возможные варианты состояний, которые могут наступить через три шага. Состояние 1 может смениться только состоянием 2. Состояние 2 может сохраниться или смениться на 3. Возможные переходы показаны на рис. 4.3.1.
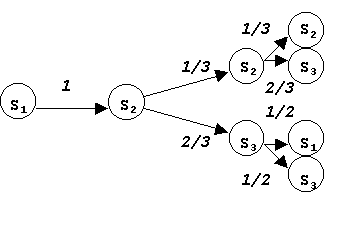
Рисунок 4.3.1.
Таким образом, состояния 3 можно достичь двумя путями. По правилам теории вероятностей "последовательные" шаги следует перемножать, а "параллельные" складывать; вероятность достичь состояния 3 через три шага при исходном состоянии 1:
(3) P13 = (1)(1/3)(2/3) + (1)(2/3)(1/2) = 5/9
Как и в случае матрицы, соответствующей одному шагу, сумма по строкам равна 1.
