Тема 7. Функция распределения и плотность распределения вероятностей непрерывной случайной величины

Непрерывная случайная величина может быть задана функцией распределения (называемой также интегральной функцией распределения)

или же плотностью распределения вероятностей (называемой также дифференциальной функцией распределения):

(1)

Равенство (1) имеет место в точках непрерывности функции .

Зная плотность распределения вероятностей, можно найти функцию распределения:

(2).

Свойства плотности распределения вероятностей:

1.

2. . (3)

В частности, если все возможные значения случайной величины принадлежат интервалу (a,b), то

.

Вероятность того, что непрерывная случайная величина примет значение, определяется равенствами:

. (4).

Задача образец.

Случайная величина задана плотностью распределения вероятностей:

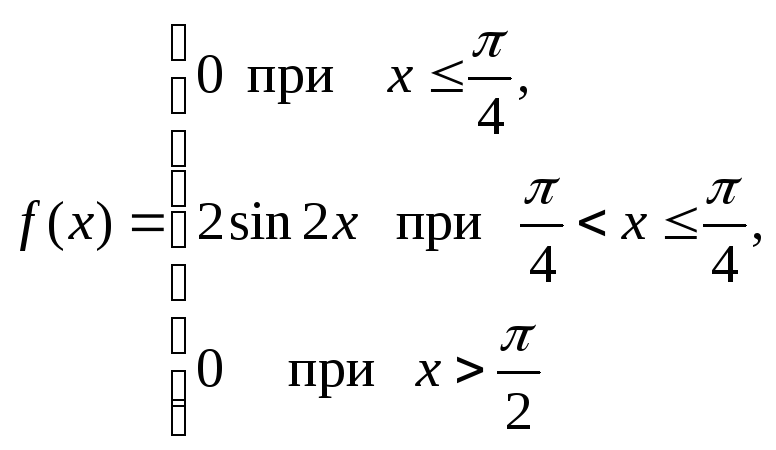
Найти функцию распределения

Решение. Если , то, следовательно,

Если , то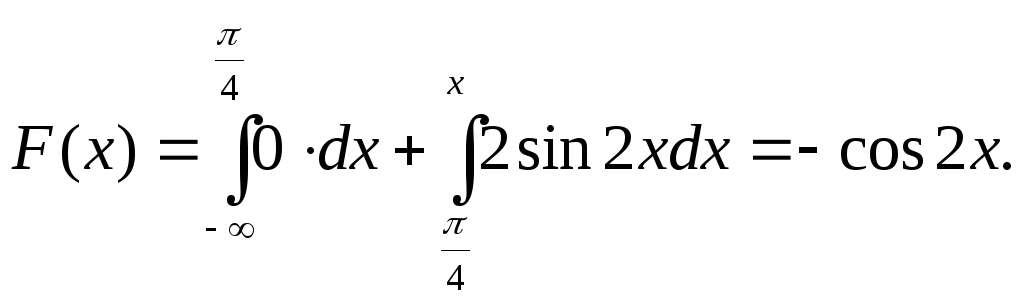

Если , то

Таким образом, случайная величина имеет следующую функцию распределения:

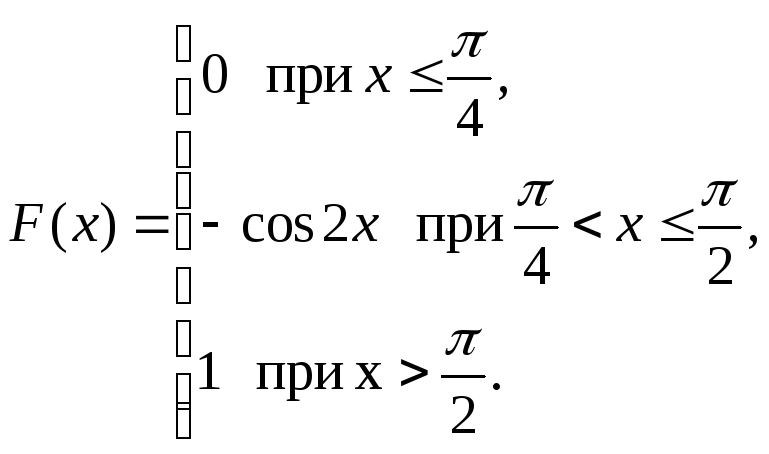
Задача 1.

Случайная величина задана функцией распределения

Найти:

а) плотность распределения вероятностей ;

б) графики функций и;

в) по известной функции и по найденной функциинайти вероятность того, что в результате испытанияпримет значения, не меньшее 2,1 и не большее 2,5.

Дать геометрическую интерпретацию величины найденной вероятности

Ответ: а) ;

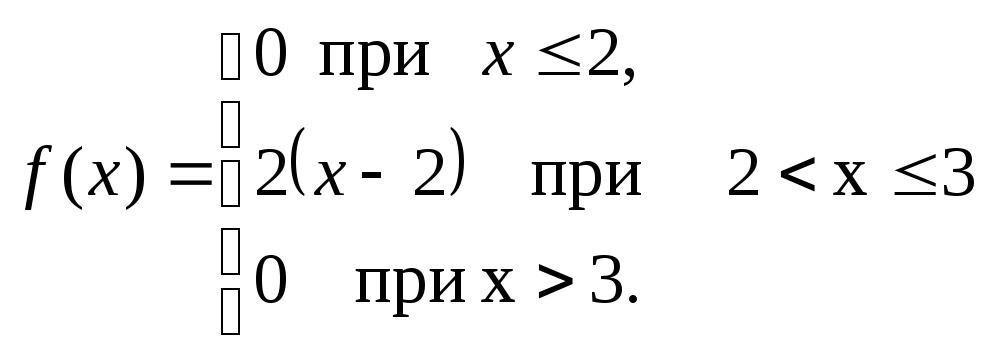б)

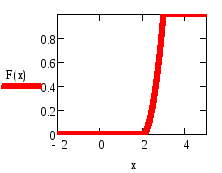
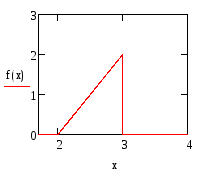
в) 0,24.

Задача 2.

Случайная величина задана функцией распределения

Найти:

а) постоянные bи с.

б) плотность распределения вероятностей величины .

Ответ: а) ;

б)

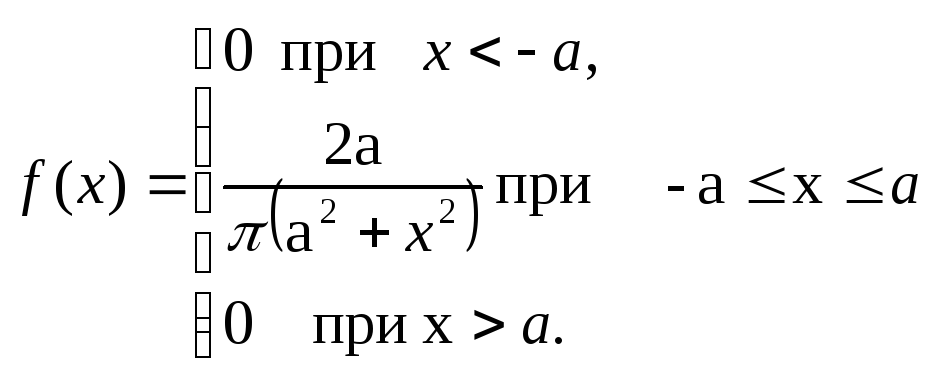
Задача 3.

Случайная величина , все возможные значения которой принадлежат интервалу, задана в этом интервале плотностью распределения вероятностей. Найти коэффициент.

Ответ:

Задача 4.

График плотности распределения вероятностей случайной величиныимеет вид, изображенной на рис. 1.

Найти аналитическое выражение для на всей числовой оси.

Ответ:

Задача 5.

Случайная величина подчинена закону Симпсона (закону равнобедренного треугольника) на отрезкерис.2.

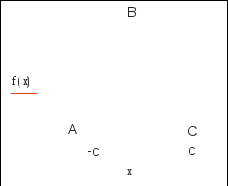
Указание:

Уравнения прямой и прямойнайти из уравнения, гдеотрезки отсекаемые прямой на осях. Получиться дляи для.

Найти:

а) плотность распределения вероятностей этой случайной величины;

б) вероятность попадания величины в интервал

ответ: а)

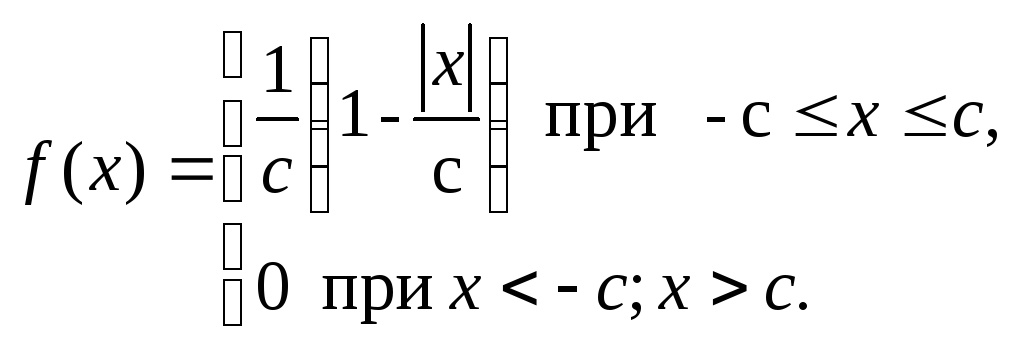
Задача 6.

Дана функция . Найти значение постоянного множителя, при котором эта функция могла бы характеризовать плотность распределения вероятностей случайной величиныпри условии, что все возможные значения величинынаходятся на луче.

Ответ: .

Задача 7.

Дана функция . Найти такое значение постоянного множителя, при котором эта функция могла бы охарактеризовать плотность распределения вероятностей случайной величиныпри условии, что.

Ответ: .

Задача 8.

Случайная величина на всей числовой оси задана дифференциальной функцией распределения(закон Коши).

Найти:

а) функцию распределения случайной величины ;

б) вероятность того, что в результате испытания примет значение из интервала.

Ответ: а); б).