17. Обобщенные силы системы с n степенями свободы.

Каждой обобщенной координате можно вычислить соответствующую ей обобщенную силу Q_k.

Вычисление производится по такому правилу.

Чтобы определить обобщенную силу Q_k, соответствующую обобщенной координате q_k, надо дать этой координате приращение (увеличить координату на эту величину), оставив все другие координаты неизменными, вычислить сумму работ всех сил, приложенных к системе, на соответствующих перемещениях точек и поделить ее на приращение координаты :

(7)

где – перемещение i-той точки системы, полученное за счет изменения k–той обобщенной координаты.

Обобщенная сила определяется с помощью элементарных работ. Поэтому эту силу можно вычислить иначе:

И так как есть приращение радиуса-вектора за счет приращения координаты при остальных неизменных координатах и времени t, отношение можно определять как частную производную . Тогда

(8)

где координаты точек – функции обобщенных координат (5).

Если система консервативная, то есть движение происходит под действием сил потенциального поля, проекции которых , где , а координаты точек – функции обобщенных координат, то

(9)

Обобщенная сила консервативной системы есть частная производная от потенциальной энергии по соответствующей обобщенной координате со знаком минус.

Конечно, при вычислении этой обобщенной силы потенциальную энергию следует определять как функцию обобщенных координат

П = П(q₁, q₂, q₃,…,q_s).

Замечания.

Первое. При вычислении обобщенных сил реакции идеальных связей не учитываются.

Второе. Размерность обобщенной силы зависит от размерности обобщенной координаты. Так если размерность [q] – метр, то размерность

= Нм/м = Ньютон, если [q] – радиан, то = Нм; если [q] = м², то и т.п.

Пример 23. По качающемуся в вертикальной плоскости стержню скользит колечко М весом Р (рис.72). Стержень считаем невесомым. Определим обобщенные силы.

Рис.72

Система имеет две степени свободы. Назначаем две обобщенные координаты s и .

Найдем обобщенную силу, соответствующую координате s. Даем приращение этой координате, оставляя координату неизменной, и вычислив работу единственной активной силы Р, получим обобщенную силу

.

Затем даем приращение координате , полагая s = const. При повороте стержня на угол точка приложения силы Р, колечко М, переместится на . Обобщенная сила получится

.

Так как система консервативная, обобщенные силы можно найти и с помощью потенциальной энергии . Получим и Получается гораздо проще.

18. Уравнение Лагранжа для одно-степенной механической системы

Теорема Лагранжа. Движение одностепенной голономной стационарной механической системы в ИСО (или ПСО с дополнительными силами) подчинено дифференциальному уравнению Лагранжа, которое составляется по формуле:

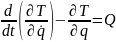
(1)

при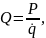

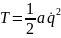
Таким образом, полная производная по времени от так называемого обобщенного импульса 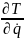, за вычетом частной производной вида 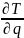, равна обобщенной силе Q.

Замечание 1. Действующие силы можно подразделять на потенциальные и непотенциальные, и применять уравнение Лагранжа в форме:

Здесь П(q) — потенциальная энергия системы потенциальных сил,

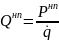— обобщенная сила системы непотенциальных сил.

Иногда уравнения Лагранжа записывают в форме Q-LT=0 ,

где 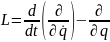— называется оператором Лагранжа и представляет собой совокупность математических действий над функцией T. Функцию S=-LT можно назвать обобщенной силой инерции системы. В таком случае можно сказать, что при движении механической системы, обобщенная сила системы приложенных сил уравновешивается обобщенной силой системы инерционных сил , Q + S = 0.

Замечание 2. Уравнению Лагранжа для стационарных голономных

одностепенных систем можно придать вид:

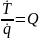
(2)

при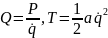

т.е. полная производная по времени от кинетической энергии одностепенной стационарной системы, отнесенная к обобщенной скорости равна обобщенной силе.

В результате выполнения математических действий в уравнении (1) или (2) получаем следующий более конкретный вид динамического уравнения.

Теорема. Математической моделью движения одностепенной

голономной стационарной системы служит дифференциальное уравнение

второго порядка:

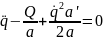при

Или

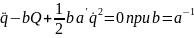
к которому присоединяют начальные условия, начальную фазу движения механической системы, задаваемое отдельно в виде двух конкретных

начальных значений фазовых переменных:

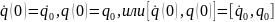
Т

(3)

еорема. Движение одностепенной голономной стационарной механической системы в случае постоянного коэффициента инерции a=const подчинено дифференциальному уравнению второго порядка вида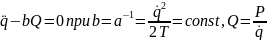

Уравнение (3) имеет простой смысл: обобщенное ускорение стационарной голономной системы во все моменты времени пропорционально обобщенной силе с коэффициентом пропорциональности равным обратному коэффициенту инерции системы. В случае консервативной системы, когда все приложенные активные силы потенциальны, уравнение (3) принимает вид:

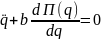
где П(q) – потенциальная энергия системы приложенных сил.выраженная

через обобщенную координату.