
- •«Санкт-петербургский государственный университет технологии и дизайна»
- •Тема 1.
- •Тема 2.
- •Тема 3.
- •Тема 4. Основные теоремы теории вероятностей
- •Тема 5.
- •Тема 6. Числовые характеристики дискретных случайных величин.
- •Тема 7. Функция распределения и плотность распределения вероятностей непрерывной случайной величины
- •Тема 8. Нормальный закон распределения
- •Тема 9. Уравнение регрессии.
- •X-Coordinates
- •Variance
- •Intercept
Тема 6. Числовые характеристики дискретных случайных величин.
Математическое ожидание дискретной
случайной величины
![]() ,
имеющей конечное число возможных
значений, равно
,
имеющей конечное число возможных
значений, равно
![]() ,
(1).
,
(1).
Математическое ожидание дискретной
случайной величины
![]() ,
имеющей бесконечное число возможных
значений, равно
,
имеющей бесконечное число возможных
значений, равно
![]() ,
(2).
,
(2).
Причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
В формулах (1) и (2):
![]() - возможные значения случайной величины
- возможные значения случайной величины![]() ,
,![]() - вероятности того, что случайная величина
- вероятности того, что случайная величина![]() примет эти значения.
примет эти значения.
Свойства математического ожидания:
1.
![]() (3).
(3).
Где
![]() -
постоянная величина.
-
постоянная величина.
2.
![]() ,
(4).
,
(4).
Где
![]() =const.
=const.
3.
![]() (5).
(5).
Где
![]() и
и![]() - две любые случайные величины.
- две любые случайные величины.
4.
![]() ,
(6).
,
(6).
Где
![]() и
и![]() - две независимые случайные величины.
- две независимые случайные величины.
Дисперсия случайной величины определяется равенством
![]() ,
(7)
,
(7)
Или равносильным ему равенством
![]() (8).
(8).
Дисперсию дискретной случайной величины, имеющей конечное число возможных значений, можно вычислять по формуле
![]() ,
(9).
,
(9).
Соответствующей формуле (7), или по формуле
![]() , (10),
, (10),
соответствующей формуле (8).
Свойства дисперсии:
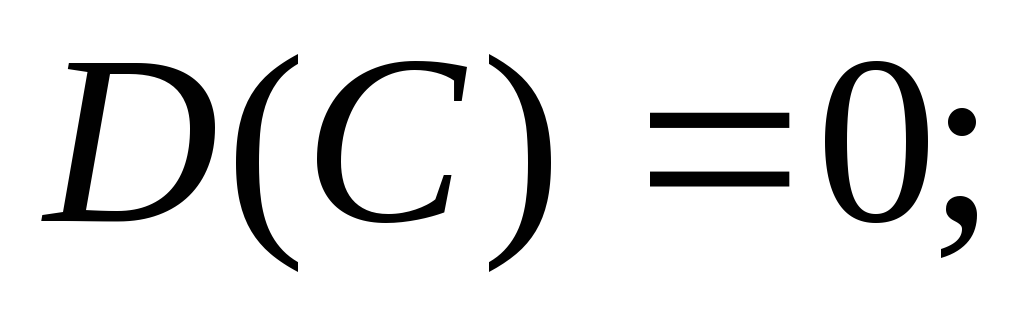 (11)
(11)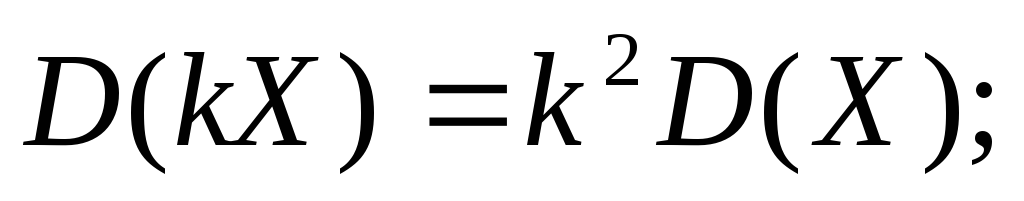 (12)
(12)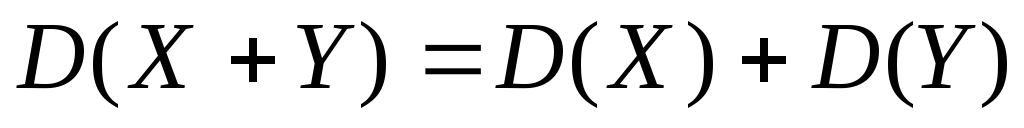 ;
(13), где
;
(13), где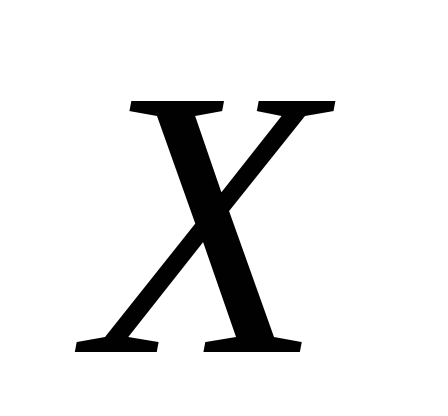 и
и - две независимые случайные величины.
- две независимые случайные величины.
Среднее квадратическое отклонение
случайной величины
![]() равно
равно
![]() (14).
(14).
Задача образец
Дискретная случайная величина
![]() задана рядом распределения
задана рядом распределения

Найти ее математическое ожидание, дисперсию и среднее квадратическое отклонение.
Ответ:
![]() ;
;![]() ;
;![]()
определяем
количество переменных, для того
чтобы
сделать 1..3 надо нажать ":"
для
того, чтобы получить xi
надо
нажать "[",
и
для того, чтобы вставить данные в столбец
надо нажимать
",".
![]()
![]()
![]()
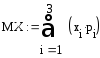
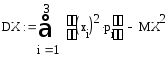
![]()
![]()
![]()
![]()
Задача № 2
В результате обработки данных многолетних
наблюдений получены распределения
случайных величин
![]() и
и![]() числа
хозяйств в каждом из двух районов
области, которых урожайность зерновых
культур может превысить 35 ц/га.
числа
хозяйств в каждом из двух районов
области, которых урожайность зерновых
культур может превысить 35 ц/га.
Для первого района области:
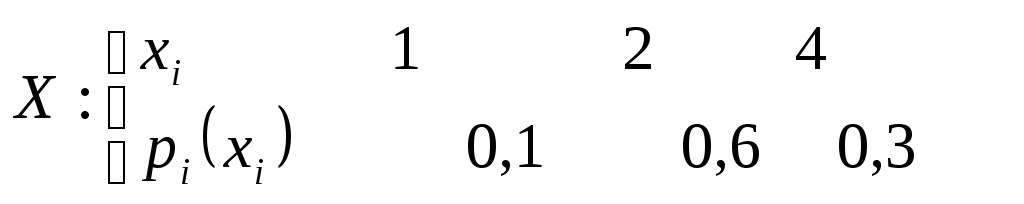 .
.
Для второго района области:
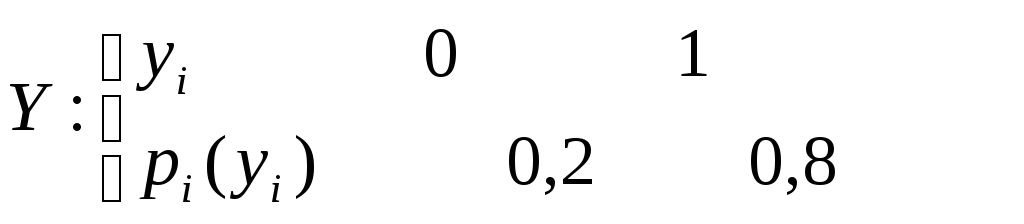 .
.
Найти математическое ожидание
![]() и дисперсию
и дисперсию![]() случайной величины
случайной величины![]() двумя
способами:
двумя
способами:
А) исходя из закона распределения
![]() ;
;
Б) используя свойства математического ожидания и дисперсию, отраженные формулами (5) и (13).
Убедиться в том, что в условиях данной задачи эти свойства независимых случайных величин выполняются.
Ответ:
![]() ;
;![]() .
.
Указание: надо найти все возможные
значения случайной величины
![]() и вероятности
и вероятности![]() этих значений. Для этого надо учесть
следующее, что суммой (разностью или
произведением) случайных величин
этих значений. Для этого надо учесть
следующее, что суммой (разностью или
произведением) случайных величин![]() и
и![]() называется случайная величина , которая
принимает все возможные значения вида
называется случайная величина , которая
принимает все возможные значения вида![]() (
(![]() или
или![]() ),
где
),
где![]() с вероятностями
с вероятностями![]() того, что случайная величина
того, что случайная величина![]() примет
значение
примет
значение![]() ,
а
,
а![]() - значение
- значение![]() :
:
![]() .
.
Если случайные величины
![]() и
и![]() независимы, то по теореме умножения
вероятностей независимых событий
независимы, то по теореме умножения
вероятностей независимых событий
![]() .
.
Для конкретного примера:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() .
.
Для расчета вероятностей удобно составить следующую таблицу:
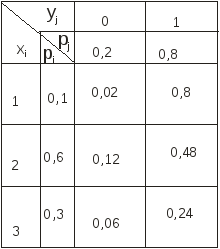
Получим следующий ряд распределения
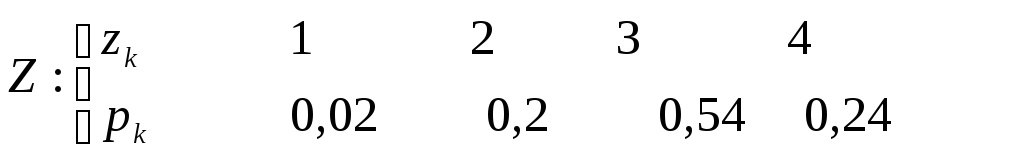
Далее необходимо рассчитать
![]() и
и![]() ,
а также
,
а также![]() и убедиться , что справедливы свойства
математического ожидания и дисперсии.
и убедиться , что справедливы свойства
математического ожидания и дисперсии.
Задача № 3.
Найти математическое ожидание случайной
величины
![]() ,
если известны математические ожидания
,
если известны математические ожидания![]() ,
,![]() .
.
Ответ: 31.
Задача № 4.
Доказать, что
![]() .
.
Задача № 5.
Доказать, что для независимых случайных
величин
![]() и
и![]() справедливо равенство:
справедливо равенство:![]() .
.
Задача № 6.
Случайные величины
![]() и
и![]() .
Известны дисперсии этих величин:
.
Известны дисперсии этих величин:![]() .
Найти дисперсию случайной величины
.
Найти дисперсию случайной величины![]() .
.
Ответ: 29.
Задача № 7.
На птицефабрике три терморегулятора
работают независимо друг от друга.
Вероятность бесперебойной работы в
течении смены первого терморегулятора
равна 0,6. для второго и третьего эти
вероятности соответственно равны 0,8 и
0,9. найти закон распределения случайной
величины
![]() - числа терморегуляторов, бесперебойно
работающих в течение смены. Вычислить
математическое ожидание, дисперсию и
среднеквадратическое отклонение
величины
- числа терморегуляторов, бесперебойно
работающих в течение смены. Вычислить
математическое ожидание, дисперсию и
среднеквадратическое отклонение
величины![]() .
.
Ответ:
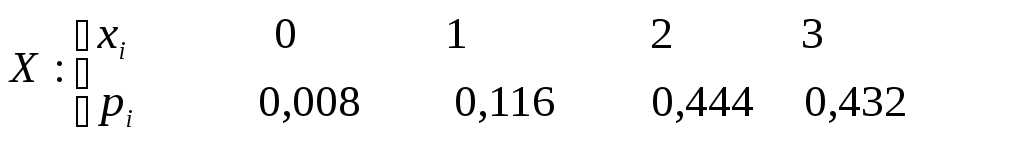
![]() .
.
Указание. Рассмотреть события:
![]() - в течение смены будут бесперебойно
работать соответственно первый, второй,
третий терморегуляторы.
- в течение смены будут бесперебойно
работать соответственно первый, второй,
третий терморегуляторы.
![]() - в течение смены не будут бесперебойно
работать соответственно первый, второй,
третий терморегуляторы.
- в течение смены не будут бесперебойно
работать соответственно первый, второй,
третий терморегуляторы.
![]() - будут сбои в работе трех терморегуляторов;
- будут сбои в работе трех терморегуляторов;
![]() - бесперебойно будет работать один
терморегулятор;
- бесперебойно будет работать один
терморегулятор;
![]() - бесперебойно будут работать два
терморегулятора;
- бесперебойно будут работать два
терморегулятора;
![]() - бесперебойно будут работать три
терморегулятора.
- бесперебойно будут работать три
терморегулятора.
