Matematika_Tipovik_1_semestr_2_modul (1)
.doc
|
|
|
|
4а
Провести полное исследование функции и построить её график:
-
16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.
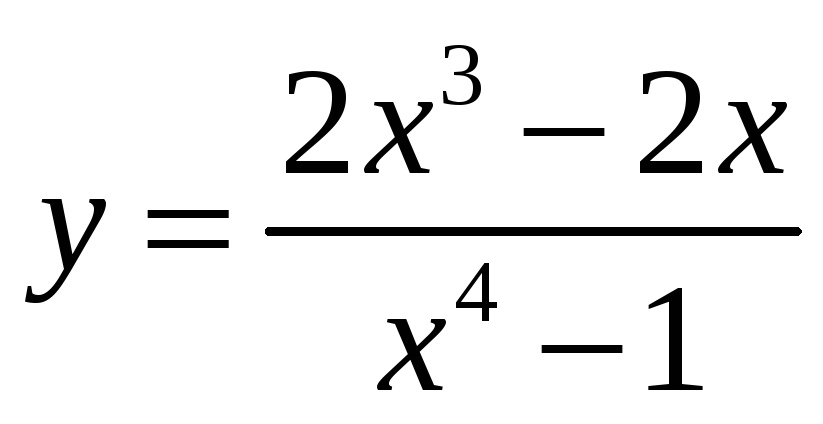
27.

28.

29.

30.

-
4б*
Провести полное исследование функции и построить её график:
|
1.
|
16.
|
|
2.
|
17.
|
|
3.
|
18.
|
|
4.
|
19.
|
|
5.
|
20.
|
|
6.
|
21.
|
|
7.
|
22.
|
|
8.
|
23.
|
|
9.
|
24.
|
|
10.
|
25.
|
|
11.
|
26.
|
|
12.
|
27.
|
|
13.
|
28.
|
|
14.
|
29.
|
|
15.
|
30.
|
5а
-
Известно, что сумма двух положительных чисел
 и
и
 равна 15. При каких значениях
равна 15. При каких значениях
 и
и
 величина
величина
 будет наибольшей?
будет наибольшей? -
Известно, что произведение двух положительных чисел
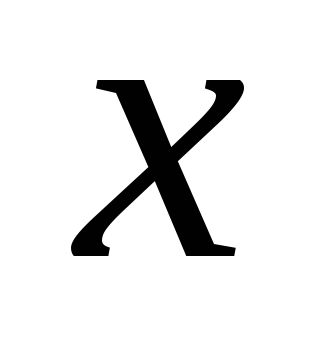 и
и
 равно
16. При каких значениях
равно
16. При каких значениях
 и
и
 их сумма будет наименьшей?
их сумма будет наименьшей? -
Для двух положительных чисел
 и
и
 известно, что
известно, что
 .
При каких значениях
.
При каких значениях
 и
и
 их произведение будет наибольшим?
их произведение будет наибольшим? -
Известно, что сумма двух положительных чисел
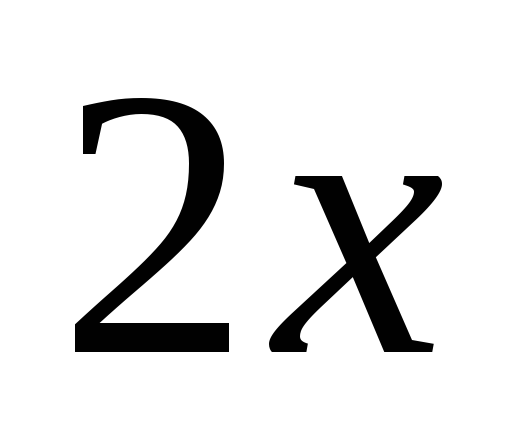 и
и
 равна 15. При каких значениях
равна 15. При каких значениях
 и
и
 величина
величина
 будет наибольшей?
будет наибольшей? -
Известно, что удвоенное произведение двух положительных чисел
 и
и
 равно
18. При каких значениях
равно
18. При каких значениях
 и
и
 их сумма будет наименьшей?
их сумма будет наименьшей? -
Для двух положительных чисел
 и
и
 известно, что
известно, что
 .
При каких значениях
.
При каких значениях
 и
и
 их произведение будет наибольшим?
их произведение будет наибольшим? -
Для двух положительных чисел
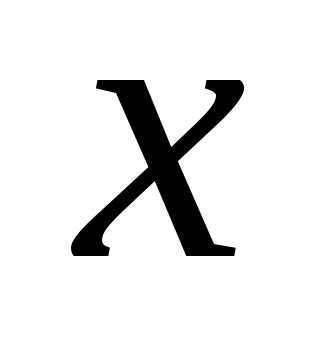 и
и
 известно,
что
известно,
что
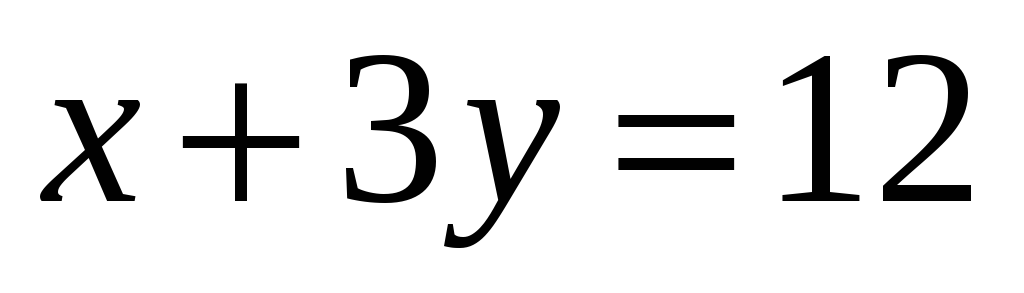 .
При каких значениях
.
При каких значениях
 и
и
 величина
величина
 будет наибольшей?
будет наибольшей? -
Для двух положительных чисел
 и
и
 известно,
что
известно,
что
 .
При каких значениях
.
При каких значениях
 и
и
 величина
величина
 будет наименьшей?
будет наименьшей? -
Для двух положительных чисел
 и
и
 известно, что
известно, что
 .
При каких значениях
.
При каких значениях
 и
и
 величина
величина
 будет наибольшей?
будет наибольшей? -
Для двух положительных чисел
 и
и
 известно,
что
известно,
что
 .
При каких значениях
.
При каких значениях
 и
и
 величина
величина
 будет наибольшей?
будет наибольшей? -
Для двух положительных чисел
 и
и
 известно,
что
известно,
что
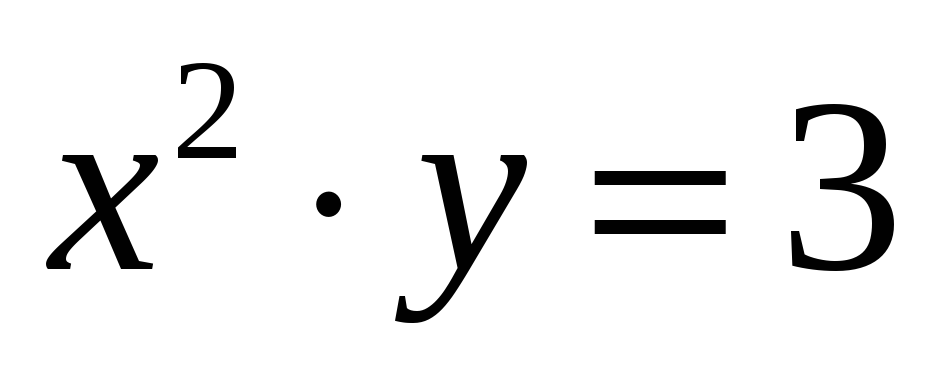 .
При каких значениях
.
При каких значениях
 и
и
 величина
величина
 будет наименьшей?
будет наименьшей? -
Для двух положительных чисел
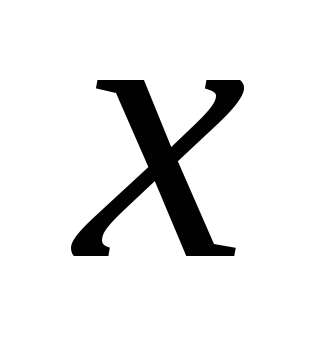 и
и
 известно, что
известно, что
 .
При каких значениях
.
При каких значениях
 и
и
 величина
величина
 будет наибольшей?
будет наибольшей? -
Для двух положительных чисел
 и
и
 известно,
что
известно,
что
 . При каких значениях
. При каких значениях
 и
и
 величина
величина
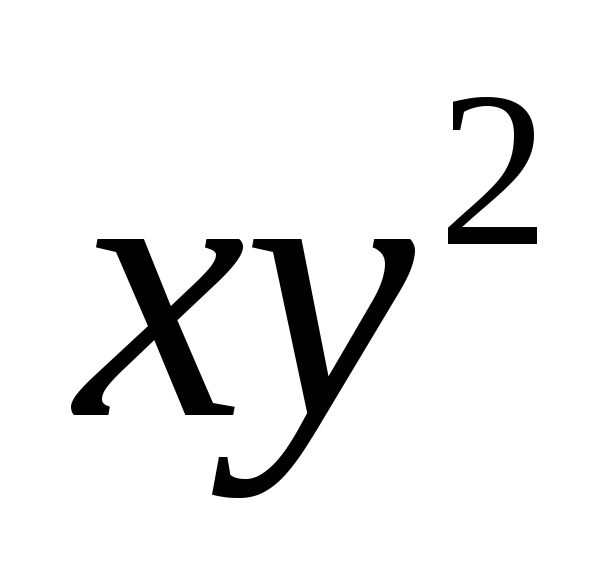 будет наибольшей?
будет наибольшей? -
Для двух положительных чисел
 и
и
 известно,
что
известно,
что
 .
При каких значениях
.
При каких значениях
 и
и
 величина
величина
 будет наименьшей?
будет наименьшей? -
Для двух положительных чисел
 и
и
 известно, что
известно, что
 .
При каких значениях
.
При каких значениях
 и
и
 величина
величина
 будет наибольшей?
будет наибольшей? -
Известно, что сумма двух положительных чисел
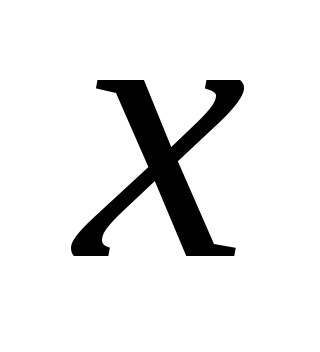 и
и
 равна 21. При каких значениях
равна 21. При каких значениях
 и
и
 величина
величина
 будет наибольшей?
будет наибольшей? -
Известно, что произведение двух положительных чисел
 и
и
 равно
25. При каких значениях
равно
25. При каких значениях
 и
и
 их сумма будет наименьшей?
их сумма будет наименьшей? -
Для двух положительных чисел
 и
и
 известно, что
известно, что
 .
При каких значениях
.
При каких значениях
 и
и
 их произведение будет наибольшим?
их произведение будет наибольшим? -
Для двух положительных чисел
 и
и
 известно, что
известно, что
 .
При каких значениях
.
При каких значениях
 и
и
 величина
величина
 будет наибольшей?
будет наибольшей? -
Для двух положительных чисел
 и
и
 известно,
что
известно,
что
 .
При каких значениях
.
При каких значениях
 и
и
 величина
величина
 будет наименьшей?
будет наименьшей? -
Для двух положительных чисел
 и
и
 известно, что
известно, что
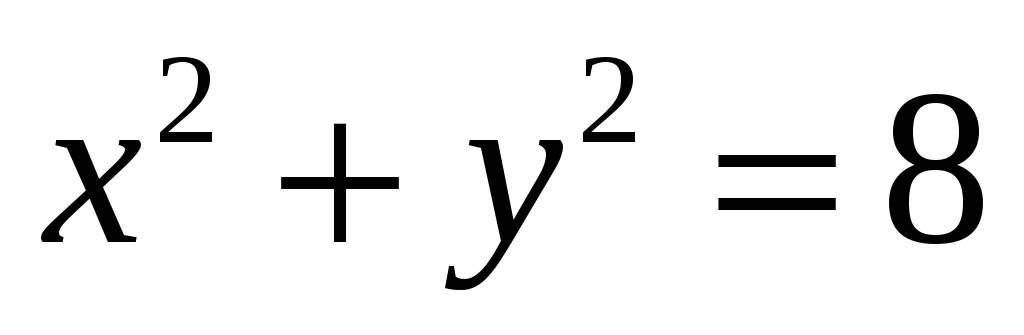 .
При каких значениях
.
При каких значениях
 и
и
 их произведение будет наибольшим?
их произведение будет наибольшим? -
Для двух положительных чисел
 и
и
 известно,
что
известно,
что
 .
При каких значениях
.
При каких значениях
 и
и
 величина
величина
 будет наибольшей?
будет наибольшей? -
Для двух положительных чисел
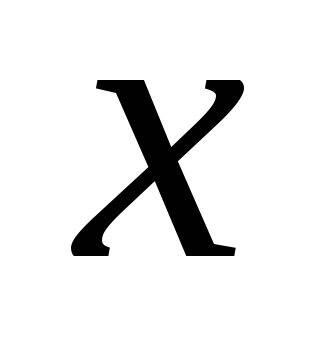 и
и
 известно,
что
известно,
что
 .
При каких значениях
.
При каких значениях
 и
и
 величина
величина
 будет наименьшей?
будет наименьшей? -
Для двух положительных чисел
 и
и
 известно, что
известно, что
 .
При каких значениях
.
При каких значениях
 и
и
 величина
величина
 будет наибольшей?
будет наибольшей? -
Для двух положительных чисел
 и
и
 известно,
что
известно,
что
 .
При каких значениях
.
При каких значениях
 и
и
 величина
величина
 будет наибольшей?
будет наибольшей? -
Для двух положительных чисел
 и
и
 известно,
что
известно,
что
 .
При каких значениях
.
При каких значениях
 и
и
 величина
величина
 будет наименьшей?
будет наименьшей? -
Для двух положительных чисел
 и
и
 известно, что
известно, что
 .
При каких значениях
.
При каких значениях
 и
и
 величина
величина
 будет наибольшей?
будет наибольшей? -
Для двух положительных чисел
 и
и
 известно,
что
известно,
что
 .
При каких значениях
.
При каких значениях
 и
и
 величина
величина
 будет наибольшей?
будет наибольшей? -
Для двух положительных чисел
 и
и
 известно,
что
известно,
что
 .
При каких значениях
.
При каких значениях
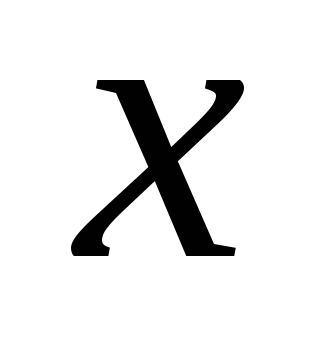 и
и
 величина
величина
 будет наименьшей?
будет наименьшей? -
Для двух положительных чисел
 и
и
 известно, что
известно, что
 .
При каких значениях
.
При каких значениях
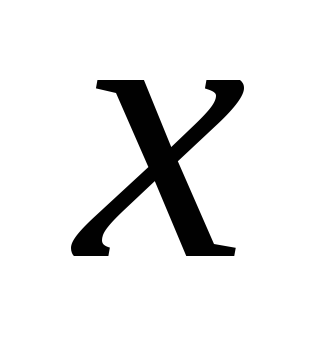 и
и
 величина
величина
 будет наибольшей?
будет наибольшей?
5 б*
Определить наибольшее отклонение от нуля функции на отрезке:
|
|
|
17.
|
|
18.
|
|
19.
|
|
20.
|
|
21.
|
|
22.
|
|
23.
|
|
24.
|
|
25.
|
|
26.
|
|
27.
|
|
28.
|
|
29.
|
|
30.
|
5в*
-
В прямой круговой конус с углом
 в осевом сечении и радиусом основания
в осевом сечении и радиусом основания
 вписан цилиндр. Определить радиус
основания и высоту цилиндра, при которых
его полная поверхность будет наибольшей.
вписан цилиндр. Определить радиус
основания и высоту цилиндра, при которых
его полная поверхность будет наибольшей. -
Найти наибольшее значение площади прямоугольного треугольника АВС, в котором угол С прямой, если одной вершиной является точка А(0;0), вершина В лежит на графике функции
 ,
а вершина С
расположена на оси абсцисс и её абсцисса
удовлетворяет соотношению
,
а вершина С
расположена на оси абсцисс и её абсцисса
удовлетворяет соотношению

-
Определить радиус цилиндра, вписанного в шар радиуса
 ,
который имеет наибольшую боковую
поверхность. Указать значение площади
полной поверхности такого цилиндра.
,
который имеет наибольшую боковую
поверхность. Указать значение площади
полной поверхности такого цилиндра. -
При подготовке к экзамену студент за
 дней изучает
дней изучает
 -ую
часть курса, а забывает
-ую
часть курса, а забывает
 -ую
часть. Сколько дней надо затратить на
подготовку, чтобы была изучена
максимальная часть курса, если
-ую
часть. Сколько дней надо затратить на
подготовку, чтобы была изучена
максимальная часть курса, если
 и
и
 ?
? -
Найти радиус основания конуса с заданной площадью боковой поверхности
 ,
который имеет наибольший объём.
,
который имеет наибольший объём. -
Криволинейная трапеция ограничена кривой
 и отрезками прямых
и отрезками прямых

 .
В какой точке кривой следует провести
касательную, чтобы она отсекала от
криволинейной трапеции обычную трапецию
наибольшей площади? Указать значение
этой площади.
.
В какой точке кривой следует провести
касательную, чтобы она отсекала от
криволинейной трапеции обычную трапецию
наибольшей площади? Указать значение
этой площади. -
Найти радиус основания и высоту цилиндра, вписанного в конус с высотой
 и радиусом
и радиусом
 ,
боковая поверхность которого будет
наибольшей.
,
боковая поверхность которого будет
наибольшей.
-
В пространстве задана стандартная прямоугольная система координат
 .
Нужно пройти кратчайшим путем от точки
.
Нужно пройти кратчайшим путем от точки
 до точки
до точки
 ,
обязательно заходя по пути на ось
,
обязательно заходя по пути на ось
 .
Определить длину такого кратчайшего
пути.
.
Определить длину такого кратчайшего
пути. -
Найти размеры правильной треугольной пирамиды заданного объёма
 ,
которая имеет наименьшую сумму рёбер.
,
которая имеет наименьшую сумму рёбер. -
Провести через заданную точку
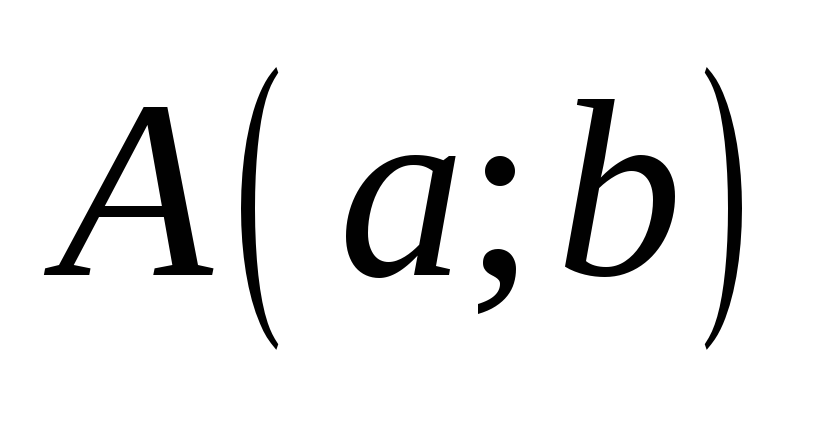 ,
лежащую внутри некоторого угла
,
лежащую внутри некоторого угла
 ,
прямую, которая отсечёт от этого угла
треугольник наименьшей площади. Указать
значение этой площади.
,
прямую, которая отсечёт от этого угла
треугольник наименьшей площади. Указать
значение этой площади. -
По двум прямолинейным дорогам, составляющим угол в
 ,
в направлении их пересечения одновременно
начинают двигаться два пешехода: один
со скоростью
,
в направлении их пересечения одновременно
начинают двигаться два пешехода: один
со скоростью
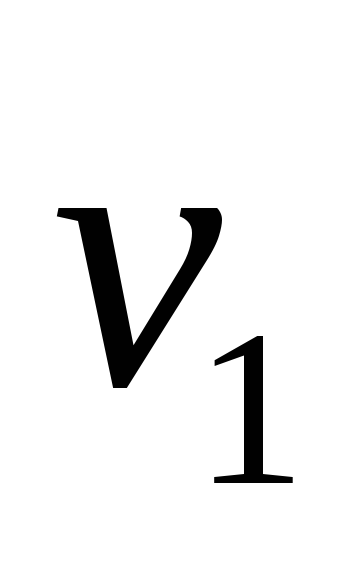 км/ч, а другой -
км/ч, а другой -
 км/ч. В начальный момент первый пешеход
находится на расстоянии
км/ч. В начальный момент первый пешеход
находится на расстоянии
 км от перекрестка, а другой на расстоянии
км от перекрестка, а другой на расстоянии
 км. Через какое время после начала
движения расстояние между ними будет
наименьшим? Определить это расстояние.
км. Через какое время после начала
движения расстояние между ними будет
наименьшим? Определить это расстояние. -
Найти наибольшее возможное значение отношения объёма конуса, вписанного в шар радиуса
 ,
к объёму шара. Определить расстояние
от центра шара до основания конуса.
,
к объёму шара. Определить расстояние
от центра шара до основания конуса. -
В прямоугольник
 со сторонами 24 и 27 см вписаны две
касающиеся друг друга окружности. Одна
окружность касается сторон
со сторонами 24 и 27 см вписаны две
касающиеся друг друга окружности. Одна
окружность касается сторон
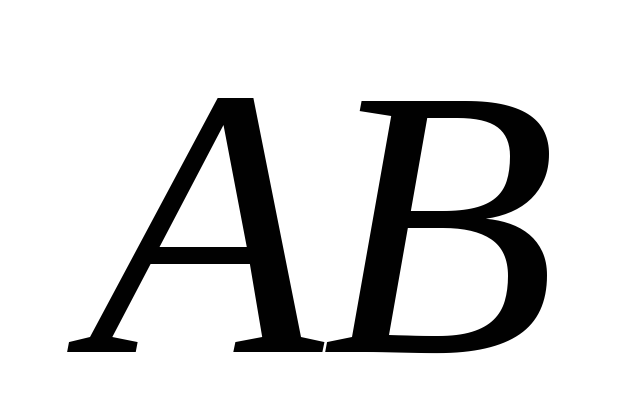 и
и
 ,
а другая – сторон
,
а другая – сторон
 и
и
 .
Найти наименьшее значение суммы
площадей, ограниченных этими окружностями.
.
Найти наименьшее значение суммы
площадей, ограниченных этими окружностями. -
Проволокой длины
 необходимо огородить клумбу, имеющую
форму кругового сектора. Найти радиус
круга, при котором площадь клумбы будет
наибольшей.
необходимо огородить клумбу, имеющую
форму кругового сектора. Найти радиус
круга, при котором площадь клумбы будет
наибольшей. -
В треугольнике
 на сторонах
на сторонах
 и
и
 взяты точки
взяты точки
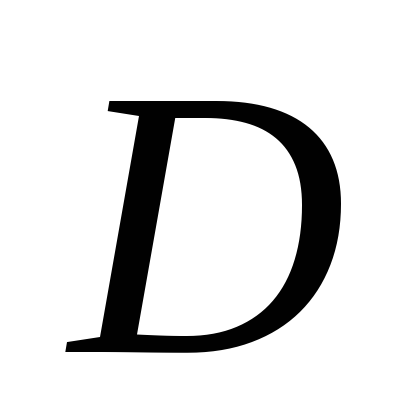 и
и
 соответственно так, что прямая
соответственно так, что прямая
 параллельна стороне
параллельна стороне
 .
Точка
.
Точка
 делит сторону
делит сторону
 на части так, что
на части так, что
 .
Площадь треугольника
.
Площадь треугольника
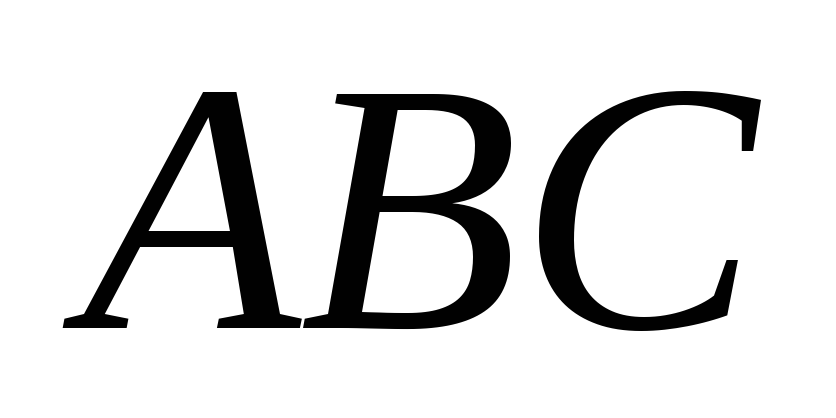 равна 1. Определить значение
равна 1. Определить значение
 ,
чтобы площадь трапеции
,
чтобы площадь трапеции
 была наибольшей.
была наибольшей. -
Найти радиус и высоту цилиндра, имеющего наибольший объём, который вписан в куб с ребром
 так, что его ось совпадает с диагональю
куба, а окружности оснований касаются
граней куба.
так, что его ось совпадает с диагональю
куба, а окружности оснований касаются
граней куба. -
Вершинами треугольника
 являются точки
являются точки
 и
и
 ,
а третья вершина
,
а третья вершина
 лежит на параболе
лежит на параболе
 .
Найти наименьшее возможное значение
площади такого треугольника.
.
Найти наименьшее возможное значение
площади такого треугольника. -
Определить высоту конуса, вписанного в шар радиуса
 ,
который имеет наибольшую площадь полной
поверхности. Указать значение площади
полной поверхности такого конуса.
,
который имеет наибольшую площадь полной
поверхности. Указать значение площади
полной поверхности такого конуса. -
В какой точке с абсциссой
 графика функции
графика функции
 следует провести касательную, чтобы
площадь фигуры, ограниченной графиком,
касательной и прямой
следует провести касательную, чтобы
площадь фигуры, ограниченной графиком,
касательной и прямой
 была наименьшей?
была наименьшей? -
Определить наибольшую площадь прямоугольника, вписанного симметрично в сектор круга радиуса
 с центральным углом
с центральным углом
 .
. -
В прямоугольном круговом конусе произведение высоты и радиуса основания равны
 .
Какое наименьшее значение может
принимать радиус шара, описанного
вокруг этого конуса?
.
Какое наименьшее значение может
принимать радиус шара, описанного
вокруг этого конуса? -
Найти наибольший объём правильного параллелепипеда, который можно вписать в эллипсоид вращения

-
Определить высоту конуса, описанного около полушара радиуса
 ,
который имеет наименьший объём, если
его основание и основание полушара
лежат в одной плоскости и концентричны.
,
который имеет наименьший объём, если
его основание и основание полушара
лежат в одной плоскости и концентричны. -
На координатной плоскости
 задано множество всех равносторонних
треугольников, две вершины которых
лежат на прямой
задано множество всех равносторонних
треугольников, две вершины которых
лежат на прямой
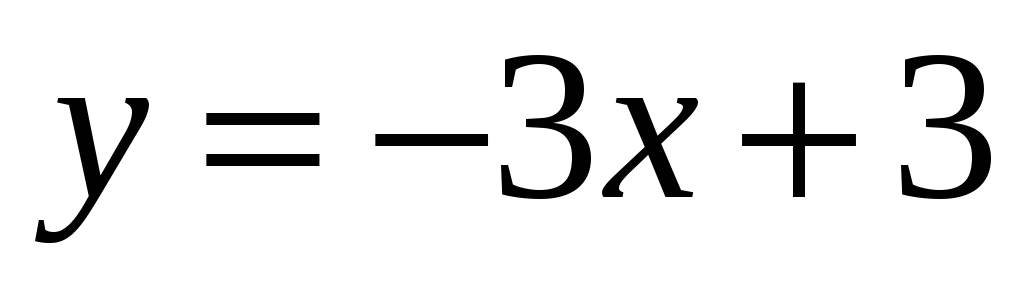 ,
а координаты третьей вершины удовлетворяют
неравенству
,
а координаты третьей вершины удовлетворяют
неравенству
 .
Найти наибольшее возможное значение
площади таких треугольников.
.
Найти наибольшее возможное значение
площади таких треугольников. -
В сферу вписаны правильная треугольная пирамида со стороной основания 9 и правильная четырехугольная призма, нижние плоскости оснований которых совпадают. Центр сферы делит высоту призмы в отношении
 ,
считая от вершины. Найти наибольшее
возможное значение объёма призмы.
,
считая от вершины. Найти наибольшее
возможное значение объёма призмы. -
Провести через заданную точку
 ,
лежащую внутри некоторого угла
,
лежащую внутри некоторого угла
 ,
прямую, которая отсечёт от этого угла
два отрезка, суммарная длина которых
будет наименьшей. Указать значение
этой суммы.
,
прямую, которая отсечёт от этого угла
два отрезка, суммарная длина которых
будет наименьшей. Указать значение
этой суммы. -
Из фигуры, ограниченной кривой
 и прямыми
и прямыми
 и
и
 нужно
вырезать прямоугольник наибольшей
площади. Определить стороны этого
прямоугольника.
нужно
вырезать прямоугольник наибольшей
площади. Определить стороны этого
прямоугольника. -
Найти кратчайшее расстояние между кривыми
 и
и
 ,
,
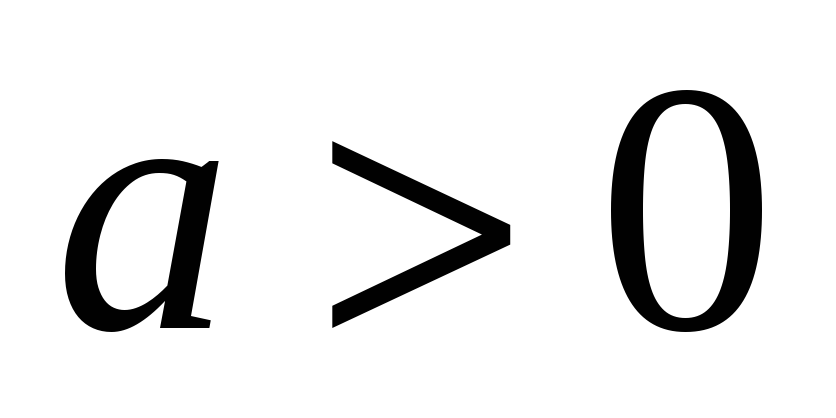 .
. -
В треугольной пирамиде
 расстояние
от каждой из вершин до середины ребра
расстояние
от каждой из вершин до середины ребра
 равны
равны
 см. При какой величине двугранного угла
при ребре
см. При какой величине двугранного угла
при ребре
 объём пирамиды будет наибольшим? Найти
этот объём.
объём пирамиды будет наибольшим? Найти
этот объём. -
В какой точке с абсциссой
 графика функции
графика функции
 следует провести касательную, чтобы
площадь фигуры, ограниченной графиком,
касательной и прямой
следует провести касательную, чтобы
площадь фигуры, ограниченной графиком,
касательной и прямой
 была наименьшей?
была наименьшей?